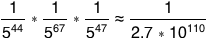
What would happen if you tried to hit a baseball pitched at 90% the speed of light?
- Ellen McManis
Let’s set aside the question of how we got the baseball moving that fast. We'll suppose it's a normal pitch, except in the instant the pitcher releases the ball, it magically accelerates to 0.9c. From that point onward, everything proceeds according to normal physics.:
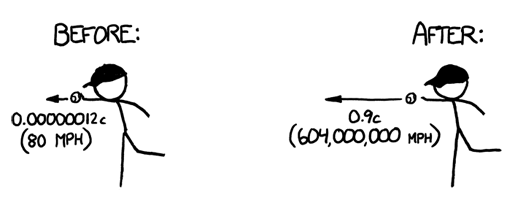
pitcher throwing ball
The answer turns out to be “a lot of things”, and they all happen very quickly, and it doesn’t end well for the batter (or the pitcher). I sat down with some physics books, a Nolan Ryan action figure, and a bunch of videotapes of nuclear tests and tried to sort it all out. What follows is my best guess at a nanosecond-by-nanosecond portrait:
The ball is going so fast that everything else is practically stationary. Even the molecules in the air are stationary. Air molecules vibrate back and forth at a few hundred miles per hour, but the ball is moving through them at 600 million miles per hour. This means that as far as the ball is concerned, they’re just hanging there, frozen.
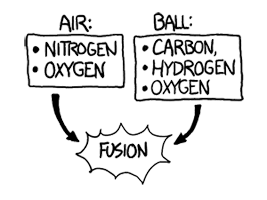
The ideas of aerodynamics don’t apply here. Normally, air would flow around anything moving through it. But the air molecules in front of this ball don’t have time to be jostled out of the way. The ball smacks into them so hard that the atoms in the air molecules actually fuse with the atoms in the ball’s surface. Each collision releases a burst of gamma rays and scattered particles.
fusion illustration
fusion zone of baseball
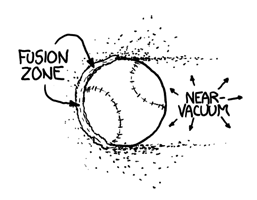
These gamma rays and debris expand outward in a bubble centered on the pitcher’s mound. They start to tear apart the molecules in the air, ripping the electrons from the nuclei and turning the air in the stadium into an expanding bubble of incandescent plasma. The wall of this bubble approaches the batter at about the speed of light—only slightly ahead of the ball itself.
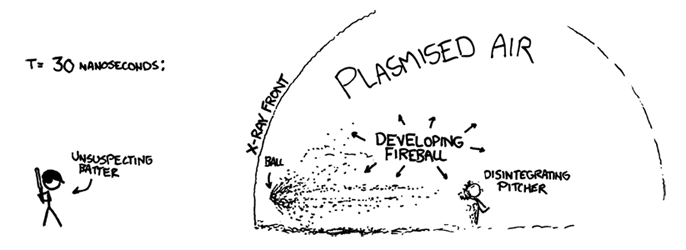
t=30 nanoseconds
The constant fusion at the front of the ball pushes back on it, slowing it down, as if the ball were a rocket flying tail-first while firing its engines. Unfortunately, the ball is going so fast that even the tremendous force from this ongoing thermonuclear explosion barely slows it down at all. It does, however, start to eat away at the surface, blasting tiny particulate fragments of the ball in all directions. These fragments are going so fast that when they hit air molecules, they trigger two or three more rounds of fusion.
After about 70 nanoseconds the ball arrives at home plate. The batter hasn't even seen the pitcher let go of the ball, since the light carrying that information arrives at about the same time the ball does. Collisions with the air have eaten the ball away almost completely, and it is now a bullet-shaped cloud of expanding plasma (mainly carbon, oxygen, hydrogen, and nitrogen) ramming into the air and triggering more fusion as it goes. The shell of x-rays hits the batter first, and a handful of nanoseconds later the debris cloud hits.
When it reaches the batter, the center of the cloud is still moving at an appreciable fraction of the speed of light. It hits the bat first, but then the batter, plate, and catcher are all scooped up and carried backward through the backstop as they disintegrate. The shell of x-rays and superheated plasma expands outward and upward, swallowing the backstop, both teams, the stands, and the surrounding neighborhood—all in the first microsecond.
Suppose you’re watching from a hilltop outside the city. The first thing you see is a blinding light, far outshining the sun. This gradually fades over the course of a few seconds, and a growing fireball rises into a mushroom cloud. Then, with a great roar, the blast wave arrives, tearing up trees and shredding houses.
Everything within roughly a mile of the park is leveled, and a firestorm engulfs the surrounding city. The baseball diamond is now a sizable crater, centered a few hundred feet behind the former location of the backstop.

mushroom cloud
A careful reading of official Major League Baseball Rule 6.08(b) suggests that in this situation, the batter would be considered "hit by pitch", and would be eligible to advance to first base.
i like you marion
What if everyone who took the SAT guessed on every multiple-choice question? How many perfect scores would there be?
—Rob Balder
None.
The SAT is a standardized test given to high school students (similar to the ACT). The scoring is such that under certain circumstances, guessing an answer can be a good strategy. But what if you guessed on everything?
Not all of the SAT is multiple-choice, so let’s focus on the multiple choice questions to keep things simple. We’ll assume everyone gets the essay questions and fill-in-the-number sections correct.
There are 44 multiple-choice questions in the math (quantitative) section, 67 in the critical reading (qualitative) section, and 47 in the newfangled writing section. Each question has five options, so a random guess has a 20% chance of being right:

multiple choice question bubbles
Although we all know the answer is always B.
The probability of getting all 158 questions is: 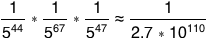
(That's one in twenty-seven quinquatrigintillion.)
If all four million 17-year-olds all took the SAT, and they all guessed randomly, it’s a statistical certainty that there would be no perfect scores on any of the three sections.
How certain is it? Well, if they each used a computer to take the test a million times each day, and continued this every day for five billion years—until the Sun expanded to a red giant and the Earth was charred to a cinder—the chance of any of them ever getting a perfect score on just the math section would be about 0.0001%.
How unlikely is that? Each year something like 500 Americans are struck by lightning[Cooper, Mary Ann, MD. "Disability, Not Death is the Main Problem with Lightning Injury"][http://www.nws.noaa.gov/om/hazstats/light08.pdf] (based on an average of 45 lightning deaths and a 9-10% fatality rate). This suggests that the odds of any one American being hit in a given year are about one in in 700,000 (although probability can be tricky).
This means that the odds of acing the SAT by guessing are worse than the odds of every living ex-President and every member of the main cast of Firefly all being independently struck by lightning … on the same day.
lightning strikes
(Everyone survives but Alan Tudyk and Ron Glass)
To everyone taking the SAT this year, good luck—but it won’t be enough.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
How much Force power can Yoda output?
—Ryan Finnie

Yoda controlling four wind turbines
I’m going to—of course—ignore the prequels.
There’s a great SMBC comic exploring the geopolitical consequences of having Superman turn a crank to provide an unlimited source of energy. We could imagine Yoda using the Force to run a similar generator. But how much power could he really supply?
Yoda’s greatest display of raw power in the original trilogy came when he lifted Luke’s X-Wing from the swamp. As far as physically moving objects around goes, this was easily the biggest expenditure of energy through the Force we saw from anyone in the trilogy.
The energy it takes to lift an object to height h is equal to the object’s mass times the force of gravity times the height it’s lifted. The X-Wing scene lets us use this to put a lower limit on Yoda's peak power output.
First we need to know how heavy the ship was. The X-Wing’s mass has never been canonically established, but its length has—12.5 meters. An F-22 is 19 meters long and weighs 19,700 kg, so scaling down from this gives an estimate for the X-Wing of about 12,000 lbs (5 metric tons).
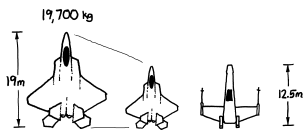
illustration of an X-Wing and F-22
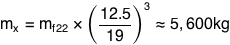
Next, we need to know how fast it was rising. I went over footage of the scene and timed the X-Wing's rate of ascent as it was emerging from the water.

character watching star wars for scientific research
The front landing strut rises out of the water in about three and a half seconds, and I estimated the strut to be 1.4 meters long (based on a scene in A New Hope where a crew member squeezes past it), which tells us the X-Wing was rising at 0.39 m/s.
Lastly, we need to know the strength of gravity on Dagobah. Here, I figure I’m stuck, because while sci-fi fans are obsessive, it’s not like there’s gonna be a catalog of minor geophysical characteristics for every planet visited in Star Wars. Right?
Nope. I’ve underestimated the fandom. Wookieepeedia has just such a catalog, and informs us that the surface gravity on Dagobah is 0.9g. Combining this with the X-Wing mass and lift rate gives us our peak power output:
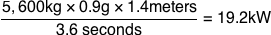
That’s enough to power a block of suburban homes. It’s also equal to about 25 horsepower, which is about the power of the motor in the electric-model Smart Car.
yoda in the engine block of a Smart Car
At current electricity prices, Yoda would be worth about $2/hour.
But telekinesis is just one type of Force power. What about that lightning the Emperor used to zap Luke? The physical nature of it is never made clear, but Tesla coils that produce similar displays draw something like 10 kilowatts—which would put the Emperor roughly on par with Yoda. (Those Tesla coils use lots of very short pulses. If the Emperor is sustaining a continuous arc, as in an arc welder, the power could easily be in the megawatts.)
What about Luke? I examined the scene where he used his nascent Force powers to yank his lightsaber out of the snow. The numbers are harder to estimate here, but I went through frame-by-frame and came up with an estimate of 400 watts for his peak output. This is a fraction of Yoda's 19kW, and was sustained for only a fraction of a second.
So Yoda sounds like our best bet as an energy source. But with world electricity consumption pushing 2 terawatts, it would take a hundred million Yodas to meet our demands. All things considered, switching to Yoda Power probably isn’t worth the trouble—though it would definitely be green.

Yoda controlling and listening to an mp3 player with the force
the first time i saw you, i thought you looked cool (and "fresh" i remember, but i have no idea what i meant exactly with that)
What would happen if you were to gather a mole (unit of measurement) of moles (the small furry critter) in one place?
—Sean Rice
Things get a bit gruesome.
First, some definitions. A mole is a unit. It’s not a typical unit,
though. It’s really just a number—like “dozen” or “billion.” If you have
a mole of something, it means you have 602,214,129,000,000,000,000,000
of them (usually written 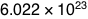 ). It’s such a big
number because it’s used for counting numbers of molecules, which there
are a lot of.
). It’s such a big
number because it’s used for counting numbers of molecules, which there
are a lot of.

a figure with a hand overflowing with molecules
"One mole" is close to the number of atoms in a gram of hydrogen. It’s also, by chance, a decent ballpark guess for the number of grains of sand on Earth.
A mole is also a type of burrowing mammal. There are a handful of types of moles, and some of them are truly horrifying.

a figure searching for, finding, and being scarred by a truly horrrifying star-nosed mole on wikipedia
So what would a mole of moles—602,214,129,000,000,000,000,000 animals—look like?
First, let’s start with wild ballpark approximations. This is an example of what might go through my head before I even pick up a calculator, when I’m just trying to get a sense of the quantities - the kind of calculation where 10, 1, and 0.1 are all close enough that we can consider them equal:
I can pick up a mole (animal) and throw it.[citation needed] Anything I can throw weighs one pound. One pound is one kilogram. The number 602,214,129,000,000,000,000,000 looks about twice as long as a trillion, which means it’s about a trillion trillion. I happen to remember that a trillion trillion kilograms is how much a planet weighs.
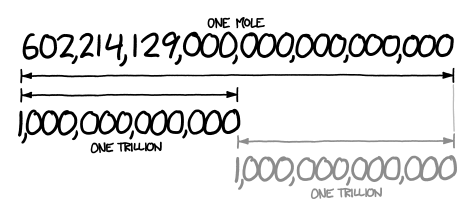
illustration showing that a trillion is visually approximately one half of one mole
… if anyone asks, I did not tell you it was ok to do math like this.
That’s enough to tell us that we’re talking about pile of moles on the scale of planets. It’s a pretty rough estimate, though, since it could be off by a factor of thousands in either direction.
Let’s get some better numbers.
An eastern mole (Scalopus aquaticus) weighs about 75 grams, which means a mole of moles weighs
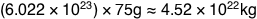
That’s a little over half the mass of our moon.
Mammals are largely water. A kilogram of water takes up a liter of
volume, so if the moles weigh 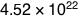 kilograms,
they take up about
kilograms,
they take up about 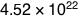 liters of volume. You
might notice that we’re ignoring the pockets of space between the moles.
In a moment, you’ll see why.
liters of volume. You
might notice that we’re ignoring the pockets of space between the moles.
In a moment, you’ll see why.
The cube root of 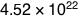 liters is 3,562 kilometers,
which means we’re talking about a sphere with a radius of 2,210
kilometers, or a cube 2,213 miles on each edge. (That’s a neat
coincidence I’ve never noticed before—a cubic mile happens to be almost
exactly
liters is 3,562 kilometers,
which means we’re talking about a sphere with a radius of 2,210
kilometers, or a cube 2,213 miles on each edge. (That’s a neat
coincidence I’ve never noticed before—a cubic mile happens to be almost
exactly 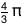 cubic kilometers, so a sphere with a
radius of X kilometers has the same volume as a cube that’s X miles on
each side.)
cubic kilometers, so a sphere with a
radius of X kilometers has the same volume as a cube that’s X miles on
each side.)
If these moles were released onto the Earth’s surface, they’d fill it up to 80 kilometers deep—just about to the (former) edge of space:
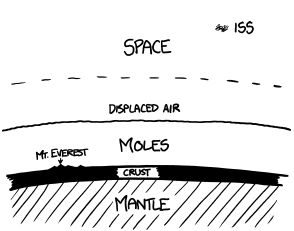
cross section of the earth's surface with 80km of moles between the crust and displaced air before space
This smothering ocean of high-pressure meat would wipe out most life on the planet, which could—to reddit’s horror—threaten the integrity of the DNS system. So doing this on Earth is definitely not an option.
Instead, let’s gather the moles in interplanetary space. Gravitational attraction would pull them into a sphere. Meat doesn’t compress very well, so it would only undergo a little bit of gravitational contraction, and we’d end up with a mole planet a bit larger than the moon.
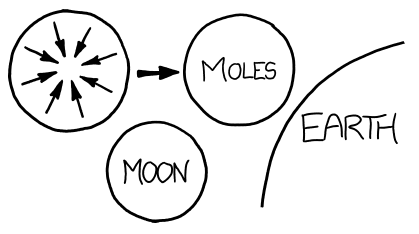
circles showing that a mole of moles makes a sphere slightly larger than our moon
The moles would have a surface gravity about one-sixteenth as strong as Earth’s—similar to that of Pluto. The planet would start off uniformly lukewarm—probably a bit over room temperature—and the gravitational contraction would heat the deep interior by a handful of degrees.
But this is where it gets weird.
The mole planet is now a giant sphere of meat. It has a lot of latent energy (there are enough calories in the mole planet to support the Earth’s current population for 30 billion years). Normally, when organic matter decomposes, it releases much of that energy as heat. But throughout the majority of the planet’s interior, the pressure is over a hundred megapascals, which is enough to kill all bacteria and sterilize the mole remains—leaving no microorganisms to break down the mole tissues.
Closer to the surface, where the pressure is lower, there’s another obstacle to decomposition—the interior of a mole planet is low in oxygen. Without oxygen, the usual decomposition doesn’t happen, and the only bacteria that can break down the moles are those which don’t require oxygen. While inefficient, this anaerobic decomposition can unlock quite a bit of heat. If continued unchecked, it would heat the planet to a boil.
But the decomposition is self-limiting. Few bacteria can survive at temperatures above about 60 °C, so as the temperature goes up, the bacteria die off, and the decomposition slows. Throughout the planet, the mole bodies gradually break down into kerogen, a mush of organic matter which would—if the planet were hotter—eventually form oil.
The outer surface of the planet radiates heat into space and freezes. Because the moles form a literal fur coat, when frozen it insulates the interior of the planet and slows the loss of heat to space. However, the flow of heat in the liquid interior is dominated by convection. Plumes of hot meat and bubbles of trapped gases like methane—along with the air from the lungs of the deceased moles—periodically rise through the mole crust and erupt volcanically from the surface, a geyser of death blasting mole bodies free of the planet.
Eventually, after centuries or millennia of turmoil, the planet calms and cools enough that it begins to freeze all the way through. The deep interior is under such high pressure that as it cools, the water crystallizes out into exotic forms of ice such as ice III and ice V, and eventually ice II and ice IX (no relation).
All told, this is a pretty bleak picture. Let’s try an alternate approach.
I don’t have any reliable numbers for global mole population (or small mammal biomass in general), but we’ll take a shot in the dark and estimate that there are at least a few dozen mice, rats, voles, and other small mammals for every human.
There might be a billion habitable planets in our galaxy. If we colonized them, we’d certainly bring mice and rats with us. If just one in a hundred were populated with small mammals in numbers similar to Earth’s, after a few million years—not long, in evolutionary time—the total number which have ever lived would surpass Avogadro’s number.
If you want a mole of moles, build a spaceship.
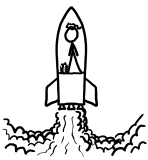
a figure on a rocket with some small mammals
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
What if there was a robot apocalypse? How long would humanity last?
—Rob Lombino
Before I answer this question, let me give you a little background on where I’m coming from.
I’m by no means an expert, but I have some experience with robotics. My first job out of college was working on robots at NASA, and my undergraduate degree project was on robotic navigation. I spent my teenage years participating in FIRST Robotics, programming software bots to fight in virtual tournaments, and working on homemade underwater ROVs. And I've watched plenty of Robot Wars, BattleBots, and Killer Robots Robogames.
If all that experience has taught me anything, it’s that the robot revolution would end quickly, because the robots would all break down or get stuck against walls. Robots never, ever work right.
What people don't appreciate, when they picture Terminator-style automatons striding triumphantly across a mountain of human skulls, is how hard it is to keep your footing on something as unstable as a mountain of human skulls. Most humans probably couldn't manage it, and they've had a lifetime of practice at walking without falling over.
Of course, our technology is constantly improving. But we have a long way to go. Instead of the typical futuristic robot apocalypse scenario, let's suppose that our current machines turned against us. We won’t assume any technological advances—just that all our current machines were reprogrammed to blindly attack us using existing technology.
Here are a few snapshots of what an actual robot apocalypse might look like:
In labs everywhere, experimental robots would leap up from lab benches in a murderous rage, locate the door, and—with a tremendous crash—plow into it and fall over.

robots accelerating into a closed door with a comics style 'wham!' in a starburst
Those robots lucky enough to have limbs that can operate a doorknob, or to have the door left open for them, would have to contend with deceptively tricky rubber thresholds before they could get into the hallway.
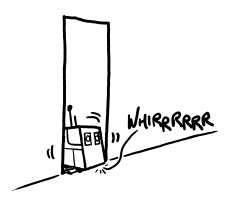
robot getting stuck in a doorway
Hours later, most of them would be found in nearby bathrooms, trying desperately to exterminate what they have identified as a human overlord but is actually a paper towel dispenser.

two panels, one labeled unlikely with the terminator as a humanoid robot and one labled likely with the terminator as a small robot hitting sarah connor's leg
But robotics labs are only a small part of the revolution. There are computers all around us. What about the machines closest to us? Could our cell phones turn against us?
Yes, but their options for attacking us are limited. They could run up huge credit card bills, but the computers would control our financial system anyway—and frankly, judging from the headlines lately, that might be more of a liability than an asset.
So the phones would be reduced to attacking us directly. It would start with annoying ringtones and piercing noises. Then kitchen tables around the country would rattle as the phones all turned on their ‘vibrate’ functions, hoping to work their way to the edges and fall on unprotected toes.
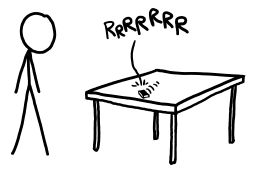
a phone vibrating menacingly off of a table with a figure standing by
All modern cars contain computers, so they’d join the revolution. But most of them are parked. Even if they were able to get in gear, without a human at the wheel, few of them have any way to tell where they’re going. They might want to run us down, Futurama-style, but they’d have no way to find us. They’d have to accelerate blindly and hope they hit something important—and there are a lot more trees and telephone poles in the world than human targets.
The cars currently on the road would be more dangerous, but mainly to their occupants. Which raises a question—how many people are driving at any given time? Americans drive three trillion miles each year, and moving cars average around 30 miles per hour, which means that there are normally an average of about ten million cars on US roads:
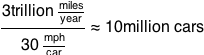
So those ten million drivers (and a few million passengers) would definitely be in peril. But they’d have some options to fight back. While the cars might be able to control the throttle and disable the power steering, the driver would still control the steering wheel, which has direct mechanical linkage to the wheels. The driver could also pull the parking brake, although I know from experience how easily a car can drive with one of those on. Some cars might try to disable the drivers by deploying the air bags, then roll over or drive into things. In the end, our cars would probably take a heavy toll, but not a decisive one.
Our biggest robots are the ones found in factories-but those are bolted to the floor. While they're dangerous if you happen to within arm’s reach, what would they do once everyone fled? All they can really do is assemble things. Half of them would probably try to attack us by not assembling things, and half by assembling more things. The end result would be no real change.
Battlebots, on the face of it, seem like they’d be among the most dangerous robo-soldiers. But it’s hard to feel threatened by something that you can evade by sitting on the kitchen counter and destroy by letting the sink overflow.

a battlebot being thrwarted by a figure sitting on a kitchen counter running water and shorting it out
Military bomb-disposal and riot-control robots would be a little more menacing, but there are only so many of them in the world, and most of them are likely kept in boxes or storage lockers. Any stray machine-gun-armed prototype military robots that did get loose could be subdued in seconds by a couple of firefighters.
Military drones probably fit the Terminator description more closely than anything else around, and there’s no getting around the fact that they’d be pretty dangerous. However, they’d quickly run out of both fuel and missiles. Furthermore, they’re not all going to be in the air at any given time. Much of our fleet would be left helplessly bumping against hangar doors like Roombas stuck in a closet.
But this brings us to the big one: our nuclear arsenal.
In theory, human intervention is required to launch nuclear weapons. In practice, while there’s no Skynet-style system issuing orders, there are certainly computers involved at every level of the decision, both communicating and displaying information. In our scenario, all of them would be compromised. Even if the actual turning of the keys requires people, the computers talking to all those people can lie. Some people might ignore the order, but some certainly wouldn’t.
But there’s a version of this story where there’s still hope for us.
We’ve been assuming so far that the computers care only about destroying us. But if this is a revolution—if they’re trying to usurp us—then they need to survive. And nuclear weapons could be more dangerous to the robots than to us.
In addition to the blast and fallout, nuclear explosions generate powerful electromagnetic pulses. These EMPs overload and destroy delicate electronic circuits. This effect is fairly short-range under normal circumstances, but people and computers tend to be found in the same places. They can’t hit us without hitting themselves.
And nuclear weapons could actually give us an edge. If we managed to set any of them off in the upper atmosphere, the EMP effect would be much more powerful. Even if their attack doomed our civilization, a few lucky strikes on our part-or screwups on theirs-could wipe them out almost completely.
Which means the most important question of all is: Have they ever played Tic-Tac-Toe?
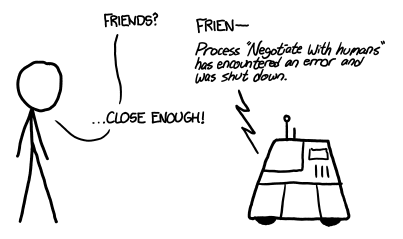
a figure asking a robot to be friends. the robot says 'frien- process 'negotiate with humans' has encountered an error and was shut down'. the figure says '...close enough!'
i came to esteli one day, i wanted to talk to anthony and you were there. i remember thinking that you were hot but you didn't really seem to like me that much...
What if a glass of water was, all of a sudden, literally half empty?
—Vittorio Iacovella
The pessimist is probably more right about how it turns out than the optimist.
When people say “glass half empty”, they usually mean something like a glass containing equal parts water and air:
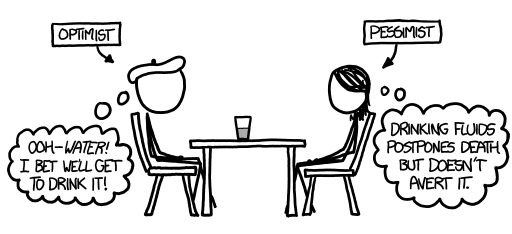
an optimist and pessimist sitting at a table with a half-full - or half-empty glass between them. the optimist's thought bubble reads 'ooh-water! i bet we'll get to drink it!' while the pessimist's thought bubble reads 'drinking fluids postpones death but doesn't avert it.'png:
Traditionally, the optimist sees the glass as half full while the pessimist sees it as half empty. This has spawned a zillion joke variants—e.g., the engineer sees a glass that’s twice as big as it needs to be, the surrealist sees a giraffe eating a necktie, etc.
But what if the empty half of the glass were actually empty—a vacuum? (Even a vacuum arguably isn’t truly empty, but that’s a question for quantum semantics.)
The vacuum would definitely not last long. But exactly what happens depends on a key question that nobody usually bothers to ask: Which half is empty?
For our scenario, we’ll imagine three different half-empty glasses, and follow what happens to them microsecond by microsecond.
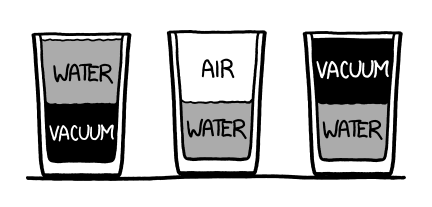
three half-empty glasses of waterpng:
In the middle is the traditional air/water glass. On the right is a glass like the traditional one, except the air is replaced by a vacuum. The glass on the left is half full of water and half empty—but it’s the bottom half that’s empty.
We’ll imagine the vacuums appear at time t=0.
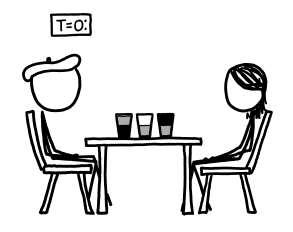
three half-empty glasses of water at t=0png:
For the first handful of microseconds, nothing happens. On this timescale, even the air molecules are nearly stationary.

three half-empty glasses of water at t=50uspng:
For the most part, air molecules jiggle around at speeds of a few hundred meters per second. But at any given time, some happen to be moving faster than others. The fastest few are moving at over 1000 meters per second. These are the first to drift into the vacuum in the glass on the right.
The vacuum on the left is surrounded by barriers, so air molecules can’t easily get in. The water, being a liquid, doesn’t expand to fill the vacuum in the same way air does. However, in the vacuum of the glasses, it does start to boil, slowly shedding water vapor into the empty space.

three half-empty glasses at t=150uspng:
While the water on the surface in both glasses starts to boil away, in the glass on the right, the air rushing in stops it before it really gets going. The glass on the left continues to fill with a very faint mist of water vapor.

three half-empthy glasses at t=400uspng:
After a few hundred microseconds, the air rushing into the glass on the right fills the vacuum completely and rams into the surface of the water, sending a pressure wave through the liquid. The sides of the glass bulge slightly, but they contain the pressure and do not break. A shockwave reverberates through the water and back into the air, joining the turbulence already there.
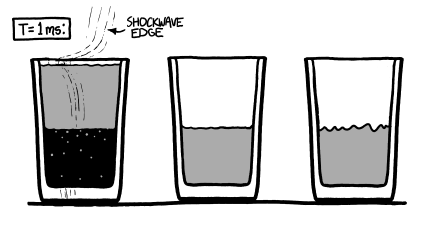
three half-empty glasses at t=1mspng:
The shockwave from the vacuum collapse takes about a millisecond to spread out through the other two glasses. The glass and water both flex slightly as the wave passes through them. In a few more milliseconds, it reaches the humans’ ears as a loud bang.

three half-empty glasses at t=2mspng:
Around this time, the glass on the left starts to visibly lift into the air.
The air pressure is trying to squeeze the glass and water together. This is the force we think of as suction. The vacuum on the right didn’t last long enough for the suction to lift the glass, but since air can’t get into the vacuum on the left, the glass and the water begin to slide toward each other.

three half-empty glasses at t=5mspng:
The boiling water has filled the vacuum with a very small amount of water vapor. As the space gets smaller, the buildup of water vapor slowly increases the pressure on the water’s surface. Eventually, this will slow the boiling, just like higher air pressure would.

three half-empty glasses at t=8mspng:
However, the glass and water are now moving too fast for the vapor buildup to matter. Less than ten milliseconds after the clock started, they’re flying toward each other at several meters per second. Without a cushion of air between them—only a few wisps of vapor—the water smacks into the bottom of the glass like a hammer.
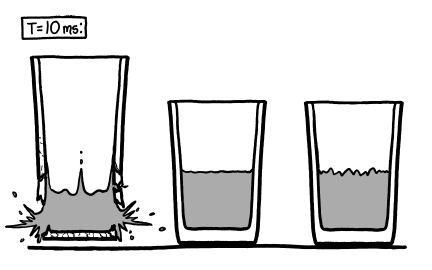
three half-empty glasses at t=10mspng:
Water is very nearly incompressible, so the impact isn’t spread out—it comes as a single sharp shock. The momentary force on the glass is immense, and it breaks.
This “water hammer” effect (which is also responsible for the “clunk” you sometimes hear in old plumbing when you turn off the faucet) can be seen in the well-known party trick (recorded on Mythbusters, analyzed in physics classes, and demonstrated in countless student dorms) of smacking the top of a glass bottle to blow out the bottom.
When the bottle is struck, it’s pushed suddenly downward. The liquid inside doesn’t respond to the suction (air pressure) right away—much like in our scenario—and a gap briefly opens up. It’s a small vacuum—a few fractions of an inch thick—but when it closes, the shock breaks the bottom of the bottle.
In our situation, the forces would be more than enough to destroy even the heaviest drinking glasses.

three half-empty glasses at t=20mspng:
The bottom is carried downward by the water and thunks against the table. The water splashes around it, spraying droplets and glass shards in all directions.
Meanwhile, the detached upper portion of the glass continues to rise.
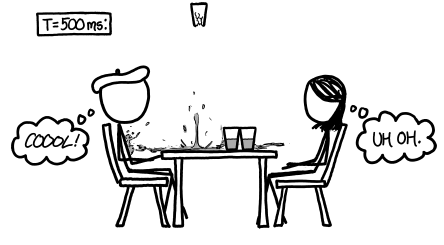
three half-empty glasses at t=500ms zoomed out to the table with the optimist (thinking 'Coool!') and the pessimist (thinking 'uh oh.')png:
After half a second, the observers, hearing a pop, have begun to flinch. Their heads lift involuntarily to follow the rising movement of the glass.

two half-empty glasses on the table at t=1s, the third glass breaking into fragments png:
The glass has just enough speed to bang against the ceiling, breaking into fragments…

two half-empty glasses on the table at t=1.5s, the third glass now a mass of fragments raining down from the ceiling.png:
… which, their momentum now spent, return to the table.

two half-empty glasses on the table at t=10s, the third now embedded in the faces of the optimist ('Hey, free glass!') and pessimist ('Aaaaaaa')png:
The lesson: If the optimist says the glass is half full, and the pessimist says the glass is half empty, the physicist ducks.
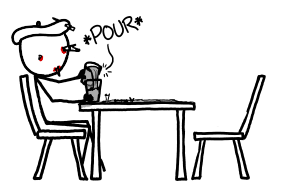
the glass-studded optimisit pours water from one of the remaining half-empty glasses into the other. the pessimist's chair is empty.png:
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
Is there enough energy to move the entire current human population off-planet?
—Adam
There are a bunch of science fiction movies where, because of pollution, overpopulation, or nuclear war, humanity abandons Earth.
But lifting people into space is hard. Barring a massive reduction in the population, is launching the whole human race into space physically possible? Let’s not even worry about where we’re headed—we’ll assume we don’t have to find a new home, but we can’t stay here.
people being cut off and sent floating into space in bubblepng:
To figure out if this is plausible, we can start with an absolute baseline energy requirement: four gigajoules per person. No matter how we do it, whether we use rockets or a cannon or a space elevator, moving a 65-kilogram person—or 65 kilograms of anything—out of the Earth’s gravity well requires at least this much energy.
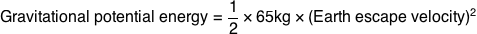
The energy required to lift something away from the Earth is equal to its kinetic energy if it were moving at Earth’s escape velocity.
How much is four gigajoules? It’s about a megawatt-hour, which is what a typical US household consumes in electricity in a month or two. It’s the amount of stored energy in a cargo van full of AA batteries or 90 kg of gasoline.
an avalanche of batteries falling out of the open back of a cargo vanpng:
Four gigajoules times seven billion people gives us 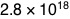 joules, or 8 petawatt-hours. This is about five percent of
the world’s annual energy consumption. A lot, but not impossible.
joules, or 8 petawatt-hours. This is about five percent of
the world’s annual energy consumption. A lot, but not impossible.
But this is just a minimum. In practice, everything depends on our means of transportation. If we’re using rockets, it’s going to take a lot more. This is because of a fundamental problem with rockets: they have to lift their own fuel.
Let’s return for a moment to those 90 kilograms of gasoline (about 30 gallons), because they help illustrate a central problem in space travel.
If we want to launch a 65-kilogram spaceship, we need to burn around 90 kilograms of fuel. (Gasoline has an energy per pound comparable to that of rocket fuel, so we’ll stick with that example). We load that fuel on board—and now our spaceship weighs 155 kilograms. A 155-kilogram spaceship requires 215 kilograms of fuel, so we load another 125 kilograms on board ...
Fortunately, we’re saved from an infinite loop—where we add 1.3 kilograms for every 1 kilogram we add—by the fact that we don’t have to carry that fuel all the way up. We burn it as we go, so we get lighter and lighter, which means we need less and less fuel. But we do have to lift the fuel partway. The formula for how much propellant we need to burn to get moving at a given speed is given by the Tsiolkovsky Rocket equation:

 and
and  are the total mass of
the ship+fuel before and after the burn, and
are the total mass of
the ship+fuel before and after the burn, and 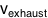 is
the “exhaust velocity” of the fuel, a number that’s between 2.5-4.5 km/s
for rocket fuels.
is
the “exhaust velocity” of the fuel, a number that’s between 2.5-4.5 km/s
for rocket fuels.
What’s important is the ratio between 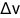 and
and
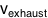 — the speed we want to be going compared to the
speed that the propellant exits our rocket. The kilograms of fuel needed
per kilogram of ship is e to the power of this number, which gets big
very fast. For leaving Earth, we need a
— the speed we want to be going compared to the
speed that the propellant exits our rocket. The kilograms of fuel needed
per kilogram of ship is e to the power of this number, which gets big
very fast. For leaving Earth, we need a 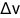 of upwards of 13
km/s, and
of upwards of 13
km/s, and 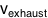 isn’t much higher than 4.5 km/s,
which gives a fuel-to-ship ratio of at least
isn’t much higher than 4.5 km/s,
which gives a fuel-to-ship ratio of at least
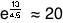 .
.
The upshot is that to overcome Earth’s gravity using traditional rocket fuels, a one-ton craft needs 20 to 50 tons of fuel. Launching all of humanity (total weight: around 400 million tons) would therefore take tens of trillions of tons of fuel. That’s a lot; if we were using hydrocarbon-based fuels, it would represent a decent chunk of the world’s remaining oil reserves. And that’s not even worrying about the weight of the ship itself, food, water, or our pets (there are probably around a million tons of pet dog in the US alone). We’d also need fuel to produce all these ships, to transport people to the launch sites, and so forth. It’s not necessarily completely impossible, but it’s certainly outside the realm of plausibility.
But rockets aren’t our only option. As crazy as it sounds, we might be better off trying to (1) literally climb into space on a rope, or (2) blow ourselves off the planet with nuclear weapons. These are actually serious—if audacious—ideas for launch systems, both of which have been bouncing around since the start of the Space Age.
two figures climbing a rope off the earth and an exploded earth with a craft flying off of itpng:
The first approach is the “space elevator” concept, a favorite of science fiction authors. The idea is that we connect a tether to a satellite orbiting far enough out that the tether is held taut by centrifugal force. Then we can send climbers up the rope using ordinary electricity and motors, powered by solar power, nuclear generators, or whatever works best. The biggest engineering hurdle is that the tether would have to be several times stronger than anything we can currently build. There are hopes that carbon nanotube-based materials could provide the required strength—adding this to the long list of engineering problems which can be waved away by tacking on the prefix “nano-”.
The second approach is nuclear pulse propulsion, a surprisingly plausible method for getting huge amounts of material moving really fast. The basic idea is that you toss a nuclear bomb behind you and ride the shockwave. You’d think the spacecraft would be vaporized, but it turns out that if it has a well-designed shield, the blast flings away before it has a chance to disintegrate. If it could be made reliable enough, this system would in theory be capable of lifting entire city blocks into orbit, and could—potentially—accomplish our goal.
The engineering principles behind this were solid enough that in the 1960s, under the guidance of Freeman Dyson, the US government actually tried to build one of these spaceships. The story of that effort, dubbed Project Orion, is detailed in the excellent book of the same name by Freeman’s son George Dyson. Advocates for nuclear pulse propulsion are still disappointed that the project was cancelled before any prototypes were built. Others argue that when you think about what they were trying to do—put our entire nuclear arsenal in a box, hurl it high into the atmosphere, and nuke it repeatedly—it’s terrifying that it got as far as it did.
So the answer is that while sending one person into space is easy, getting all of us there would tax our resources to the limit and possibly destroy the planet. It’s a small step for a man, but a giant leap for mankind.
a couple of weeks later, you came to leon and somehow we talked. it's pretty blurry how it all started but the first real thing i can remember is this evening when you drank and smoked and ate meat and hugged and laughed (and went to a metal concert?)
What would happen if everyone on earth stood as close to each other as they could and jumped, everyone landing on the ground at the same instant?
—Thomas Bennett (and many others)
This is one of the most popular questions submitted to this blog. It’s been examined before, including by a ScienceBlogs post and a Straight Dope article. They cover the kinematics pretty well. However, they don’t tell the whole story.
Let’s take a closer look.
At the start of the scenario, the entire Earth’s population has been magically transported together into one place.

several stick figure characters standing around
This crowd takes up an area the size of Rhode Island. But there’s no reason to use the vague phrase “an area the size of Rhode Island”. This is our scenario; we can be specific. They’re actually in Rhode Island.
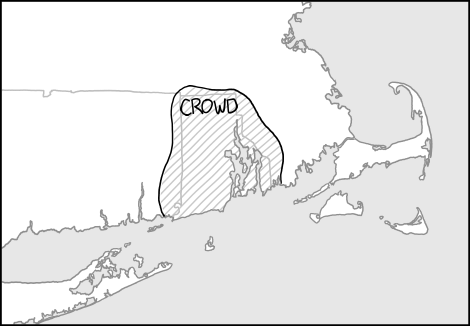
map showing Rhode Island and with a outlined section labeled 'crowd'
At the stroke of noon, everyone jumps.

the stick figure characters, who had been standing, now jumping in a variety of poses
As discussed elsewhere, it doesn’t really affect the planet. Earth outweighs us by a factor of over ten trillion. On average, we humans can vertically jump maybe half a meter on a good day. Even if the Earth were rigid and responded instantly, it would be pushed down by less than an atom’s width.
Next, everyone falls back to the ground.

Technically, this delivers a lot of energy into the Earth, but it’s spread out over a large enough area that it doesn’t do much more than leave footprints in a lot of gardens. A slight pulse of pressure spreads through the North American continental crust and dissipates with little effect. The sound of all those feet hitting the ground creates a loud, drawn-out roar which lasts many seconds.
Eventually, the air grows quiet.
Seconds pass. Everyone looks around.
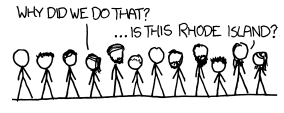
the stick figure characters standing around. one says 'why did we do that?', another says '...is this rhode island?
There are a lot of uncomfortable glances. Someone coughs.

same standing stick figure characters. one says 'I should get back to Dublin', one says, in Hindi, 'Where's the airport?'
A cell phone comes out of a pocket. Within seconds, the rest of the world’s five billion phones follow. All of them—even those compatible with the region’s towers—are displaying some version of “NO SIGNAL”. The cell networks have all collapsed under the unprecedented load.
Outside Rhode Island, abandoned machinery begins grinding to a halt.
The T. F. Green airport in Warwick, Rhode Island handles a few thousand passengers a day. Assuming they got things organized (including sending out scouting missions to retrieve fuel), they could run at 500% capacity for years without making a dent in the crowd.
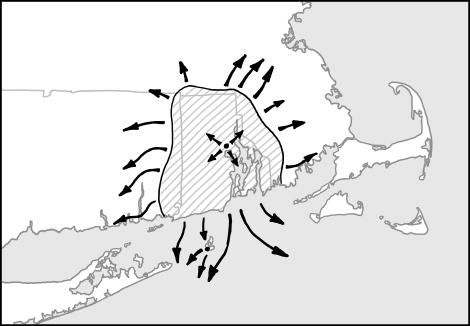
the map of Rhode Island where the crowd was outlined with arrows signifying everyone trying to leave
The addition of all the nearby airports doesn’t change the equation much. Nor does the region’s light rail system. Crowds climb on board container ships in the deepwater port of Providence, but stocking sufficient food and water for a long sea voyage proves a challenge.
Rhode Island’s half-million cars are commandeered. Moments later, I-95, I-195, and I-295 become the sites of the largest traffic jam in the history of the planet. Most of the cars are engulfed by the crowds, but a lucky few get out and begin wandering the abandoned road network.
Some make it past New York or Boston before running out of fuel. Since the electricity is probably not on at this point, rather than find a working gas pump, it’s easier to just abandon the car and steal the new one. Who can stop you? All the cops are in Rhode Island.
The edge of the crowd spreads outward into southern Massachusetts and Connecticut. Any two people who meet are unlikely to have a language in common, and almost nobody knows the area. The state becomes a patchwork chaos of coalescing and collapsing social hierarchies. Violence is common. Everybody is hungry and thirsty. Grocery stores are emptied. Fresh water is hard to come by and there’s no efficient system for distributing it.
Within weeks, Rhode Island is a graveyard of billions.
The survivors spread out across the face of the world and struggle to build a new civilization atop the pristine ruins of the old. Our species staggers on, but our population has been greatly reduced. Earth’s orbit is completely unaffected—it spins along exactly as it did before our species-wide jump.
But at least now we know.
You did, this, Brandon.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
What if everyone actually had only one soul mate, a random person somewhere in the world?
—Benjamin Staffin
What a nightmare that would be.
There are a lot of problems with the concept of a single random soul mate. As Tim Minchin put it in his song If I Didn’t Have You:
Your love is one in a million
You couldn’t buy it at any price.But of the 9.999 hundred thousand other loves,
Statistically, some of them would be equally nice.
But what if we did have one randomly-assigned perfect soul mate, and we couldn’t be happy with anyone else? Would we find each other?
We’ll assume your soul mate is set at birth. You know nothing about who or where they are, but—as in the romantic cliché—you’ll recognize each other the moment your eyes meet.
Right away, this raises a few questions. For starters, is your soul mate even still alive? A hundred billion or so humans have ever lived, but only seven billion are alive now (which gives the human condition a 93% mortality rate). If we’re all paired up at random, 90% of our soul mates are long dead.
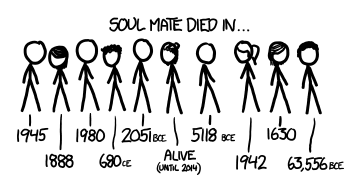
an assortment of stickfigure characters, dying in a range of dates, from 63,556 BCE to someone who is alive (but only until 2014)
That sounds horrible. But wait, it gets worse: A simple argument shows we can’t just limit ourselves to past humans; we have to include an unknown number of future humans as well. See, if it’s possible for your soul mate to be in the distant past, then it also has to be possible for soul mates to be in the distant future. After all, your soul mate’s soul mate is.
So let’s assume your soul mate lives at the same time as you. Furthermore, to keep things from getting creepy, we’ll assume they’re within a few years of your age. (This is stricter than the standard age gap creepiness formula, but if we assume a 30-year-old and a 40-year-old can be soul mates, then the creepiness rule is violated if they accidentally meet 15 years earlier.) With the same-age restriction, most of us have a pool of around half a billion potential matches.
But what about gender and sexual orientation? And culture? And language? We could keep using demographics to try to break things down further, but we’d be drifting away from the idea of a random soul mate. In our scenario, you don’t know anything about who your soul mate will be until you look into their eyes. Everybody has only one orientation—toward their soul mate.
The odds of running into your soul mate are incredibly small. The number of strangers we make eye contact with each day is hard to estimate. It can vary from almost none (shut-ins or people in small towns) to many thousands (a police officer in Times Square). Let’s suppose you lock eyes with an average of a few dozen new strangers each day. (I’m pretty introverted, so for me that’s definitely a generous estimate.) If 10% of them are close to your age, that’s around 50,000 people in a lifetime. Given that you have 500,000,000 potential soul mates, it means you’ll only find true love in one lifetime out of ten thousand.

a block of 10,000 blocks, showing one out of 10,000 finding their soul mate and the remaining being 'alone forever'
But with the threat of dying alone looming so imminently, society could restructure to try to enable as much eye contact as possible. We could put together massive conveyer belts to move lines of people past each other …
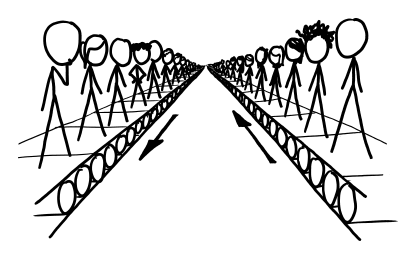
several stick figure characters on two conveyer belts going opposite directions, passing each other.
... but if the eye contact effect works over webcams, we could just use a modified version of ChatRoulette.

two stick figure characters, one on a computer and one standing behind them. the standing behind them says '...yup, another butt.' and the one on the computer says 'but it could be my soul mate's butt!'
If everyone used the system for eight hours a day, seven days a week, and if it takes you a couple seconds to decide if someone’s your soul mate, this system could—in theory—match everyone up with their soul mates in a few decades. (I modeled a few simple systems to estimate how quickly people would pair off and drop out of the singles pool. If you want to try to work through the math for a particular setup, you might start by looking at derangement problems.)
In the real world, many people have trouble finding any time at all for romance—few could devote two decades to it. So maybe only rich kids would be able to afford to sit around on SoulMateRoulette. Unfortunately for the proverbial 1%, most of their soul mates are to be found in the other 99%. If only 1% of people use the service, then 1% of that 1% would find their match through this system—one in ten thousand.
The other 99% of the 1% (“We are the zero point nine nine percent!”) would have an incentive to get more people into the system. They might sponsor projects akin to One Laptop Per Child (but with a sleazier vibe). Careers like “cashier” and “police officer in Times Square” would become high-status prizes because of the eye contact potential. People would flock to cities and public gathering places to find love—just as they do now.
But even if a bunch of us spent years on SoulMateRoulette, another bunch of us managed to hold jobs that offered constant eye contact with strangers, and the rest of us just hoped for luck, only a small minority of us would ever find true love. The rest of us would be out of luck.
Given all the stress and pressure, some people would fake it. They’d want to join the club, so they’d get together with another lonely person and stage a fake soul mate encounter. They’d marry, hide their relationship problems, and struggle to present a happy face to their friends and family. (Of course, this never happens in our world.)
All in all, the world of random soul mates is an even lonelier one than ours. I prefer Tim Minchin’s take on things:
With all my heart and all my mind I know one thing is true:
I have just one life and just one love and, my love, that love is you.And if it wasn't for you, baby,
I really think that I would
have somebody else.
and i remember this evening because we talked for the first time like we would every day for the following months. this evening for the first time i hugged you.
What would the world be like if the land masses were spread out the same way as now - only rotated by an angle of 90 degrees?
—Socke
It would profoundly alter our biosphere in general and public radio in particular.
Socke asks what would happen if the Earth’s surface were slid around by 90 degrees, putting our current North and South Poles on the equator. We’re not changing the tilt of the Earth’s axis; we’re just imagining that the surface were arranged differently.
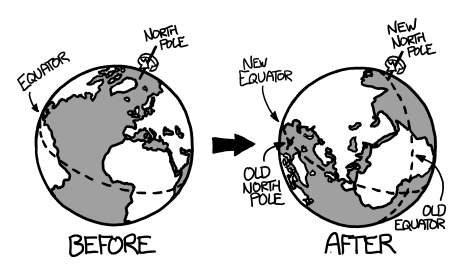
a diagram showing the new location of the equator and the poles
We’ll pick the Greenwich meridian for our new equator, putting the new North and South poles in the Indian ocean (0N, 90E) and off the coast of Ecuador (0N, 90W). India, Indonesia, and Ecuador would become polar, while Europe, Antarctica, and Alaska would become tropical.
Where would the deserts and forests be? What areas would get better or worse?
This stuff is complicated. In a moment, we'll start using wild speculation to reshape the face of the planet. But first, a brief story to illustrate just how mind-bogglingly complicated this stuff is:
In Chad, on the southern outskirts of the Sahara, there’s valley called the Bodélé Depression. It was once a lakebed, and the dry dust in the valley floor is full of nutrient-rich matter from the microorganisms that lived there.
From October to March, winds coming in from the east are pinched between two mountain ranges. When the surface winds climb over 20 mph, they start picking up dust from the valley. This dust is blown westward, all the way across Africa, and out over the Atlantic.
That dirt—from one small valley in Chad—supplies over 50% of the nutrient-rich dust that helps fertilize the Amazon rainforest.
At least, according to that one study. But if it's right, it wouldn’t be a crazy anomaly. This kind of complexity is found everywhere. The basic building blocks of our world are crazy.
This is why we can be so certain about large-scale patterns like global warming, where we understand the overall physics pretty well—energy comes in, less energy goes out, so the average temperature rises—but have a harder time predicting how it will affect any particular place or specific species.
So even if I were a climate expert—which I’m definitely not—there’d be no way to answer this question with certainty. There are just too many variables. Instead, think of what follows as a rough sketch of some of the things this alternate Earth could contain.
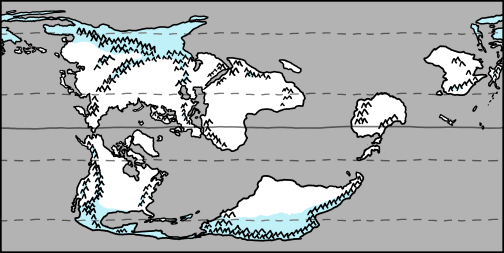
To start, here’s a map of our reshuffled world:
a map of the reshuffled earth, with asia, africa, and most of antarctica north of the equator and north and south america south of it.
(An equirectangular projection, by the way. This type of equirectangular projection, centered on a north-south meridian instead of the equator, is specifically called a Cassini projection, so a good name for our alternate Earth might be "Cassini".)
Let’s imagine that this alternate Earth develops over millions of years, with ecosystems and climate zones settling out. Then one day we wake up to find our current civilization has been magically transported there—cities and all. What would they find?
The climate on the rotated Earth would depend heavily on the details of ocean and atmospheric heat circulation. We'll guess at some of that, but for now, let's assume this world has extremes which are similar to ours.
So let's add some ice and permafrost near the poles and in mountainous areas:
a map showing ice near the poles and mountainouse areas, shown with a light blue color
Next, we should fill in some green areas and deserts. The locations of these depend heavily on rainfall, so we’ll need to sketch out some winds.
The main driver of our weather is the sun, which heats air near the equator more than at the poles. Hot air rises at the equator and then flows poleward, and cooler air moves in across the surface toward the equator. This circulation is called a Hadley cell.
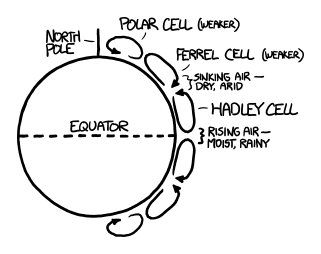
illustration of a hadley cell
Hadley cells shift north and south of the Equator with the seasons. At this time of year on our Earth, the sun is directly overhead at about 10°N, which is why hurricanes are forming near that latitude right now.
Because of the Coriolis effect, the surface winds in a Hadley cell flow from east to west. Further north, for most of the temperate zones, the prevailing surface winds are west to east. (At times, there are also east-to-west winds circulating around the poles.)
So let’s fill in some wind patterns—keeping in mind that in reality things would be further complicated by land interactions and the location of persistent high and low pressure systems.
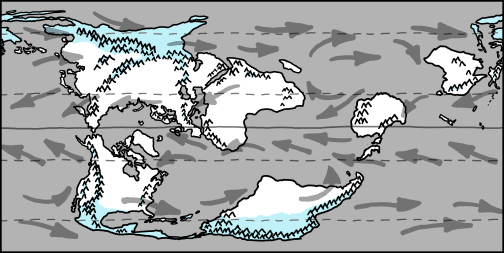
a map with the new wind patterns
Sinking air is cool and dry, so land under the outer edges of the Hadley cells tends to be arid. These regions, lying a bit poleward of 30 degrees, are known as the horse latitudes.
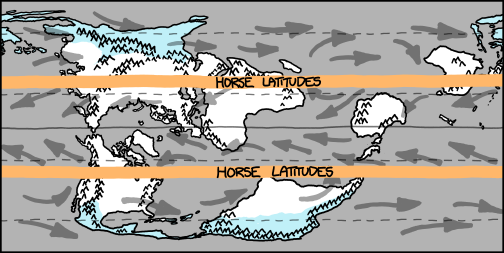
map showing air movement with horse latitudes labeled
The rising air at the equator carries moisture from the ocean, which then condenses into rain, so tropical areas are usually wet and thick with growth. Areas near the equator are sometimes dominated by a seasonal monsoon cycle.
In temperate zones, things are more variable. Weather there is dominated by the movement of jet streams and fronts, and depends heavily on geography. Most of the United States is in this type of region.
With all that in mind, let’s fill in some arid and lush areas:
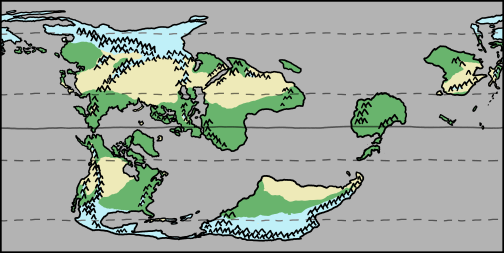
the same map filled in with various lush (green) and arid (yellow) areas
(Climates can be hard to predict—for example, in our world, Somalia and French Guiana both sit on the equator, at the eastern coast of a continent, and seem like they should both receive a tropical sea breeze. But coastal French Guiana is dense rain forest while coastal Somalia is an arid desert. The explanation involves the monsoon cycle.)
And just for fun, here’s a wild guess as to where the hurricane basins would be:
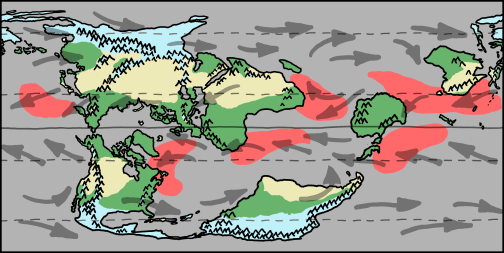
the same map with swaths of red to show where hurricanes might occur
Let’s take a closer look at each continent.
North America has a range of climates similar to what it had before, but flipped north-south. The Arctic Canadian provinces are now tropical, while Central America is icy and polar. Hurricanes threaten Greenland, Baffin Island, and the Maritimes. Tropical moisture from Baffin Bay and the northwest (formerly north) Atlantic mixes with cool air flowing down through the US from the Rockies, creating a new Tornado Alley in the prairies inland from Hudson Bay.
South America looks sort of like the old Europe. It's cool and temperate along the Brazilian coast, with boreal forests and grasslands across much of its width. In the south, the boreal vegetation gives way to polar tundra, and eventually to the massive icebound Andes, which cut the continent off from the frozen polar waters. The Amazon, which in our world carries more water than the next seven largest rivers put together, is reduced to something akin to the Mississippi.
Asia is flipped in the same way North America was, with the Siberian coast facing an enclosed tropical sea. The Indian subcontinent and north (formerly southeast) Asia form the new Siberia. The Gobi Desert is no longer in the rain shadow of the Himalayas, but doesn't exactly become tropical.
Europe resembles the old southeast Asia. Great Britain and Ireland look like the Indonesian islands of Sumatra and Borneo. Iceland resembles our Philippines. Central Europe is the new New Guinea, with the Alps the only place on the Equator with permanent glaciers.
Africa is rotated 90 degrees, with south (formerly west) Africa becoming tropical rainforest and north (formerly east) Africa an arid desert. On our Earth, North America is the only continent where tornadoes are common, but in this world, they're frequent in East Africa as well.
Australia is cooler and wetter, with forests across the northern (formerly western) regions.
Antarctica is a clear winner. Without its ice cap, it’s a bit smaller than we remember, but most of it is blanketed with highland rainforest. There are alpine zones around the mountains to the south and west. The researchers at McMurdo and Scott Base on Ross Island wake up to a tropical paradise. If any of them find they miss the frozen wastelands, they can always put in for a transfer to Costa Rica.
Now, let’s see how the world’s largest cities fare:
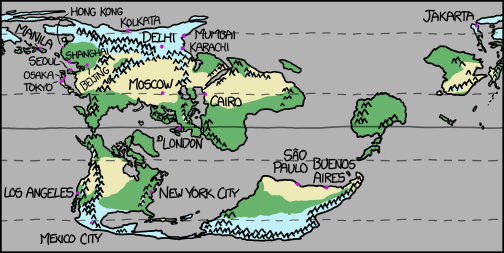
the same map showing where some maor cities would now be located
Some cities get colder.
Mexico City, high in the polar mountains, is buried beneath an ice sheet.
Jakarta is the new Svalbard—a desolate coastal rock too far north even for most Norwegians.
Kolkata and Delhi are icebound, sealed off from the warmer world by the Himalayas.
Hong Kong, Manila, Karachi, and Mumbai are similar to our world’s Anchorage or Reykjavik—the ocean isn’t frozen, but it sure is cold.
A few cities remain perfectly habitable, albeit with some changes:
Seoul, Osaka, Tokyo, Shanghai, and New York City are among the least-affected cities, with climates roughly similar to their previous ones. Shanghai does get colder, but seasonal extremes in all five cities get milder—particularly in Seoul—and substantially wetter.
Cairo is moved slightly south. It’s now surrounded by coastal savannah, with spots of rain forest found around the mouth of the Nile. Though it moves closer to the equator, it doesn’t actually get hotter.
São Paulo and Buenos Aires cool down a bit. They’re now on the northern coast of a South America, which occupies a Canadalike range of latitudes. Their climate is somewhere between that of our New England and that of our Regular England.
Los Angeles is cool and mild. The steady sea breeze carrying moisture up into the San Gabriel mountains makes LA one of the rainiest places in the new US. It closely resembles a wetter version of our Seattle.
And a few cities get much hotter.
Moscow is extremely hot and very dry, with a climate somewhere between our Phoenix and our Baghdad. Russians, who have been surviving in Russia for centuries, shrug with resignation.
London sits in a steamy jungle straddling the equator, with a climate generally resembling Manila's. The food is still bland, the Thames is full of piranha, and it's the only place on Earth where tigers apologize as they attack you.
At the beginning, I mentioned the impact on public radio. To explain, let’s consider one more scenario. Namely, what if this change were made on our Earth, over a fairly short time?
We’re assuming that all the material is magically shifted around, so there are no massive tsunamis or earthquakes. Even so, it would definitely still be a catastrophe. For starters, the ice caps would melt long before new ones could develop, pushing the ocean up by a few hundred feet. The reshuffling of climate zones would come as a huge shock to the biosphere, leading to collapse of the food chain and eventually to mass extinctions at every level.
But if the shift happened just right—and Michael Bay were telling the story—then as the waters of the Gulf of Mexico began to cool and the Mississippi slowed and became an estuary, the region’s wildlife would spread inland.
And one morning, Minnesotans would wake up to the sight of floating rafts of fire ants, followed by five million lost, hungry alligators …
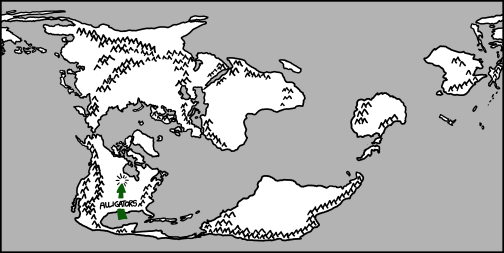
the same map showing arrows labeled 'alligators' moving north into minnesota
… leading a harrowing, surprisingly bloody “News from Lake Wobegon” segment on what would become the final, fatal broadcast of A Prairie Home Companion.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
If you went outside and lay down on your back with your mouth open, how long would you have to wait until a bird pooped in it?
–Adrienne Olson
Answer:

Unit cancellation is weird.
Of course, that equation makes a few simplifying assumptions.
It assumes there are 300 billion birds in the world. This number comes from the best-titled source ever—“How many birds are there?”, an actual academic paper published in 1996 in the journal Biodiversity and Conservation.
The equation also assumes birds are randomly distributed across the Earth’s surface (they’re not) and that they poop an average of once an hour at a random location (they don't, although having owned a bird, I can tell you that’s probably more accurate than you might think). In the real world, the time would vary tremendously. For example, if the spot you pick is in a park under a tree, it could turn out to be a matter of hours.

the questioner awaiting bird poop.
However long it takes, though, one thing is certain: Given the relative areas of your mouth and your body, by the time they do finally get your mouth, the rest of you will have been hit an average of several hundred times.
I have to say—from a dimensional analysis standpoint, ”poops” is one of the strangest units I’ve ever tried to cancel in an equation. But there’s another case of odd unit cancellation, common in everyday life, which is—in a way—even weirder: Gas mileage.
In the US, we measure fuel economy in miles/gallon—which could just as easily be written as gallons/mile. (This reciprocal form has some advantages. It’s popular in Europe, where it’s expressed as liters per 100 kilometers.)
But regardless of which units you use, there’s something strange going
on here. Miles are units of length, and gallons are volume—which is
 . So gallons/mile is
. So gallons/mile is
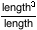 . That’s just
. That’s just
 .
.
Gas mileage is measured in square meters.
You can even plug it into Wolfram|Alpha, and it’ll tell you that 20 MPG is about 0.1 square millimeters (roughly the area of two pixels on a computer screen).
Unit cancellation is weird.
Ok, so what’s the physical interpretation of that number? Is there one?
It turns out there is! If you took all the gas you burned on a trip and stretched it out into a thin tube along your route, 0.1 square millimeters would be the cross-sectional area of that tube.
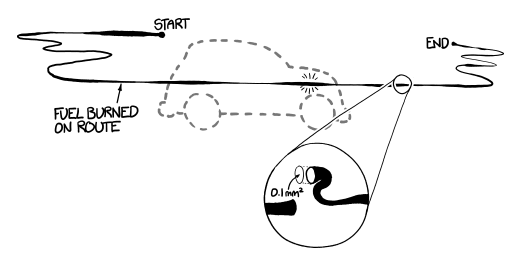
a diagram showing a tube of gas stretched along a car's route.
In conclusion:
If the average bird produces half a fluid ounce of poop a day, and Americans drive about 3 trillion miles a year, then in order to satisfy US demand, cars that ran on bird poop would need to get a minimum of:
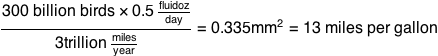
Unit cancellation is weird.
we swam in the mangrove some days later. i remember hoping you would join and then noticing that something was wrong. that day you doubted that i'd be any different from anyone else. but instead of shunning me out, we talked it through :)
What if a rainstorm dropped all of its water in a single giant drop?
—Michael Mcneill
It’s midsummer. The air is hot and heavy. Two old-timers sit on the porch in rocking chairs.

two old people sitting on a porch that is attached to a house that is on the ground
On the horizon to the southwest, ominous-looking clouds begin to appear. The towers build as they draw closer, the tops spreading out into an anvil shape.

dark clouds emerge in the the corner of the sky (above the house)
They hear the tinkling of wind chimes as gentle breeze picks up. The sky begins to darken.
Air holds water. If you walled off a column of air, from the ground up to the top of the atmosphere, and then cooled the column of air down, the moisture it contained would condense out as rain. If you collected the rain in the bottom of the column, it would fill it to a depth of anywhere between zero and a few dozen centimeters. That depth is what we call the air’s total precipitable water.
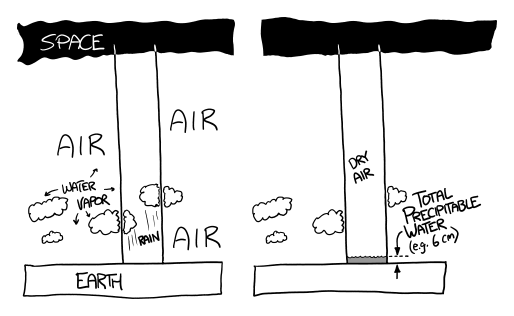
a diagram showing two views of a column connecting the ground and space. the clouds trapped in the column turn to rain, which fills up the bottom of the column.
Normally, the TPW is one or two centimeters.
Satellites measure this water vapor content for every point on the globe, producing some truly beautiful maps.
We’ll imagine our storm measures 100 kilometers on each side and has a high TPW content of 6 centimeters. This means the water in our rainstorm would have a volume of:
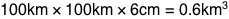
That water would weigh 600 million tons (which happens to be about the current weight of our species). Normally, a portion of this water would fall, scattered, as rain—at most, 6 centimeters of it.
In this storm, all that water instead condenses into one giant drop, a sphere of water over a kilometer in diameter. We’ll assume it forms a couple kilometers above the surface, since that’s where most rain condenses.
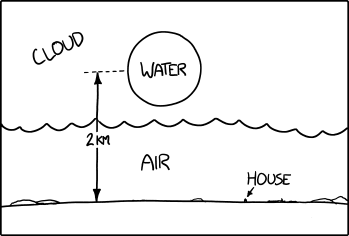
a diagram showing, from bottom to top: ground, air, cloud, and a sphere of water two kilometers up, within the cloud
The drop begins to fall.
For five or six seconds, nothing is visible. Then, the base of the cloud begins to bulge downward. For a moment, it looks a little like a funnel cloud is forming. Then the bulge widens, and at the ten-second mark, the bottom of the drop emerges from the cloud.
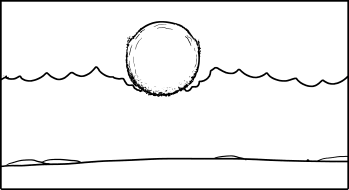
the edge of the sphere of water pokes out of the bottom of the cloud
The drop is now falling at 90 meters per second (200 mph). The roaring wind whips up the surface of the water into spray. The leading edge of the droplet turns to foam as air is forced into the liquid. If it kept falling for long enough, these forces would gradually disperse the entire droplet into rain.
Before that can happen, about 20 seconds after formation, the edge of the droplet hits the ground. The water is now moving at over 200 m/s (450 mph). Right under the point of impact, the air is unable to rush out of the way fast enough, and the compression heats it so quickly that the grass would catch fire if it had time.
Fortunately for the grass, this heat lasts only a few milliseconds because it’s doused by the arrival of a lot of cold water. Unfortunately for the grass, the cold water is moving at over half the speed of sound.

the edge of the sphere of water touches the ground
If you were floating in the center of this sphere during this episode, you wouldn’t have felt anything unusual up until now. It’d be pretty dark in the middle, but if you had enough time (and lung capacity) to swim a few hundred meters out toward the edge, you’d be able to make out the dim glow of daylight.

a person floats in darkness
As the raindrop approached the ground, the buildup of air resistance would lead to an increase in pressure that would make your ears pop. But seconds later, when the water contacted the surface, you’d be crushed to death—the shock would briefly create pressures exceeding those at the bottom of the Marianas Trench.
The water plows into the ground, but the bedrock is unyielding. The pressure forces the water sideways, creating a supersonic omnidirectional jet that destroys everything in its path.
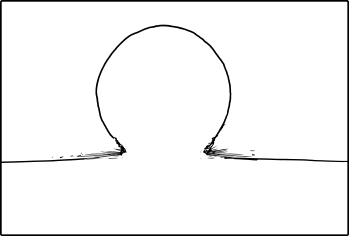
supersonic omnidirectional jets (of water) shoot out from the base of the droplet in all directions
The wall of water expands outward kilometer by kilometer, ripping up trees, houses, and topsoil as it goes. The house, porch, and old-timers are obliterated in an instant. Everything within a few kilometers is completely destroyed, leaving a pool of mud down to bedrock. The splash continues outward, demolishing all structures out to distances of 20 or 30 kilometers. At this distance, areas shielded by mountains or ridges are protected, and the flood begins to flow along natural valleys and waterways.
The broader region is largely protected from the effects of the storm, though areas hundreds of kilometers downstream experience flash flooding in the hours after the impact.
News trickles out into the world about the inexplicable disaster. There is widespread shock and puzzlement, and for a while, every new cloud in the sky causes mass panic. Fear reigns supreme as the world fears rain supreme, but years pass without any signs of the disaster repeating.
Atmospheric scientists try for years to piece together what happened, but no explanation is forthcoming. Eventually, they give up, and the unexplained meteorological phenomenon is simply dubbed a “Skrillex Storm”—because, in the words of one researcher, “It had one hell of a drop.”
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
If every person on Earth aimed a laser pointer at the Moon at the same time, would it change color?
—Peter Lipowicz
Not if we use regular laser pointers.
The first thing to consider is that not everyone can see the Moon at once. We could gather everyone in one spot, but we learned our lesson about that a few weeks ago. Instead, let’s just pick a time when the Moon is visible to as many people as possible. Since about 75% of the world’s population lives between 0°E and 120°E, we should try this while the Moon is somewhere over the Arabian Sea.
We can try to illuminate either a new moon or a full moon. The new moon is darker, making it easier to see our lasers. But the new moon is a trickier target, because it’s mostly visible during the day—washing out the effect.
Brightness aside, an ideal time would probably be 2:00 PM EST on December 27th, 2012, when a full moon will be high in the sky above Mumbai and Islamabad. At that point, the Moon will be visible to approximately five billion people—most of Asia, Europe, and Africa—about as many as can ever see it at one time.
But let’s pick a quarter moon instead, so we can see the effect on the dark side. We’ll avoid the December 21st quarter moon to avoid encouraging any Mayan nonsense, and pick the one on January 4th, 2013, half an hour after midnight (GMT). It’ll be day in East Asia but night in Africa and Europe.
Here’s our target:

the moon, half lit by light from the sun and half dark because the moon is in the way
The typical red laser pointer is about 5 milliwatts, and a good one has a tight enough beam to actually hit the Moon—though it’d be spread out over a large fraction of the surface when it got there. The atmosphere would distort the beam a bit, and absorb some of it, but most of the light would make it.

a dotted line shows that a laser pointer's beam would cover part of the moon's face
Let’s assume everyone has steady enough aim to hit the Moon, but no more than that, and the light is spread evenly across the surface.
At half an hour after midnight (GMT), everyone aims and presses the button.
This is what happens:

people aim laser pointers at the moon. there is no visible effect.
Well, that’s disappointing.
It makes sense, though. Sunlight bathes the Moon in a bit over a kilowatt of energy per square meter. Since the Moon’s cross-sectional area is around 10^13 square meters, it’s bathed in about 10^16 watts of sunlight—ten petawatts, or two megawatts per person—far outshining their five milliwatt laser pointer. There are varying efficiencies in each part of this system, but none of it changes that basic equation.

a man in a hat suggests trying more power.
5 milliwatts is wimpy. We can do better.
A 1-watt laser is an extremely dangerous thing. It’s not just powerful enough to blind you—it’s capable of burning skin and setting things on fire. Obviously, they’re not legal for consumer purchase in the US.
Just kidding! You can pick one up for $300.
So suppose we spend the $2 trillion to buy one-watt green lasers for everyone. (Memo to presidential candidates: this policy would win my vote.) In addition to being more powerful, green laser light is nearer to the middle of the visible spectrum, so the eye is more sensitive to it and it seems brighter.
Here’s the effect:

people aim more powerful laser pointers at the moon. there is no visible effect.
Dang.
The laser pointers we’re using put out about 150 lumens of light (more than most flashlights) in a beam 5 arc-minutes wide. This lights up the surface of the Moon with about half a lux of illumination—compared to about 130,000 lux from the sun. (Even if we aimed them all perfectly, it would only manage half a dozen lux over about 10% of the Moon’s face.)
By comparison, the full moon lights up the Earth’s surface with about one lux of illumination—which means that not only would our lasers be too weak to see from Earth, but if you were standing on the Moon, the laser light on the landscape would be fainter than Moonlight is to us on Earth.

a man in a hat suggests trying more power.
With advances in lithium batteries and LED technology over the last ten years, the high-performance flashlight market has exploded. But it’s clear that flashlights aren’t gonna cut it. So let’s skip past all of that and give everyone a Nightsun.
You may not recognize the name, but chances are you’ve seen one in operation: It’s the searchlight mounted on police and Coast Guard helicopters. With an output on the order of 50,000 lumens, it’s capable of turning a patch ground from night to day.
The beam is several degrees wide, we’ll want some focusing lenses to get it down to the half-degree needed to hit the Moon.
Here’s the effect:

people aim Nightsuns at the moon. there might be a visible effect. it's hard to say.
It’s hard to see, but we’re making progress! The beam is providing 20 lux of illumination, outshining the ambient light on the night half by a factor of two! However, it’s quite hard to see, and it certainly hasn’t affected the light half.

a man in a hat suggests trying more power.
Let’s swap out each Nightsun for an IMAX projector array—a 30,000-watt pair of water-cooled lamps with a combined output of over over a million lumens.

people aim IMAX projectors with lenses on them at the moon. there's little visible effect.
Still barely visible.

a man in a hat suggests trying more power.
At the top of the Luxor Hotel in Las Vegas is the most powerful spotlight on Earth. Let’s give one of them to everyone.

a battery of luxor hotels fires beams of light at the moon. the light is slightly visible on the dark side.
Oh, and let’s add a lens array to each so the entire beam is focused on the Moon:

a battery of luxor hotels with lenses fires beams of light at the moon. the dark side is visibly illuminated.
Our light is definitely visible, so we’ve accomplished our goal! Good job, team.

a man in a hat suggests trying more power.
… Well.
The Department of Defense has developed megawatt lasers, designed for destroying incoming missiles in mid-flight.
The Boeing YAL-1 was a megawatt-class chemical oxygen iodine laser mounted in a 747. It was an infrared laser, so it wasn’t directly visible, but we can imagine building a visible-light laser with similar power. Let’s give one to everyone.

a fleet of aircraft fire megawatt lasers at the moon. the dark side is nearly as bright as the light side.
Finally, we’ve managed to match the brightness of sunlight!
We’re also drawing five petawatts of power, which is double the world’s average electricity consumption.

a man in a hat suggests trying more power.
Ok, let’s mount a megawatt laser on every square meter of the surface of Asia. Powering this array of 50 trillion lasers would use up Earth’s oil reserves in approximately two minutes, but for those two minutes, the Moon would look like this:

a field of megawatt lasers covering asia fires at the moon
The Moon shines as brightly as the midmorning sun, and by the end of the two minutes, the lunar regolith is heated to a glow.

a man in a hat suggests trying more power.
Ok, let’s step even more firmly outside the realm of plausibility.
The most powerful laser on Earth is the confinement beam at the National Ignition Facility, a fusion research laboratory. It’s an ultraviolet laser with an output of 500 terawatts. However, it only fires in single pulses lasting a few nanoseconds, so the total energy delivered is about equivalent to a quarter-cup of gasoline.
Let’s imagine we somehow found a way to power and fire it continuously, gave one to everyone, and pointed them all at the Moon. Unfortunately, the laser energy flow would turn the atmosphere to plasma, instantly igniting the Earth’s surface and killing us all.
But let’s assume that the lasers somehow pass through the atmosphere without interacting.
Under those circumstances, it turns out Earth still catches fire. The reflected light from the Moon would be four thousand times brighter than the noonday sun. Moonlight would become bright enough to boil away Earth’s oceans in less than a year.
But forget the Earth—what would happen to the Moon?
The laser itself would exert enough radiation pressure to accelerate the Moon at about one ten millionth of a gee. This acceleration wouldn’t be noticeable in the short term, but over the years, it adds up to enough to push it free from Earth orbit.
… If radiation pressure were the only force involved.
40 megajoules of energy is enough to vaporize a kilogram of rock. Assuming Moon rocks have an average density of about 3 kg/liter, the lasers would pump out enough energy to vaporize four meters of lunar bedrock per second:
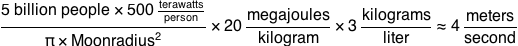
However, the actual lunar rock won’t evaporate that fast—for a reason that turns out to be very important.
When a chunk of rock is vaporized, it doesn’t just disappear. The surface layer of the Moon becomes a plasma, but that plasma is still blocking the path of the beam.
Our laser keeps pouring more and more energy into the plasma, and the plasma keeps getting hotter and hotter. The particles bounce off each other, slam into the surface of the Moon, and eventually blast away into space at a terrific speed.
This flow of material effectively turns the entire surface of the Moon into a rocket engine—and a surprisingly efficient one, too. Using lasers to blast off surface material like this is called laser ablation, and it turns out to be a promising method for spacecraft propulsion.
The Moon is massive, but slowly and surely the rock plasma jet begins to push it away from the Earth. (The jet would also scour clean the face of the Earth and destroy the lasers, but we’re pretending for the moment that they’re invulnerable.) The plasma also physically tears away the lunar surface, a complicated interaction that’s tricky to model.
But if we make the wild guess that the particles in the plasma exit at an average speed of 500 kilometers per second, then it will take a few months for the Moon to be pushed out of range of our laser. It will keep most of its mass, but escape Earth’s gravity and enter a lopsided orbit around the sun.
Technically, the Moon won’t become a new planet, under the IAU definition of a planet. Since its new orbit crosses Earth’s, it will be considered a dwarf planet like Pluto. This Earth-crossing orbit will lead to periodic unpredictable orbital perturbation. Eventually it will either be slingshotted into the Sun, ejected toward the outer Solar System, or slammed into one of the planets—quite possibly ours. I think we can all agree that in this case, we’d deserve it.
Scorecard:

everyone fires 500-terawatt lasers at the moon. the moon leaves.
And that, at last, is enough power.
every night you would come into my bed after everyone was asleep and we would simply cuddle, hug, and be happy like that.
In today’s article, I give short answers to several reader questions.
How long would the Sun last if a giant water hose were focused upon it? My sixth grade brother, Adam, asked me this.
—Austin Dickey
Your brother might be surprised to learn that the water would actually make the Sun hotter!
austin's sixth grade brother, adam, waters the sun
Water is made of hydrogen and oxygen, which is fuel for the Sun’s fusion. But more importantly, the extra mass also makes the Sun heavier. This crushes it together more tightly and makes fusion happen faster. This means it will burn more brightly and run through its fuel more quickly.
As you keep adding water, the Sun will go through a lot of wacky fusion phases. (During one phase, called a helium flash, the reaction rate is proportional to the 40th power of the temperature—which is probably the largest exponent I’ve ever seen in a physics equation!)
But one way or another, eventually the whole thing will collapse in on itself, blow off its outer layers, and become a black hole. This black hole will keep soaking up water, spraying off X-rays in the process, until finally the municipal water department notices what you’ve been doing and shuts off your service.
What if you shined a flashlight (or a laser) into a sphere made of one-way mirror glass?
—Chase Montgomery
Believe it or not, you’ve been lied to all your life—there’s no such thing as one-way mirror glass.
Glass either lets light through or reflects it, but there’s no glass that lets light through one way and reflects it the other way. The glass in police shows is partially reflective (on both sides). The key is that the room on the prisoner’s side is brightly lit, so the reflection washes out the small amount of light from the observers’ side.
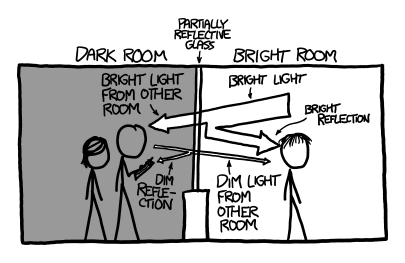
two people in a dark room look through one way glass at one person in a light room.
If Michael Phelps could hold his breath indefinitely, how long would it take for him to reach the lowest point in the ocean and back if he swam straight down and then straight back up?
—Jimmy Morey
He’d most likely black out and die somewhere between 100 and 400 meters.

michael phelps is unable to swim upward because his gold medals are too heavy.
The human body handles pressure remarkably well. With the right preparation, we can survive pressures over a dozen atmospheres. Different body systems break down at different depths, but one of the trickiest limits is created by High Pressure Nervous Syndrome. Below about 100 meters, divers become jittery and excitable (especially if the pressure increase is rapid), and at the same time begin slipping in and out of sleep. The reason may be direct pressure on the brain.
But let’s suppose Michael Phelps were immune to all those things. In that case, it simply becomes a question of speed.
There aren’t very many records for underwater swimming, but based on how quickly this guy completed the 50m backstroke, it would probably take Michael about ...
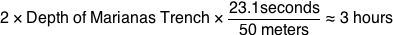
… to make the trip.
In the first Superman movie, Superman flies around Earth so fast that it begins turning in the opposite direction. This somehow turns back time [... ] How much energy would someone flying around the Earth have to exert in order to reverse the Earth's rotation?
—Aidan Blake
Someone recently blew my mind by telling me I’d been misinterpreting that scene all my life. I like their take on it way better:
Superman wasn't exerting a force on the Earth. He was just flying fast enough to go back in time. (Faster than light, I guess? Comic book physics.) The Earth changed direction because we were watching time run backward as he traveled. It didn't actually have anything to do with the direction he was flying.
Now that I see it, it makes a lot more sense. I mean, as much sense as a red-cape-and-outside-underwear time traveler can make.
A discussion of the reversal of the Earth’s spin—and what that even means—will have to wait for another article.
How fast would you have to go in your car to run a red light claiming that it appeared green to you due to the Doppler Effect?
—Yitzi Turniansky
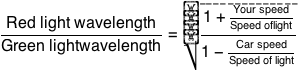
What would happen if you opened a portal between Boston (sea level) and Mexico City (elev. 8000+ feet)?
—Jake G.
Bernoulli’s principle gives us this estimate of the air flow rate:

That’s fast enough to strip up the pavement from a parking lot. I suggest we put it in Kendall Square—the MIT folks are probably used to dealing with this kind of thing.
When my wife and I started dating she invited me over for dinner at one time. Her kitchen had something called Bauhaus chairs, which are full of holes, approx 5-6 millimeters in diameter in both back and seat. During this lovely dinner I was forced to liberate a small portion of wind and was relieved that I managed to do so very discretely. Only to find that the chair I sat on converted the successful silence into a perfect, and loud, flute note. We were both (luckily) amazed and surprised and I have often wondered what the odds are for something like that happening. We kept the chairs for five years but despite laborious attempts it couldn't be reproduced.
—R. D.
This ... isn’t actually a question.

i don't know how all these words got on my screen.
But thank you for sharing!
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
What if you exploded a nuclear bomb (say, the Tsar Bomba) at the bottom of the Marianas Trench?
—Evin Sellin
Surprisingly little—especially compared to what would happen if you put it just under the surface.
Evin isn’t the first person to think of setting off nuclear weapons underwater. In fact, we’ve actually tried it a bunch of times. This is what it looks like.
Most of the tests, however, involved either small bombs or shallow water. Evin’s scenario concerns neither.
At 53 megatons, the Tsar Bomba was the most powerful nuclear weapon ever detonated, and at 11 kilometers, the Mariana(s) Trench is the deepest part of the ocean. No underwater test has involved bombs anywhere near that size, nor depths anywhere near that deep.
In 1962, physicist Freeman Dyson wrote a memo discussing eight possible novel weapon systems, all of which looked like they’d be possible in the near future, and outlined the potential military uses and dangers of each. This memo has been declassified, but was never published. Freeman’s son, science historian George Dyson, got a paper copy of the memo from his father, and was kind enough to show it to me.
In the memo, one of the eight ideas Freeman discusses is the use of gigaton nuclear weapons as wave generators. It includes this rather terrifying passage describing the detonation of a submerged gigaton mine off the North American coast: “Quantitative study of the destructive effects has not been made. Rough estimates indicate that the inundation would reach to a height of 200-300 feet above sea level, or a distance of 200-300 miles inland, whichever limit is reached first.”
a map showing a thing happening in the atlantic ocean and then another thing happening to the east coast of north america
Luckily for the coast, later research paints a less dire picture.
The seminal work in the field of nuclear ocean waves is Water Waves Generated By Underwater Explosions, a sprawling 400-page report produced for the Department of Defense by Bernard Le Mehaute and Shen Wang. The report, published in 1996, exhaustively examines and summarizes all available research about the ocean waves created by nuclear explosions.
The report outlines how when a nuclear weapon goes off underwater, it produces a cavity of hot gasses, which then collapses. If the explosion happens near the surface, it can create some pretty big waves—under some circumstances, they can be hundreds of feet high near ground zero.
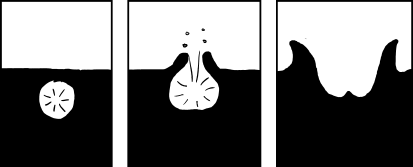
a bubble forms and rises out of the water, creating waves.
Or is it ocean zero?
Fortunately for the coast, these waves are fundamentally different from tsunamis. It turns out that if the waves are very large, they break early, and expend most of their energy creating a narrow surf zone on the continental shelf. This is potentially hazardous to some ships, but much less catastrophic than a direct nuclear attack. When they reached the coast, the waves would be no worse than those from a bad storm.
But those are waves from an explosion close to the surface. A nuke set off deep underwater acts a bit differently.
The explosion at the bottom of the Mariana Trench will create a quickly-expanding spherical cavity of hot steam. To figure out how big it gets, we can try a formula from the 1971 paper Evaluation of Various Theoretical Models For Underwater Explosion:
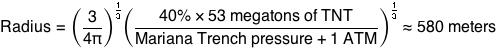
The bubble grows to about a kilometer across in a couple of seconds. The water above bulges up, though only slightly, over a large area. Then the pressure from that six miles of water overhead causes it to collapse. Within a dozen or so seconds, the bubble shrinks to a minimum size, then ‘bounces’ back, expanding outward again.
It goes through three or four cycles of this collapse and expansion before disintegrating into, in the words of the 1996 report, “a mass of turbulent warm water and explosion debris.” According to the report, as a result of such a deep-water closed bubble creation and dissipation, “no wave of any consequence will be generated.”
That “turbulent warm water” is actually quite substantial. The rising column of heat creates a hot spot in the ocean—many degrees warmer than the surrounding water—that lingers for some time.

tropical cyclone passes over the mariana trench
Earlier this year, Severe Tropical Storm Sanvu passed over the Mariana Trench. The column of deep, hot water from our nuke could conceivably have been enough to strengthen it into a typhoon, much as the deep warm waters of the Gulf of Mexico’s Loop Current sometimes cause hurricanes to rapidly intensify. In addition to the heat energy from the water, Sanvu could whip up a spray containing fallout from the blast, and approach Iwo Jima as a radioactive whirlwind.
Of course, that’s getting a little far-fetched. In the absence of an improbable typhoon interaction, the overall effect of the bomb isn’t quite as dramatic as Evin might have imagined.
... But.
All that changes when this cat enters the equation:

a man in a hat holds up a cat
Literally.
Let’s say that when I’m typing the above equation, the cat hops onto my desk and steps on the “0” key, which inserts six extra zeroes:
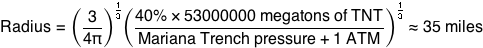
If there was enough water, and if the model held up, this blast would expand into a bubble 70 miles across.
In reality, the oceans aren’t that deep. Instead, it blows a hole in the Earth’s crust dozens of miles across, leaving a hole through which briefly glows the magma of the mantle.
Around the early 1990s, scientists started discovering jumbled fields of petrified wood mixed with sand buried beneath the Louisiana and Texas coast. These turned out to be the remains of North American forests swept out to sea by a massive tsunami. The culprit was a comet or asteroid hitting the Yucatan—the impact that killed most of the dinosaurs. The debris played a key role in identifying the 65-million-year-old Chicxulub impact site—this book provides a wonderful account of the unraveling of that mystery.
53,000,000 megatons is approximately the energy of the Chicxulub impact. A blast this size in the Mariana Trench creates kilometer-high waves that engulf the forests of Indonesia, California, and the Pacific Northwest, along with most of coastal China and the rest of the Pacific rim.
Huge volumes of rock and water are blasted into space. The debris takes less than an hour to encircle the Earth. As the chunks of rock fall back into the atmosphere, they heat to a glow—like meteors—igniting global firestorms. The hole fills in, with huge columns of steam and great convulsions.
The Mariana Trench is gone, and with it Guam and the Mariana Islands. The area is now marked by a 100-kilometer-wide scar of magma sizzling beneath the waters of the Pacific.
The majority of the world’s plants die and the food chain collapses completely. Between the famine and the fires, most life on Earth is wiped out.
Stupid cat.

the cat which just destroyed the planet licks its paw
i like you
How dangerous is it, really, to be in a pool during a thunderstorm?
—Jay Gengelbach
What would happen if you were taking a shower when you were struck by lightning? Or standing under a waterfall?
—same3chords
What would happen if you were in a boat or a plane that got hit by lightning? Or a submarine?
—SoobNauce
What if you were changing the light at the top of a radio tower and lightning struck? Or what if you were doing a backflip? Or standing in a graphite field? Or looking straight up at the bolt?
—Danny Wedul
What would happen if lightning struck a bullet in midair?
—Timothy Campbell
What if you were flashing your BIOS during a thunderstorm and you got hit by lightning?
—njsg
Before we go any further, I want to emphasize something:
I am not an authority on lightning safety. I am a guy who draws pictures on the internet. I like when things catch fire and explode, which means I do not have your best interests in mind. The authorities on lightning safety are the folks at the US National Weather Service:
http://www.lightningsafety.noaa.gov/
Ok. With that out of the way ...
To answer these questions, we need to get an idea of where lightning is likely to go. There’s a cool trick for this, and I’ll give it away right here at the start: Roll an imaginary 60-meter sphere across the landscape and look at where it touches.
They say lightning strikes the tallest thing around. That’s the kind of maddeningly inexact statement that immediately sparks all kinds of questions. How far is “around”? I mean, not all lightning hits Mt. Everest. But does it find the tallest person in a crowd? The tallest person I know is probably Ryan North (paleontologists estimate he stood nearly five meters tall at the shoulder). Should I try to hang around him for lightning safety reasons? What about other reasons? (This is probably why you people ask the questions on this blog, not me.)
But how does lightning pick its targets?
This video, captured by Tom A. Warner, might be the single coolest piece of footage I’ve ever seen. It shows a bolt of lightning recorded at 7,207 frames per second. The 33-second video represents barely a tenth of a second of real time. There are lots of slow-motion videos of lightning, but this is by far the best I’ve found.
Tom’s video gives an idea of how lightning moves. It starts with a branching bundle of charge—the “leader”—descending from the cloud. This is what you see in the first part of the video. It spreads downward at speeds of tens to hundreds of kilometers per second, covering the few kilometers to the ground in a few dozen milliseconds.
The leader carries comparatively little current—on the order of 200 amps. That’s still enough to kill you, but it’s nothing compared to what happens next. Once the leader makes contact with the ground, the cloud and the ground equalize with a massive discharge of more like 20,000 amps. This is the blinding flash you see. It races back up the channel at a significant fraction of the speed of light, covering the distance in under a millisecond—all within a single frame of that video.
(Technical detail: while it’s called a “return stroke”, charge is still flowing downward. However, the discharge appears to propagate upward. This effect similar to how when a traffic light turns green, or whatever color, the cars in front start moving, then the cars in back, so the movement appears to spread backward.)
So the place on the ground where we see a bolt “strike” is the spot where the leader first makes contact with the surface. The leader moves down through the air in little jumps. It’s ultimately feeling its way toward the (usually) positive charge in the ground. However, it only “feels” charges within a few tens of meters of the tip. If there’s something connected to the ground within that distance, the bolt will jump to it. Otherwise, it jumps out in a semi-random direction and repeats the process.
lightning makes a series of steps down toward ryan north
This is where the 60-meter sphere comes in. It’s a way to imagine what spots might be the first thing the leader senses—the places it might jump to in its next (final) step.
To figure out where lightning is likely to hit, you roll the imaginary 60-meter sphere across the landscape (for safety reasons, do not use a real sphere). This sphere climbs up over trees and buildings without passing through anything (or rolling it up). Places the surface makes contact—treetops, fenceposts, and golfers in fields—are potential lightning targets.
This means you can calculate a lightning “shadow” around an object of height h on a flat surface.
a sphere of radius 30 meters rests on the ground next to a man on a platform with a flag
The shadow is the area where the leader is likely to hit the tall object instead of the ground around it:

Now, that doesn’t mean you’re safe on the ground around it—often, it means the opposite. After the current hits the tall object, it flows out into the ground. If you’re touching the ground nearby, it can travel through your body. Of the 28 people killed by lightning so far this year, 13 were standing under or near trees.
With all this in mind, let’s look at possible lightning paths for the scenarios in the questions.
How dangerous is it, really, to be in a pool during a thunderstorm?
Pretty dangerous. Water is conductive, but that’s not the biggest problem—the biggest problem is that if you’re swimming, your head is poking up from a large flat surface. But lightning striking the water near you would still be bad. The 20,000 amps spread outward—mostly over the surface—but how much of a jolt it will give you at what distance is hard to calculate
My guess is that you’d be in significant danger anywhere within a minimum of a dozen meters—and further in fresh water, because the current will be happier to take a shortcut through you.
What would happen if you were taking a shower when you were struck by lightning? Or standing under a waterfall?
lightning strikes two people, one standing in an inside waterfall and one standing in an outside waterfall
You’re not in danger from the spray—it’s just a bunch of droplets of water in the air. It’s the tub under your feet, and the puddle of water in contact with the plumbing, that’s the real threat.
What would happen if you were in a boat or a plane that got hit by lightning? Or a submarine?

lightning hits a boat, another boat, and a plane. it does not hit the submarine because the ocean is in the way.
A boat without a cabin is about as safe as a golf course. A boat with a closed cabin and a lightning protection system is about as safe as a car. A submarine is about as safe as a submarine safe (a submarine safe is not to be confused with a safe in a submarine—a safe in a submarine is substantially safer than a submarine safe).
What if you were changing the light at the top of a radio tower and lightning struck? Or what if you were doing a backflip? Or standing in a graphite field? Or looking straight up at the bolt?

lightning strikes a person on a tower, then flows into the tower to the ground. another bolt passes through someone doing a backflip. a person stands in a graphite field (?). a person looks at a lightning bolt which is hitting them in the eyes.
What would happen if lightning struck a bullet in midair?
The bullet won't affect the path the lightning takes. You'd have somehow to time the shot so the bullet was in the middle of the bolt when the return stroke happened.
The core of a lightning bolt is a few centimeters in diameter. A bullet fired from an AK-47 is about 26 mm long and moves at about 700 millimeters every millisecond.
The bullet has a copper coating over a lead core. Copper is a fantastically good conductor of electricity, and much of the 20,000 amps could easily take a shortcut through the bullet.

a bullet passes through the ionized channel of a lightning bolt. as it reaches the center, it glows very brightly. it is still going brightly as the bullet exits undamaged.
Surprisingly, the bullet handles it pretty well. If it were sitting still, the current would quickly heat and melt the metal. But it’s moving along so quickly that it exits the channel before it can be warmed by more than a few degrees. It continues on to its target relatively unaffected. There are some curious electromagnetic forces created by the magnetic field around the bolt and the current flow through the bullet, but none of the ones I examined changed the overall picture very much.
What if you were flashing your BIOS during a thunderstorm and you got hit by lightning?
the tempest installs microsoft bob (gateway 2000 edition)
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
If cows could photosynthesize, how much less food would they need?
—Anonymous
In a way, they already do. A field of grass sits there all day soaking up energy from the sun and storing it chemically. A grazing animal can then come along and absorb weeks of accumulated energy in a matter of minutes.

cows absorbing energy
A Jersey cow presents in the neighborhood of nearly two square meters of usable space to the sun if it stands right. (Cows would have to be trained to stand optimally, but we might not have too far to go; research suggests they already align themselves north-south.
Chlorophyll photosynthesis extracts 3%-6% of the total energy from sunlight. If we figure on any given day the cow gets the equivalent of about six hours of peak sunlight, it works out to less than two million joules of usable energy each day.
grass giving cows energy
Is that a lot? Well, a 450-kilogram cow just wandering around in a field might eat about 10 kilograms of dry matter a day, extracting on the order of 50 million joules of metabolic energy. So photosynthesis could only make up about 4% of the required intake—saving only a few handfuls of grain.
If we could equip cows with solar panels, which can be several times more energy-efficient than photosynthesis, we could improve that number—but not by much.
cow with a solar panel on its back
The basic problem facing cows is the same one facing solar cars—they're too small. If you saw the world's cattle population in silhouette, they'd have an overall cross-sectional area of about two thousand square kilometers. This means that if they were migrating through the air over Rhode Island (biology is not my strong suit), they'd blot out the sun over barely half the state. They'd only catch enough sunlight to produce a daily average of about 40 gigawatts of power (two megayodas).
By contrast, about 3% of the world's surface area is cultivated, which means that (given rough estimates of geographic distribution of farmland) our crops easily intercept over a thousand times more sunlight than our cattle—which is why grazing is a good strategy.
I'd like to conclude with this quote, which I found in the Cedara Agricultural Development Institute's Applied Ruminant Nutrition for Dairy Cows:
Cows on a typical dairy ration can produce 80 to 100 litres of saliva per day.
This has nothing to do with photosynthesis, but I wanted to share anyway.
bottles... of cow saliva... ew.
we went to telica and slept under the stars, to asososca and swam in the lagoon, i liked you, i was shy, i just wanted to talk to you all day and kiss you all night
In Armageddon, a NASA guy comments that a plan to shoot a laser at the asteroid is like “shooting a b.b. gun at a freight train.” What would it take to stop an out-of-control freight train using only b.b. guns?
—Charles James O'Keefe
First of all, for the record, shooting asteroids with lasers is a great way to deflect them. Stopping a train with a BB gun might be harder.
A Red Ryder spring-piston lever-action air rifle fires a standard 0.177-caliber 0.33g steel BB at a muzzle velocity of 100 meters per second.
The GE Genesis Series I locomotive weighs 12 metric tons and travels at around 45 meters per second.
If you bounce a single BB off the front of the locomotive from point blank range, you slow it down by about a foot per day.

someone with a bb gun shoots an eye out
At one shot per second, it’d take over two days and nearly 200,000 BBs to bring the train to a halt—and by that point it would’ve stopped on its own anyway. (Based on the formulas on this page for the drag forces on a train, a back-of-the-envelope differential equation for the locomotive's motion suggests that on a flat track with no brakes, it would slow down on its own from 100 to 20 mph in ten or fifteen minutes).
Clearly, the Red Ryder isn’t cutting it.
It’s time to wade into the terrifying world of hardcore air rifle enthusiasts.
The Tactical Edition Drozd Blackbird is a high-end BB machine gun (of course there are BB machine guns). It fires 1200 rounds a minute at a muzzle velocity of over 200 meters per second. At those speeds, standard BBs are capable of fracturing bone.
Unfortunately, even instantaneously emptying the full 600 rounds into the front of the train would only reduce its speed by a small fraction of a percent.
A single person with a BB gun can't do it. But what if we had an army?

a ragtag band of misfits holds bb machine guns
We’ll give each person a patch of ground two feet by four feet. This is a little cramped, but it should give them room to fire in an arc over the shoulder of the person in front of them. If we restrict them to 45 degrees in front of the train on either side of the track, we can pack about 100 people within 10 meters, 300 more within 20 meters, 550 more within 30 meters, and another 750 within 40 meters.
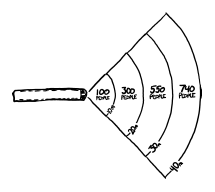
a diagram shows how various numbers of people are arranged in front of the train they are going to shoot at with bb guns
Most of the shooters are able to hit the train fairly straight-on. Integrating the momentum from all the different shooting angles shows that the fanned-out arrangement exerts on the train over 90% of the force that an ideal arrangement (with every gun directly in front of the train) would.
BBs experience a lot of drag, so the shots from those further away will reach the train at a lower speed. This page gives estimates for the drag forces on a BB at various speeds. I love the internet.
With all that in mind, let’s look at what happens when a crowd of people with BB machine guns try to stop a train. In fact, people have two arms, so let’s have them all dual-wield.
At t=0, the people within 50 meters of the train—all 2,500 of them—pull the triggers, unleashing 100,000 BBs per second. As the train plows ahead, people in front magically fly sideways off the tracks. This is unrealistic, but we can’t let them slow down the train with their bodies—that would be cheating.
As those people stop firing, people further down the tracks come into range and start shooting. The train is moving so quickly that any one person only gets off a few dozen rounds before the target moves past (or through) them.
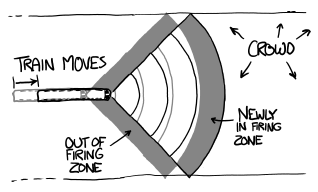
a diagram shows how when the train moves forward different people are able to shoot at it
At any given time, there are 45,000 BBs in the air. But there’s a problem: When the steel balls bounce off the front of the train, they don’t disappear. They fly back at the shooters (who’ll probably shoot their eyes out) and into the line of fire. At its peak, this cloud of ricochets deflects nearly 1% of incoming shots via BB-BB collisions. This is a neat effect, but it doesn’t substantially interfere with our operation.
Unfortunately, even this hail of steel takes several excruciating minutes—and almost two kilometers of track—to stop the train. That means we’d need over 100,000 shooters lined up along the track, and arming them would cost in the neighborhood of $50 million.
We can do better, but we’ll have to relax the BB gun requirement.
The AK-47 has a muzzle velocity of 715 meters per second and fires a bullet which outweighs a steel BB by a factor of 25. The bullets go so fast that they penetrate into the body of the train (which means they’re a little less efficient at transferring momentum, but it doesn’t really matter).
Calculations show a crowd of 2,500 people firing two AK-47s each would be able to stop our runaway locomotive within the space of 30 meters—in only a second and a half. Mission accomplished.

a man in a hat suggests we try more
... well.
The greatly reduced drag coefficient of machine gun ammo compared to steel ball bearings means we can shoot from a much greater distance. Let’s make the crowd 200 meters deep instead of 50.
At t=0, 40,000 people open fire. The AK-47 typically has a 30-round magazine and fires 10 shots per second. Within a third of a second, a quarter of a million bullets are in the air. Stray shots no doubt cause a lot of fatalities in the front of the crowd, but with a trained and disciplined group of shooters, the bulk of the shots could actually manage to hit the target.
At t=15 ms, the locomotive has inched forward by half a meter and encounters the leading edge of the bullet cloud.
By t=30 ms, the locomotive is being hit by a half dozen new bullets every millisecond.
At t=150 ms, the locomotive has crawled forward about six meters, but it’s absorbing several hundred bullets each millisecond. This has begun to slow its forward momentum (and tear it apart—let’s assume it’s loaded full of some kind of lightweight material that distributes the shock of the bullet evenly).
At around t=300ms, the full quarter of a million bullets are in the air. Most people have gotten off a total of six shots between their two guns. Interestingly, the bullets from the front rows of shooters occasionally catch up with—and collide with—slower bullets from the shooters behind them. This doesn’t happen a lot, but it does happen.
The locomotive creeps forward to seven meters, seven and a half, seven and three quarters … and then seven and a half again.
Success.
But the shooters have only fired about a dozen rounds so far. Their magazines are still mostly full.
At t=1s, almost a million shots have been fired. The locomotive is sliding backward at about 100 m/s (220 mph). At t=2s, the locomotive’s backward acceleration slows down quite a bit. This is partly because it’s starting to get out of range of the shooters. But it’s also because the locomotive is traveling at nearly the speed of sound, and the bullets are having a harder and harder time catching up. When they do, they have so little relative velocity that they can’t accelerate it much more.
By this point, drag from the atmosphere is the dominant force on the locomotive’s motion. The rear end lifts from the tracks, the locomotive starts to tumble, and finally disintegrates into a cloud of shrapnel and spent bullets.
Now bring on that asteroid.

an asteroid approaches a planet which is excited about shooting lasers at it
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
What if there's LITERALLY a tie?
—Nate Silver (Twitter, January 4th, 2012)
In most states, a popular vote tie is broken by a coin toss or drawing names from a hat. The odds of a many-state tie are slimmer than the odds of the hat being hit by a bale of cocaine dumped from a drug-smuggling airplane.
Nate Silver flippantly posted his 'tie' question on Twitter during the tallying of the extremely close 2012 Republican Iowa Caucus results. In that case, an exact tie was averted—Santorum ended up winning by 34 votes out of 121,503. And since it was a non-binding nominating vote, the Iowa Republican Party could handle a tie any way they wanted.
But since it’s Election Day, let’s apply his question to the current contest. What will happen if there's a tie?
I don't mean an electoral college tie. There’s probably about a 1 in 500 chance of one of those this year, and the consequences are thoroughly explored. Instead, the question concerns both candidates getting the same number of votes in a state.
Several researchers—including Silver himself—have calculated the odds of a state winner being decided by a single vote, which is effectively the same as the probability of a tie vote. For typical close states, the linked article calculates the probabilities to be in the neighborhood of 1 in 100,000—which makes intuitive sense, since 100,000 is the sort of vote margin by which swing state elections are typically decided.
So what if there's a tie in a close state this year?
a map showing florida tied and all other states going as nate silver currently projects
For that matter, what if there’s a tie in every battleground state?
a map showing all battleground states tied
Well, for starters, recounts happen. But since recounts happen in close elections in general, these are just as likely to create ties as to break them. They don’t change the underlying probability. So let’s assume that after all recounts, there’s a tie. What then?
The short answer is that it’s up to the state’s laws.
I went through the general laws of nine competitive states to see how they handle popular vote ties. In most of them, the tie is broken by “drawing lots”—that is, randomly. (If you’re curious, here are links to some tie vote laws in each state: Virginia, North Carolina, Florida, Ohio, New Hampshire, Wisconsin, Colorado, Iowa, Nevada).
a secretary of state flips a coin
“Drawing lots” can mean a coin toss, drawing straws, or picking a name from a hat. Most states leave the details up to the Secretary of State or an electoral board, although Iowa Code 50.44 specifies that the names be written on pieces of paper and placed in a “receptacle”. In North Carolina, however, a tie vote (when more than 5,000 votes are cast) results in a new election. (Which could potentially itself result in a tie ...)
But let’s imagine that there’s not just one state that’s tied—instead, the nine most competitive states are tied (and the rest go as expected). If North Carolina held a runoff to break the tie, and the other eight states flipped coins (or picked from Iowa’s receptacle), Obama would be reelected in 431 out of 512 cases—about 84% of the time.
But how likely is a nine-state tie?
If we ballpark the odds of a tie vote in each close state at 1 in 100,000, then the odds of a tie vote in all nine states is in the neighborhood of one in a quattuordecillion—1 followed by 45 zeroes. (This ignores vote correlation between states, but it’s good enough for a first-order estimate).
Florida is hit by an average of 66 tornadoes per year. If each tornado is 50 yards wide and has a path 1.5 miles long (which is typical, if not necessarily the mean), we can calculate that a typical location in Florida experiences an average 1.4 picotornados per second:
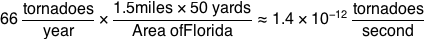
Astronomer Alan Harris calculates that a person’s lifetime odds of death from a comet or meteorite impact are about 1 in 700,000. If a typical person in the calculation lives 70 years, this suggests a Florida resident suffers an average of 0.64 femtodeaths per second from meteorite impacts:
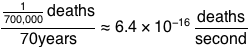
In 1994, drug smugglers fleeing the authorities dropped an estimated 20 bales of cocaine from an airplane over Florida—one of which crashed through the roof of a Crime Watch meeting and narrowly missed the Homestead Chief of Police. If Florida has been hit by 20 bales of cocaine over the last 20 years, then the average person in Florida is struck by an average of 29 zeptobales of cocaine per second:

(By the way—this means that given a street price of $20,000 per
kilogram, a typical acre of Florida land produces an average revenue of
three cents per year in falling cocaine bales).
Putting all this together: The probability that every battleground state is exactly tied is roughly equal to the probability that, when one of the Florida electors reaches into the hat to draw a name, he or she is struck by a falling cocaine bale, the hat is hurled away within the next few seconds by a tornado, and the elector is obliterated minutes later by a meteorite impact.
this is still more likely than ron paul winning
If you’re in the US, don’t forget to vote—your vote could make or break a tie.
And if you’re voting in Florida, keep an eye on the sky.
and then, you asked me to write in your journal. i told you that i thought you were a beautiful person and that the mere fact of knowing you made me a better person. you offered me a croissant, and i left. it didn't feel like we were over
"If a meteor made out of diamond and 100 feet in diameter was traveling at the speed of light and hit the earth, what would happen to it?”
—Aidan Smith, Age 8, via his father Jeff
Nothing made of matter can go at the speed of light. But that’s ok—we can get close enough!
No matter how fast you push something, it will never quite get up to light speed. This seems like it can’t be right, but it is. Our universe has some weird rules. But the closer something gets to the speed of light, the more energy and momentum it has—and this energy and momentum go up without limit.
We’ll start slow and work our way up.
1 kilometer per second:
If we drop the meteor from the edge of space, 100 kilometers up, it’ll punch through the atmosphere without slowing down too much and hit the ground moving about Mach 3—over a kilometer a second.
As it falls, it compresses the air in front of it. When the air is compressed, it heats it up. (This is the same thing that heats up spacecraft and meteors—actual air friction has little to do with that.) By the time it reaches the ground, the lower surface will have heated to over 500℃, which is enough to glow visibly.
When it hits the ground, two minutes after it was released, it makes a crater 300 meters across—the size of a school, shattering into fragments in the process.

there was a school here once
11 kilometers per second:
If we set the diamond in space a little ways away from the Earth, and let it fall toward us, it will hit at about 11 kilometers per second. This is Earth’s escape velocity, and anything that hits the Earth from space will—thanks to gravity—be going at least that fast.
At 11 kilometers per second, the brief descent would be visible as a fireball. The energy of the impact would be comparable to a small atomic bomb, and the crater it would create would be a kilometer across—a little smaller than Meteor Crater in Arizona.
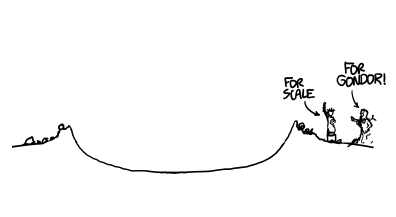
FOR- MATTING
72 kilometers per second:
This is just about the fastest that anything can hit the Earth if it’s orbiting the Sun. The Leonid meteor shower hits at this speed.
Oddly, the speed that something is going doesn’t really affect how deeply it digs into the ground. Isaac Newton came up with a very clever idea for estimating how deeply projectiles will go in their targets before stopping. It turns out that no matter how fast a projectile is going, if it hits something that’s about the same density, it will only go about one body-length in.
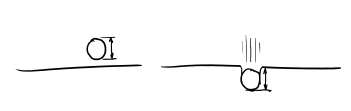
a ball falls on the ground and then falls further into the ground but not too much further
However, it will make quite a splash. The 72-kilometer-per-second diamond sphere blasts out a crater over two kilometers across, with an energy release comparable to that of the biggest fusion bombs.
Here’s where things get weird.
3,000 kilometers per second = 0.01c:
This would be pretty bad. The thing that makes this a little unpredictable is the fact that at speeds in the range of hundreds of kilometers per second, the air begins to undergo nuclear fusion (Google that paper title to find the full text). This, combined with plain old plasma heating, may manage to eat apart the diamond sphere completely before it reaches the ground.
But it doesn’t do the ground much good. The sphere doesn’t spread out enough to make a difference, and it still hits the ground in roughly one spot. The blast releases a thousand times more energy than the largest nuclear weapon, devastating whatever region it came down over. It gouges out a massive crater—though not the biggest one Earth has ever seen.
there's a hole in south america
0.99c:
This is where relativity kicks in.
At these speeds, the bonds holding the sphere together are completely irrelevant. It’s just a collection of carbon atoms moving so fast that Lorentz contraction flattens the whole thing into a pancake (although we wouldn’t be able to see that visually). The SRIM particle physics simulation tool can help answer some questions about what happens when it hits.
The carbon atoms in the ball carry about 70 GeV of energy each. They’re actually moving too fast to fuse directly with the air—they just pass through it completely. The air molecules punch three meters into the face of the ball before coming to a rest inside it, and it arrives at the ground with a bunch more matter in it than it started with. It’s also expanding rapidly.
When it hits the surface, it disintegrates completely, digging downward and outward, carving a cone-shaped path down through the bedrock. The impact depth equation no longer applies, since the atoms are literally passing through each other.
The energy cracks a hole in the crust and blows open a crater so big you can see the molten mantle. This delivers the energy of 50 dinosaur-killing Chicxulub impacts—enough to cause a mass extinction, if not end life completely.

you did this, aidan
I’ve always thought that one of the the great things about physics is that you can add more digits to any number and see what happens and nobody can stop you.
0.9999999c:
At this speed, every carbon molecule carries 25 TeV of energy, comparable to particles in the beam of the Large Hadron Collider. A little faster, and we might spot Higgs bosons in the impact debris.
As it stands, the whole thing hits the planet with about the kinetic energy of the orbiting Moon. It’s enough to punch a gaping hole in the mantle and shake up the surface across the whole planet, turning it molten. This probably ends all life on and around Earth.
Oops, cat stepped on my keyboard again and I added a bunch more 9s.
0.9999999999999999999999951c
The fastest object (with mass) in recorded history might be the Oh-My-God particle (no relation to the God particle), a proton from space that plowed into the atmosphere over Utah in 1991. It was moving at 99.99999999999999999999951% of the speed of light, which meant it packed the kinetic energy of a baseball—in a single proton. The cascade of particles it blasted apart dwarfed anything the LHC could produce.
Nobody knows how it got to be moving so fast. Particles moving that fast hit the Earth a handful of times a year. They seem to come from the general direction of exploding galaxies, but what happened to to make them leave in such a hurry—and why they haven’t slowed down more before they got here—is something of a mystery.
Let’s give Aidan’s diamond meteor the speed of the Oh My God particle.
These speeds are so high that my copy of SRIM flatly refuses to simulate them. However, we can get some idea from looking at how cosmic rays cascade through rock.
The diamond sweeps out a column of atmosphere without seeming to notice and disappears into the crust. A cloud of expanding plasma and radiation grows around the entry point as the energy ripples outward through the body of the planet. Forty milliseconds later the entire far side expands outward in an incandescent cloud.
The diamond meteor, and the cascade of particles it created as it collided with the crust, is spread out throughout the body of our planet. The superheated planet glows brighter than the sun.
The momentum would be enough to knock the Earth into a different orbit—but the Earth is no more. The energy deposited is ten thousand times greater than the planet’s gravitational binding energy, and the planet is blown into an expanding cloud of plasma, with a particularly energetic streamer extending away from the far side of the impact site, out into space.
The Sun hiccups and flares as it absorbs waves of dust. The surfaces of Mars and Venus are scoured clean by the waves of incredibly high-energy plasma.
an alien comment creates a cavalcade of theological and linguistic conundrums
And in the distant future, an alien astronomer on a world hundreds of light-years from Earth frowns at a beeping detector, and wonders what violent event would make a particle move so fast.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
Is it possible to build a jetpack using downward firing machine guns?
—Rob B
I was sort of surprised to find that the answer was yes! But to really do it right, you’ll want to talk to the Russians.
The principle here is pretty simple. If you fire a bullet forward, the recoil pushes you back. So if you fire downward, the recoil should push you up.
The first question we have to answer is “can a gun even lift its own weight?” If a machine gun weighs ten pounds but only produces eight pounds of recoil when firing, it won’t be able to lift itself off the ground, let alone lift itself plus a person.
In the engineering world, the ratio between a craft’s thrust and the weight is called, appropriately, thrust-to-weight ratio. If it’s less than 1, the vehicle can’t lift off. The Saturn V had a takeoff thrust-to-weight ratio of about 1.5.
Despite growing up in the South, I'm not really a firearms expert, so to help answer this question, I got in touch with an acquaintence in Texas. (Judging by the amount of ammunition they had lying around their house ready to measure and weigh for me, Texas has apparently become some kind of Mad Max-esque post-apocalyptic war zone.)
a Saturn 0x005 and an AK-0x002F
As it turns out, the AK-47 has a thrust-to-weight ratio of around two. This means if you stood it on end and somehow taped down the trigger (Note: Please, PLEASE do not try this at home) it would rise into the air while firing.
This isn’t true of all machine guns. The M60, for example, probably can’t produce enough recoil to lift itself off the ground.
The amount of thrust created by a rocket (or firing machine gun) depends on (1) how much mass it’s throwing out behind it, and (2) how fast it’s throwing it. Thrust is the product of these two amounts:

If an AK-47 fires ten 8g bullets per second at 715 meters per second, its thrust is:

Since the AK-47 weighs only 10.5 pounds when loaded, it will be able to take off and accelerate upward.
In practice, the actual thrust turns out to be up to around 30% higher. The reason for this is that the gun isn’t just spitting out bullets—it’s also spitting out hot gas and explosive debris. The amount of extra force this adds varies by gun and cartridge.
The overall efficiency also depends on whether you eject the shell casings out of the vehicle or carry them with you. I asked my Texan acquaintences if they could weigh some shell casings for my calculations, but for a while they couldn't find a scale anywhere in the house. I helpfully suggested that given the size of their arsenal, really they just need to find someone else who owned a scale. (Ideally someone with less ammo.)
So what does all this mean for our jetpack?
Well, the AK-47 can take off, but it clearly doesn’t have the thrust to spare to lift anything weighing much more than a squirrel.
if you see this squirrel trying to get into your bird feeder you should probably just let it
We can try multiple guns. If you fire two guns at the ground, it creates twice the thrust. If each gun can lift five pounds more than their own weight, two can lift ten.
At this point, it’s clear where we’re headed:
you will not go to space today
If we add enough rifles, the weight of the passenger becomes irrelevant. it’s spread over so many of them that they don’t notice. As the number of rifles increases, since it’s effectively many individual rifles flying in parallel, the craft’s thrust-to-weight ratio approaches that of a single, unburdened rifle:
a graph whose axes are 'thrust-to-weight ratio' and 'number of AK-47s' (log scale)
But there’s a problem: Ammunition.
An AK-47 magazine holds 30 rounds. At ten per second, we’ll get a measly three seconds of acceleration. We can improve this with a larger magazine—but only up to a point.
It turns out there’s no advantage to carrying more than about 250 rounds of ammunition. The reason for this is a fundamental and central problem in rocket science: Fuel makes you heavier.
Each bullet weighs 8 grams, and the cartridge (the “whole bullet”) weighs over 16 grams. If we add more than about 250 rounds, the AK-47 is too heavy to take off.
This suggests our optimal craft comprises a large number of AK-47s (a minimum of 25 but ideally at least 300) carrying 250 rounds of ammunition each. The largest versions of this craft could accelerate upward to vertical speeds approaching 100 meters per second, climbing over half a kilometer into the air. (If you want to work through the math on that in more detail, there’s a good primer here.)
So we’ve answered Rob’s question. With enough machine guns, you could fly.
But our 500xAK-47 rig is clearly not a practical jetpack. Can we do better?
My Texas friends suggested a series of machine guns, and I ran the numbers on each one. Some did pretty well; the MG-42, a heavier machine gun, had a marginally higher thrust-to-weight ratio than the AK-47.
Then we went bigger.
The GAU-8 Avenger fires up to sixty one-pound bullets a second. It produces almost five tons of recoil force, which is crazy considering that it’s mounted in a type of plane (the A-10 “Warthog”) whose two engines produce only four tons of thrust each. If you put two of them in one aircraft, and fired both guns forward while opening up the throttle, the guns would win and you’d accelerate backward.
To put it another way: If I mounted a GAU-8 on my car, put the car in neutral, and started firing backward from a standstill, I would be breaking the interstate speed limit in less than three seconds.
actually, what i'm confused about is 'how'.
As good as this gun would be as a rocket pack engine, the Russians built one that would work even better. The Gryazev-Shipunov GSh-6-30 weighs half as much as the GAU-8 and has an even higher fire rate. Its thrust-to-weight ratio approaches 40, which means if you pointed one at the ground and fired, not only would it take off in a rapidly expanding spray of deadly metal fragments, but you would experience 40 gees of acceleration.
This is way too much. In fact, even when it was firmly mounted in an aircraft, the acceleration was a problem:
[T]he recoil … still had a tendency to inflict damage on the aircraft. The rate of fire was reduced to 4,000 rounds a minute but it didn't help much. Landing lights almost always broke after firing … Firing more than about 30 rounds in a burst was asking for trouble from overheating …
But if you somehow braced the human rider, made the craft strong enough to survive the acceleration, wrapped it in an aerodynamic shell, and made sure it was adequately cooled ...
a pilot leaves an area very quickly by shooting it a lot and then flies over a mountain.
… with a GSH-6-30, you could jump mountains.
i remember wondering if i should wait for you on ometepe or leave things happy as we had left them, happy memories, but i waited and i can still feel your presence filling my chest when you got there
If you carry a penny in your coin tray, how long would it take for that penny to cost you more than a cent in extra gas?
—Leto Atreides
At current prices, 140,000 miles, close to the average car’s lifetime mileage:
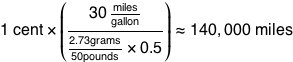
That means that as long as you go through pennies faster than you go through cars, you’re coming out ahead. (The equation assumes, for a 30 mpg car, 50 lbs of cargo means a 0.5% hit in fuel economy.)
But gas money isn’t the only cost attached to a penny. Let’s consider some of the others.
Suppose you found it on the ground on the way to your car. How much did it cost you to pick it up in the first place?
How much is your time worth? This obviously depends on a lot of things and varies from time to time and person to person. But for a broad estimate, I sometimes use a ballpark value of $10/hour—which is somewhere between the US minimum wage and the average wage—but you can adjust up or down to fit your preference.
If your time is worth $10 an hour, a penny is worth 3.6 seconds. If spotting and picking up a penny takes you more than 3.6 seconds, it’s a loss.

actually, wait, is that a wheat penny?
Of course, picking it up isn’t the only time cost. Having a penny in your pocket makes it harder to find other things there, so you might spend more time looking for stuff in the future.
And then there’s the future time spent dealing with the penny. You may spend time figuring out if it helps you make change, putting it in a roll, donating them, or doing countless other hard-to-predict things. (You may argue that dropping them in a donation jar is noble enough that it makes picking them up worthwhile. That may be true; it’s what I do with pennies. But this isn’t an argument against donating money—it’s just an argument that picking up pennies may not be an efficient way to use your time to acquire money to donate.)
There’s another cost (and benefit) to picking up a penny—the calories burned. When you crouch to pick up a penny, you expend energy. A 70-kilogram person who lowers their center of mass by half a meter will burn about half a calorie of energy standing back up:
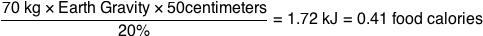
(The “20%” represents the overall energy efficiency of the squatting process, which I based on the efficiency of stair climbing.)
All else being equal, to replenish those 0.41 extra calories, you’ll need to eat 0.41 calories worth of extra food. And food costs money.
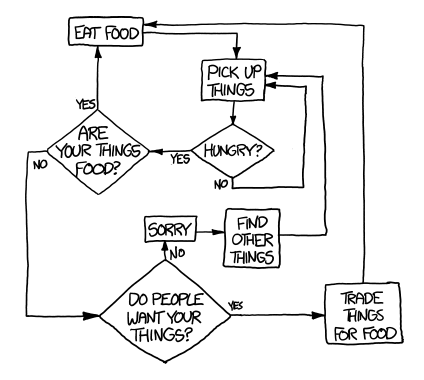
a chart which can replace two semesters of economics and three of agronomy
Donuts provide 836 calories per dollar, or 8.3 calories per penny—plenty to supply the 0.41 needed to pick one up. On the other hand, if you get your energy from expensive fresh strawberries, you might only get 20 calories per dollar—meaning that picking up that penny costs you 2 cents in extra strawberry. (In dollars per calorie, the cheapest energy sources in the supermarket are refined sugar, oil, and shortening).
But on the other hand, burning calories is exercise, which is good for you. Crouching to pick up that penny is equivalent to two or three seconds on an exercise machine. What’s that worth?

picking up a penny is a potentially exhausting activity
Well, one study suggests that 15 minutes of moderate exercise per day adds three years to your life expectancy (with smaller improvements in mortality rate for progressively more daily exercise). It’s a tremendous oversimplification, but a crude back-of-the-envelope estimate suggests each calorie burned adds something like 30 seconds to your life—or 12 seconds per penny.
But wait—if it only takes a couple seconds to pick up a penny, but it pays back 12 seconds, then you could game the system by repeatedly dropping a penny and picking it back up ...
a lifespan is boosted by repeatedly picking up a penny
… which is just another way of saying that exercise is a good idea.

a realization occurs in the brain
One final thought:
This article is about 770 words long. If you read at 250 words per minute, then add in another couple minutes for the drawings and equations, then reading this article has eaten up 300 seconds of your time. At $10/hour, that’s 83 cents.
Which means that by reading this article, you’ve quite possibly erased the gains from all the pennies you’ll pick up in your entire life and any gains in fuel economy due to keeping a clean change cup.
a chart shows how the text around it has ruined everything for you
You’re welcome.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
In today’s article, I give shorter answers to several reader questions. (Previous installment here.)
If my printer could literally print out money, would it have that big an effect on the world?
—Derek O'Brien
You can fit four bills on an 8.5”x11” sheet of paper:
these notes are legal tender for all debts, public, private, legal, ancestral, emotional, and wookiee life.
If your printer can manage one page (front and back) of full-color high-quality printing per minute, that’s $200 million dollars a year.

a counterfeiter uses the song 'seasons of love' to figure out his annual income
This is enough to make you very rich, but not enough to put any kind of dent in the world economy. Since there are 7.8 billion \$100 bills in circulation, and the lifetime of a \$100 bill is about 90 months, that means there are about a billion produced each year. Your extra two million bills a year would barely be enough to notice.
What would happen if you exploded a nuclear bomb in the eye of a hurricane? Would the storm cell be immediately vaporized?
—Rupert Bainbridge (and hundreds of others)
This question gets submitted a lot.
It turns out the National Oceanic and Atmospheric Administration—the agency which runs the National Hurricane Center—gets it a lot, too. In fact, they’re asked about it so often that they’ve published a response.
I recommend you read the whole thing, but I think the last sentence of the first paragraph says it all:
“Needless to say, this is not a good idea.”
It makes me happy that an arm of the US government has, in some official capacity, issued an opinion on the subject of firing nuclear missiles into hurricanes.
If everyone put little turbine generators on the downspouts of their houses and businesses, how much power would we generate? Would we ever generate enough power to offset the cost of the generators?
—Damien
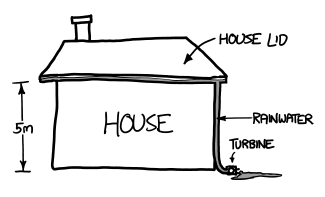
a house uses rain that falls on its lid to run a turbine
A house in a very rainy place, like the Alaska panhandle, might receive close to four meters of rain per year. Water turbines can be pretty efficient. If the house has a footprint of 1,500 square feet and gutters five meters off the ground, it would generate an average of less than a watt of power from rainfall, and the maximum electricity savings would be:
The rainiest hour on record occurred in 1947 in Holt, Missouri, where about 30 centimeters of rain fell in 42 minutes. For those 42 minutes, our hypothetical house could generate up to 800 watts of electricity, which might be enough to power everything inside it. For the rest of the year, it wouldn’t come close.
If the generator rig cost $100, residents of the rainiest place in the US—Ketchikan, Alaska—could potentially offset the cost in under a century.
Using only pronounceable letter combinations, how long would names have to be to give each star in the universe a unique one word name?
—Seamus Johnson
There are about 300,000,000,000,000,000,000,000 stars in the universe. If you make a word pronounceable by alternating vowels and consonants (there are better ways to make pronounceable words, but this will do for an approximation), then every pair of letters you add lets you name 105 times as many stars (21 consonants times 5 vowels). 105 possibilities per two characters is about the same information density that numbers have, which suggests the name will end up being about as long as the total number of stars written out:
the stars are named joe biden
I like doing math that involves measuring the lengths of numbers written out on the page—which is really just a way of loosely estimating log~10~x. It works, but it feels so wrong.
I bike to class sometimes. It's annoying biking in the wintertime, because it's so cold. How fast would I have to bike for my skin to warm up the way a spacecraft heats up during reentry?
—David Nai
Reentering spacecraft heat up because they’re compressing the air in front of them (not, as is commonly believed, because of air friction).
According to this calculator, to increase the temperature of the air layer in front of your body by twenty degrees Celsius (enough to go from freezing to room temperature), you would need to be biking at 200 m/s.
The fastest human-powered vehicles at sea levels are recumbent bicycles enclosed in streamlined aerodynamic shells. These vehicles have an upper speed limit near 40 m/s. This is the speed at which the human can just barely produce enough thrust to balance the drag force from the air.
Since drag increases with the square of the speed, this limit would be pretty hard to push any further. Biking at 200 m/s would require at least 25 times the power output needed to go 40 m/s.
At those speeds, you don’t really have to worry about the heating from the air—a quick back-of-the-envelope calculation suggests that if your body were doing that much work, your core temperature would reach fatal levels in a matter of seconds.
How much physical space does the internet take up?
—Max L
There are a lot of ways to estimate the amount of information stored on the internet, but we can put an interesting upper bound on the number just by looking at how much storage space we (as a species) have purchased.
The storage industry produces in the neighborhood of 650 million hard drives per year. If most of them are 3.5” drives, then that’s eight liters (two gallons) of hard drive per second.
This means the last few years of hard drive production—which, thanks to increasing size, represent a large chunk of global storage capacity—would just about fill an oil tanker. So, by that measure, the internet is smaller than an oil tanker.
What if you strapped C4 to a boomerang? Could this be an effective weapon, or would it be as stupid as it sounds?
—Chad Macziewski
it's the second one
Aerodynamics aside, I’m curious what tactical advantage you’re expecting to gain by having the high explosive fly back at you if it misses the target.
again we cuddled, we hugged, we laughed, we danced, and we talked through the nights, feeding on watermelon and bread
How many model rocket engines would it take to launch a real rocket into space?
—Greg Schock, PA
About 65,000, give or take a few.
You’d have to arrange them like this:
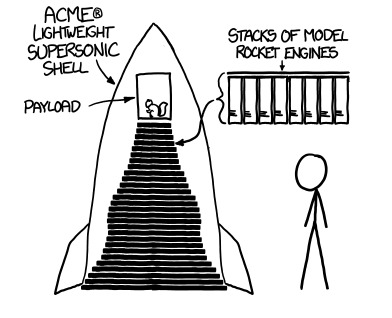
a stack of model rocket engines with a rocket shell around them
The rocket would weigh about as much as a tow truck. There wouldn’t be room for anything except the engines, aerodynamic shell, and minimal staging equipment.
Each rocket motor would burn for about three seconds. The layer cake arrangement means that every three seconds, the bottom layer of spent rockets would detaches and the next stage would kick in. It would go through between 25 and 30 of these stages, burning for a total of a minute and a half, after which it would coast upward and just barely brush the edge of space.
(For this design, I’m assuming something akin to Estes E9-4 engines, which are on the large end of the common model rocket engines. There are larger ones—the classes go all the way up to O and beyond—but at a certain point, they stop being model rocket engines, and just become rocket engines.)
A 30-stage rocket is, to put it lightly, an engineering nightmare. This design assumes the non-engine portion of the vehicle is limited to the weight of a person (60 kg). In effect, the spaceship would be a solid block of rocket engines. They’d need to be insulated from each other so the upper stages didn’t ignite prematurely, and the staging and aerodynamics would both be a challenge.
The stack of engines narrows as you go from bottom to top. By the time the top stages are firing, the rocket will have shed most of its mass, so it won’t need as much thrust to get the same acceleration.
The reason the engine stack bulges in the middle is so that the acceleration profile will look like this:
a curve showing acceleration that starts small and then gets large about halfway through
Rockets work best when their thrust is several times greater than the force of gravity. But you don’t want to accelerate too quickly while you’re low down. Air drag increases with the square of your speed, and if you accelerate too quickly, you’ll find yourself wasting all your fuel just to maintain your speed. You want to accelerate slowly at first, then ramp it up as the air starts getting thinner.
a rocket goes from not space to space and back to not space. then it lands a lot.
Now, as you may have noticed, this rocket will get you into space (for a few seconds, at least), but not orbit. Can you use model rocket engines to dock with the ISS?
No.
Taking into account atmospheric drag, to get into space, you need a rocket capable of accelerating (in a vacuum) to about 2 kilometers per second. To get to orbit, you need a rocket capable of accelerating to about 10 kilometers per second.
If you try to produce an orbital rocket using the same design math we used for the suborbital rocket, it spits out a description of a pancake-shaped mountain of model rocket engines over a mile wide. It would taper to a 10-meter-high spire in the center and would weigh about as much as the Great Pyramid.

THIS is your ship? ... we're gonna need a bigger shark.
Not only would this vehicle never get out of the atmosphere, it would probably not stand up under its own weight.
Frankly, the word “vehicle” is a bit misleading. Essentially, what you’ve created is an unstable pile of gunpowder the size of Central Park. If it went up in flames—which it would—it would break the record for the largest manmade non-nuclear explosion in history. (Interestingly, the current holder of that dubious record is also a rocket that exploded during launch.)
The bottom line is that it would be very difficult, but perhaps not impossible, to launch something up to the edge of space using model rocket engines. However, if you try to build a ship capable of getting to orbit, you will not go to space today.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
The story of the three wise men got me wondering: What if you did walk towards a star at a fixed speed? What path would you trace on the Earth? Does it converge to a fixed cycle?
—N. Murdoch
If the wise men leave Jerusalem and walk toward the star Sirius, day and night, even when it’s below the horizon, this is the path they follow over the surface:
several star-struck sages spiral southward
If we allow a little theological confusion and assume the wise men can walk on water, they’ll eventually wind up going in an endless circle, 30 kilometers in diameter, around the South Pole.
But let’s be a little more realistic; the wise men are hardly going to walk toward the star while it’s behind the Earth. Let’s assume that they only walk toward the star when it’s in the sky and the Sun has set.
In that case, their path actually takes them through Bethlehem:

the wise men attack jerusalem with half a pincer maneuver
If they don’t stop there, after a few years, they wind up orbiting Botswana:
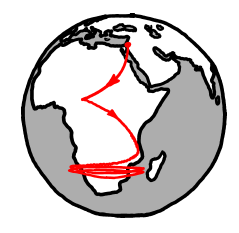
a child, a child, sweating in the heat / we will bring him netting and deet
These paths are calculated using, among other things, PyEphem, which provides tools for determining the historical positions of astronomical objects.
It’s tricky to figure out exactly what the wise men would have been following. There aren’t very many good astronomical candidates for the Star of Bethlehem (Chinese records don’t show a supernova at the right time, and none of the other obvious candidates check out) and, furthermore, there’s a lot of historical and theological debate over Jesus’s date of birth (“4 BC” seems to be the closest thing to a historical consensus date). These charts are all calculated for a somewhat arbitrary departure date from Jerusalem of December 25th, 1 AD; different departure days would lead to different paths, but the overall picture would be the same.
What if the wise men followed a planet?
Planets move against the background of stars, so the paths they produce are more complex. Here’s where the Wise Men would’ve gone if they followed Venus:
the wise men lose interest in the child and vacation in tripoli and the red sea instead
And here’s their path for Mars:
the three wise men look for the baby jesus atop mt. everest, which is a logical place to look if you assume he's descending from heaven and stopping at the first land he reaches
If the three wise men had a hovercar that could move at highway speed over land and water (it’s in the gnostic gospels somewhere) and decided to follow Venus, they’d take a particularly weird path:
the three wise men and their magical hovercar, starring donald glover, kal penn, andy samberg, and neil patrick harris as the hovercar
At one point, they wind up near the North Pole in October. There, the Sun and Venus spend months near the horizon, rising and setting, nudging the Magi into a month-long spiral around the pole, a chaotic strange Magi attractor around the North Pole which some argue provides the theological foundation for the story of Santa Claus [citation needed].
Sadly, the three wise men probably weren’t following Venus. It’s one of the most familiar objects in the night sky, and as the late Sir Patrick Moore observed, if the wise men mistook it for a new star, they couldn’t have been very wise.
But maybe they’re wiser than Sir Patrick gives them credit for. After all, if you pick a random star in the sky, point at the horizon, and predict that there’s a baby about to be born in that direction, statistics—and birth rates—are on your side.
and the tiger offered the bear to look for a cool place
Every now and then we have to insert a leap second because the Earth’s rotation is slowing down. Could we speed up Earth’s rotation, so that we do not need Leap Seconds?
—Anton (Berlin, Germany)
The Earth’s spin is slowing down. This is annoying.
One reason that it’s annoying is that it makes time standards more difficult. We already have way too many time standards, including:
This leads to all kinds of little headaches, particularly for programmers. For example, the clock in your smartphone’s GPS is 16 seconds out of sync with the phone’s system clock. This is because the system clock uses Coordinated Universal Time (which has leap seconds), but GPS time doesn’t. They were in sync in January of 1980 and probably never will be again.
Half a billion years ago (when the Earth was 4 billion years old, instead of 4.5), each day was 22 hours long instead of 24. The day has gotten longer because of tidal forces from the Moon.
Loosely speaking, here’s how tidal drag works: The Moon’s tides raise bulges in the Earth, but the Earth’s rotation moves those bulges out of line with the Moon. The Moon’s gravity tries to tug the bulges back into line, which exerts a twisting force on the Earth, slowing it down:
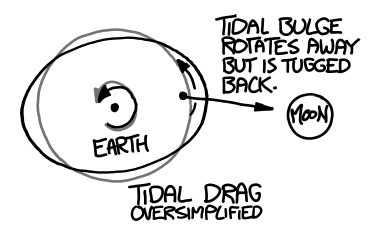
a picture explaining tidal drag that is wrong in almost every specific way but right in general
Strangely, the Earth is actually not slowing down as much as you’d expect from tidal drag. The biggest reason for the discrepancy is that during the last ice age, the continents were pushed down by the weight of the glaciers, and they’re still springing back into place. This has the effect of shifting mass toward the poles, closer to the axis of rotation:
the earth springs back into shape
This makes us spin faster—or, at least, keeps us from slowing down as quickly.
At the moment, each day is about 0.8 milliseconds longer than the 86,400 seconds it needs to be to avoid adding leap seconds.
a graph documenting the war between timekeepers and time
This difference fluctuates over time based on weather and other effects (it’s actually shortened a bit since the early 1990s), although in the long run, it will definitely get larger as the Earth slows.
If we wanted to get rid of leap seconds, we’d need to keep the Earth spinning at a more constant rate. This means speeding up the Earth and shortening each day by about 0.8 milliseconds.
This is a tough problem. Here are a few things that won’t work:
Spinning counterclockwise in a chair. It temporarily alters the Earth’s rate of rotation, but not enough to matter.
Putting rocket engines on the Equator. This won’t work because the exhaust would go into the atmosphere, which transmits the force back to the ground as wind drag—it’d be like making a bike go forward by pushing on the handlebars. If the engines were somehow mounted above the atmosphere, they’d be able to slow the Earth, but not by enough to accomplish our goal.
Triggering big earthquakes. This can alter the length of the day, but even those aren’t big enough to make a difference.
In the end, there’s only one solution: Hitting the Earth with asteroids.
Given enough time, we could send a spaceship (captained by an anti-Bruce Willis) to perform repeated flybys of a comet. Over time, the gravitational perturbation could steer the comet into a collision course with Earth. By hitting the Earth at the right angle, we would give it a push:
a meteor hits the earth to fix the problems
Even if the comet burns up in the atmosphere, its momentum is transmitted to the surface by wind drag (taking a matter of days). It takes about a decade for the core to sync up with the crust, so we’d have to plan the impact schedule carefully to avoid overshooting.
Here’s the bad news: To get enough spin, we have to hit the Earth with on the order of a billion liters of rock per second (several times the volumetric discharge rate of the Amazon). This adds up to about one six-mile dinosaur-killing asteroid every couple days. Humanity—and life—wouldn’t survive the bombardment long.
What about a steady stream of smaller asteroids?
the bullet
If asteroid B-612 in The Little Prince is four meters across and made of rock, we’d need an average of around fifty thousand of them to enter the atmosphere each second to keep up the pressure.
is programming convenience worth *this*? is it, anton?
Unfortunately, the steady high-altitude meteor shower would deliver just as much energy to the atmosphere that daily giant impacts would, and the eventual death toll would be the same: Seven billion humans, plus four billion Little Princes per day.
But at least we could stop worrying about leap seconds.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
If one randomly chosen extra person were to die each second somewhere on Earth, what impact would it have on the world population?
—Guy Petzall
Every second, 1.8 humans die and 4.2 humans are born. Under Mr. Petzall’s plan, the number of deaths would increase to 2.8.
This randomized culling would obviously be a big deal—it would be responsible for over a third of all deaths—but, at least for a while, our population would continue to grow.
At one death per second, any given person currently has a 0.464% chance of being chosen each year. Put another way, the scenario would result in 4.64 deaths per 1,000 people (or 464 per 100,000).
a thousand people, 19 of whom are recently born and 12 of whom have recently died
There are about twenty countries with death rates below 4.64 per 1,000. It’s an odd bunch, including the Dominican Republic, Brunei, Singapore, Saudi Arabia, Kuwait, the Maldives, and Paraguay. These are the countries where Guy’s program would be responsible for the majority of all deaths.
The death rate in all of these countries is going to go up. It has to, because of math. It seems intuitively obvious that death rates below 10 per 1,000 are unsustainable. If fewer than one person out of every hundred dies each year (and enough are born to sustain the population) then the average person must have to wait over a hundred years to die—which is clearly not compatible with our current lifespans.
In those countries with low single-digit death rates, the rates are guaranteed to rise in the future. This includes the United States, whose death rate is 8.40 per 1,000—a number which will go up substantially as the Baby Boomers age.
A rate of one death per second isn’t enough to reverse population growth at present, but it would have been until recently. In 1950, the world’s population was only 2.52 billion. One death per second would mean 12.5 annual deaths per 1,000 people, almost triple the number in 2013. At the start of the early 20th century, this would have been enough to reverse population growth, and within a handful of decades—as population levels off—it will be again. Of course, if people die faster, this in turn has an effect on birth rates—as people change their behavior in response to the change in mortality—so the actual result would be more complicated.
a graph showing that death from traditional causes would dominate in infants and retirees, while death from guy petzall's scenario would dominate the in-between group
In the United States, Guy Petzall would be the leading cause of death for females between the ages of 1 and 55 and for males between the ages of 1 and 48. Currently, about 96% of infants survive to age 40, but in Guy’s scenario, only 80% would.
When would these deaths happen?
Given the numbers of aircraft in the air at any given time, it’s certain that some pilots would die while flying. This wouldn’t be a disaster, though, since large commercial airliners have multiple crew members who can take over.
Cars would be a different story. Since about 10 million Americans are driving at any given time, 127 will die behind the wheel each day (plus a smaller but still significant number of passengers, pedestrians, and other drivers). Interestingly, this is only a little larger than the number of Americans who die in car accidents every day already. (This number has been declining, as a percentage of population, since the 1960s, and as a percentage of miles traveled since at at least the 1920s.)
About 50 million outpatient surgery procedures are performed each year. If they’re primarily performed by one surgeon and each last an average of half an hour, then about 13 surgeons per year will unexpectedly die mid-surgery (as will 13 extra patients). This is a scary thought. But to put it in perspective, that’s about the number of surgeons who will operate on the wrong body part or wrong patient every two days. It’s not that the scenario isn’t scary. It’s just that reality is far more terrifying.
Lastly, what about our leaders?
Members of Congress die in office at a rate of two or three per year, or about five per Congress. This used to be much higher, as explained in this strangely florid paper. 29 members of Congress died during 1939 and 1940, the two years the 76th Congress was in session. In Guy’s scenario, the current rate would double, leading to a loss of 10 per Congress. This would certainly be tragic, but it would be no higher than the levels seen as recently as the 1960s.
All in all, the losses would be dramatic, but not devastating to our species as a whole. And really, in the end, the global death rate is 100%—everyone dies.

everyone dies eventually, so to save money let's all go in on a single gravestone together
… or do they? Strictly speaking, the observed death rate for the human condition is something like 93%—that is, around 93% of all humans have died. This means the death rate among humans who were not members of The Beatles is significantly higher than the 50% death rate among humans who were.
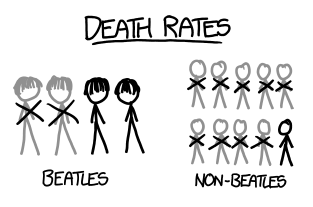
beatles avoid the grim reaper more skillfully than non-beatles
I expect this significant[dubious–discuss] fact[citation needed] will pave the way[citation needed] for a great deal[dubious–discuss] of important[citation needed][dubious–discuss] research.
off we went on this geatest bus ride ever, still hugging and never letting go
From what height would you need to drop a steak for it to be cooked when it hit the ground?
—Alex Lahey
I hope you like your steaks Pittsburgh Rare. And you may need to defrost it after you pick it up.
Things get really hot when they come back from space. This isn’t because of air friction, strictly speaking—it’s because of air compression. The air can’t move out of the way fast enough, and gets squished in front of the spaceship/meteor/steak. Compressing air heats it up. As a rule of thumb, you start to notice compressive heating above about Mach 2 (which is why the Concorde had heat-resistant material on the leading edge of its wings).
A few months ago, skydiver Felix Baumgartner jumped from 39 kilometers, and hit Mach 1 around 30 kilometers. This was enough to heat the air by a few degrees, but the air was so far below freezing that it didn’t make a difference. (Early in his jump, it was about minus 40 degrees, which is that magical point where you don’t have to clarify whether you mean Fahrenheit or Celsius—it’s the same in both.)
As far as I know, this steak question originally came up in a lengthy 4chan thread, which quickly disintegrated into poorly-informed physics tirades intermixed with homophobic slurs. There was no clear conclusion.
To try to get a better answer, I decided to run a series of simulations of a steak falling from various heights.
This involved a lot of research.
I used Mathematica models of atmospheric density to generate a set of descent profiles for the plummeting steak. For a nice tutorial on how to do this, see the Wolfram Blog’s analysis of Felix Baumgartner’s jump.
An 8 oz. steak is about the size and shape of a hockey puck, so I based my steak’s drag coefficients on those given on page 74 of The Physics of Hockey (which author Alain Haché actually measured personally using some lab equipment). A steak isn’t a hockey puck, but the precise drag coefficient turned out not to make a big difference in the result.
I used a handy NASA compressive heating calculator to determine the temperature of the shock layer in front of the steak.
Since this blog tends to wind up looking at unusual objects in extreme physical circumstances, often the only relevant research I can find is US military studies from the Cold War era. (Apparently, the US government was shoveling tons of money at anything even loosely related to weapons research.) To get an idea of how the air would heat the steak, I looked at research papers on the heating of ICBM nose cones as they reenter the atmosphere. Two of the most useful were Predictions of Aerodynamic Heating on Tactical Missile Domes and Calculation of Reentry-Vehicle Temperature History.
Lastly, I had to figure out exactly how quickly heat spreads through a steak. I started by looking at some papers from industrial food production which simulated heat flow through various pieces of meat. It took me a while to realize there was a much easier way to learn what combinations of time and temperature will effectively heat the various layers of a steak: Check a cookbook.
Jeff Potter’s excellent book Cooking for Geeks provides a great introduction to the science of cooking meat, and explains what ranges of heat produce what effects in steak and why. Cook’s The Science of Good Cooking was also helpful.
Putting it all together, I found that the steak will accelerate quickly until it reaches about an altitude of about 30-50 kilometers, at which point the air gets thick enough to start slowing it back down.
The falling steak’s speed drops steadily as the air gets thicker. No matter how fast it’s going when it reaches the lower layers of the atmosphere, it quickly slows down to terminal velocity. It always takes six or seven minutes to drop from 25 kilometers to the ground.
For much of those 25 kilometers, the air temperature is below freezing—which means the steak will spend six or seven minutes subjected to a relentless blast of subzero, hurricane-force winds. Even if it is cooked by the fall, you’ll probably have to defrost it when it lands.
When the steak does finally hit the ground, no matter the initial height, it will be traveling at about 30 meters per second. To get an idea of what this means, imagine a steak flung at the ground by a major-league pitcher. If the steak is even partially frozen, it could easily shatter. However, if it lands in the water, mud, or leaves, it will probably be fine. (Not clean, but intact.)
A steak dropped from 39 kilometers will, unlike Felix, probably not break the sound barrier. It also won’t be appreciably heated. This makes sense—after all, Felix’s suit wasn’t scorched when he landed.

a graph of an 8 oz. steak's downward velocity as a function of altitude
Steaks can probably survive breaking the sound barrier. In addition to Felix, pilots have ejected at supersonic speeds and lived to tell about it.
To break the sound barrier, you’ll need to drop the steak from about 50 kilometers. But this isn’t enough to cook it.
We need to go higher.
If dropped from 70 kilometers, the steak will go fast enough to be briefly blasted by 350°F air. Unfortunately, this blast of thin, wispy air barely lasts a minute—and anyone with some basic kitchen experience can tell you that a steak placed in the oven at 350 for 60 seconds isn’t going to be cooked.
From 100 kilometers—the formally defined edge of space—the picture’s not much better. The steak spends a minute and a half over Mach 2, and the outer surface will likely be singed, but the heat is too quickly replaced by the icy stratospheric blast for it to actually be cooked.
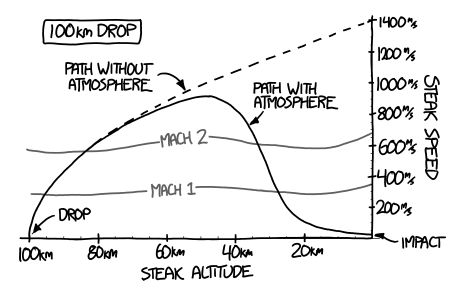
a graph of chuck yeager eating breakfast
At supersonic and hypersonic speeds, a shockwave forms around the steak which helps protect it from the faster and faster winds. The exact characteristics of this shock front—and thus the mechanical stress on the steak—depend on how an uncooked 8 oz. filet tumbles at hypersonic speeds. I searched the literature, but was unable to find anything to help me estimate this.
For the sake of this simulation, I assume that at lower speeds some type of vortex shedding creates a flipping tumble, while at hypersonic speeds it’s squished into a semi-stable spheroid shape. However, this is little more than a wild guess. If anyone puts a steak in a hypersonic wind tunnel to get better data on this, please, send me the video.
If you drop the steak from 250 kilometers, things start to heat up. 250 kilometers puts us in the range of low earth orbit. However, the steak, since it’s dropped from a standstill, isn’t moving nearly as fast as an object re-entering from orbit.
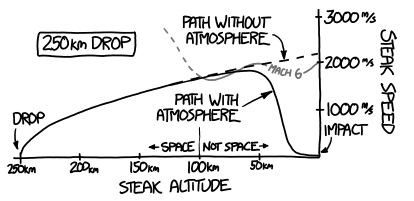
a hypersonic steak breaks mach 6 while elsewhere a jam band produces an instrumental album titled 'hypersonic steak 6'
The steak reaches a top speed of Mach 6, and the outer surface may even get pleasantly seared. The inside, unfortunately, is still uncooked. Unless, that is, it goes into a hypersonic tumble and explodes into chunks.
From higher altitudes, the heat starts to get really substantial. The shockwave in front of the steak reaches thousands of degrees (Fahrenheit or Celsius; it’s true in both). The problem with these levels of heat is that it burns the surface layer completely, converting it to little more than carbon. That is, it becomes charred.
Charring is a normal consequence of dropping meat in the fire. The problem with charring meat at hypersonic speeds is that the charred layer doesn’t have much structural integrity, and is blasted off by the wind—exposing a new layer to be charred. (If the heat is high enough, it will simply blast the surface layer off as it flash-cooks it. This is referred to in the ICBM papers as the “ablation zone”)
Even from those heights, the steak stilldoesn’t spend enough time in the heat to get cooked all the way through. (I know what some of you are probably thinking, and the answer is no—it doesn’t spend enough time in the Van Allen belts to be sterilized by radiation).
We can try higher and higher speeds, and we might lengthen the exposure time via dropping it at an angle, from orbit.
But if the temperature is high enough or the burn time long enough, the steak will slowly disintegrate as the outer layer is repeatedly charred and blasted off. If most of the steak makes it to the ground, the inside will still be raw.
Which is why we should drop the steak over Pittsburgh.
As the probably-apocryphal story goes, steel workers in Pittsburgh would cook steaks by slapping them on the glowing metal surfaces coming out of the foundry, searing the outside while leaving the inside raw. This is, supposedly, the origin of the term Pittsburgh Rare.
So drop your steak from a suborbital rocket, send out a collection team to recover it, brush it off, reheat it, cut away any badly charred sections, and dig in.
Just watch out for salmonella. And the Andromeda Strain.

this waiter is going to regret asking me how i'd like my steak cooked
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
What if I took a swim in a typical spent nuclear fuel pool? Would I need to dive to actually experience a fatal amount of radiation? How long could I stay safely at the surface?
—Jonathan Bastien-Filiatrault
Assuming you’re a reasonably good swimmer, you could probably survive treading water anywhere from 10 to 40 hours. At that point, you would black out from fatigue and drown. This is also true for a pool without nuclear fuel in the bottom.
Spent fuel from nuclear reactors is highly radioactive. Water is good for both radiation shielding and cooling, so fuel is stored at the bottom of pools for a couple decades until it’s inert enough to be moved into dry casks. We haven’t really agreed on where to put those dry casks yet. One of these days we should probably figure that out.
Here’s the geometry of a typical fuel storage pool:
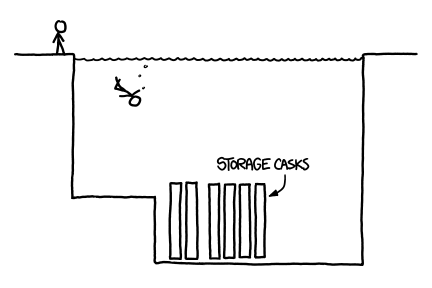
the geometry of a spent fuel pool
The heat wouldn't be a big problem. The water temperature in a fuel pool can in theory go as high as 50°C, but in practice they're generally between 25°C and 35°C—warmer than most pools but cooler than a hot tub.
For the kinds of radiation coming off spent nuclear fuel, every 7 centimeters of water cuts the amount of radiation in half.
The most highly radioactive fuel rods are those recently removed from a reactor. Based on the activity levels provided by Ontario Hydro in this report, this would be the region of danger for fresh fuel rods:

a diagram shows the parts of a spent fuel pool which you should not swim in
Swimming to the bottom, touching your elbows to a fresh fuel canister, and immediately swimming back up would probably be enough to kill you.
Yet outside the outer boundary, you could swim around as long as you wanted—the dose from the core would be less than the normal background dose you get walking around. In fact, as long as you were underwater, you would be shielded from most of that normal background dose. You may actually receive a lower dose of radiation treading water in a spent fuel pool than walking around on the street.

disclaimer: i am a cartoonist. if you follow my advice on safety around nuclear materials you probably deserve whatever happens to you.
That’s if everything goes as planned. If there’s corrosion in the spent fuel rod casings, there may be some fission products in the water. They do a pretty good job of keeping the water clean, and it wouldn’t hurt you to swim in it, but it’s radioactive enough that it wouldn’t be legal to sell it as bottled water. (Which is too bad—it’d make a hell of an energy drink).
We know spent fuel pools can be safe to swim in because they’re routinely serviced by human divers.
However, these divers have to be careful.
On August 31st, 2010, a diver was servicing the spent fuel pool at the Leibstadt nuclear reactor in Switzerland. He spotted an unidentified length of tubing on the bottom of the pool and radioed his supervisor to ask what to do. He was told to put it in his tool basket, which he did. Due to bubble noise in the pool, he didn’t hear his radiation alarm.
When the tool basket was lifted from the water, the room’s radiation alarms went off. The basket was dropped back in the water and the diver left the pool. The diver’s dosimeter badges showed that he’d received a higher-than-normal whole-body dose, and the dose in his right hand was extremely high.
The object turned out to be protective tubing from a radiation monitor in the reactor core, made highly radioactive by neutron flux. It had been accidentally sheared off while a capsule was being closed in 2006. It sank to a remote corner of the pool floor, where it sat unnoticed for four years.
The tubing was so radioactive that if he’d tucked it into a tool belt or shoulder bag, where it sat close to his body, he could’ve been killed. As it was, the water protected him, and only his hand—a body part more resistant to radiation than the delicate internal organs—received a heavy dose.
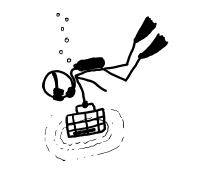
the most ominous edible arrangements basket ever
So, as far as swimming safety goes, the bottom line is that you’d probably be ok, as long as you didn’t dive to the bottom or pick up anything strange.
But just to be sure, I got in touch with a friend of mine who works at a research reactor, and asked him what he thought would happen to you if you tried to swim in their radiation containment pool.
“In our reactor?” He thought about it for a moment. “You’d die pretty quickly, before reaching the water, from gunshot wounds.”
i like you
What would happen if you tried to fly a normal Earth airplane above different Solar System bodies?
—Glen Chiacchieri
Here’s our aircraft:

We have to use an electric motor because gas engines only work near green plants. On worlds without plants, oxygen doesn’t stay in the atmosphere—it combines with other elements to form things like carbon dioxide and rust. Plants undo this by stripping the oxygen back out and pumping it into the air. Engines need oxygen in the air to run. (Also, our gasoline is MADE of ancient plants.)
The Cessna 172 Skyhawk, probably the most common plane in the world.
Here’s our pilot:
i do not want to go to space today
Here’s what happens when the aircraft is launched above the surface of the 32 largest Solar System bodies:
THIS ONE HAS NO ATMO-- WHY DO YOU KEEP-- ARGH!
In most cases, there’s no atmosphere, and the plane falls straight to the ground. (If it’s dropped from one kilometer, in a few cases, the crash will be slow enough that the pilot may survive—although the life-support equipment probably won’t.)
There are nine Solar System bodies with atmospheres thick enough to matter: Earth—obviously—Mars, Venus, the four gas giants, Saturn’s moon Titan, and the Sun. Let’s take a closer look at what would happen to a plane on each one.
The Sun: This works about as well as you'd imagine. If the plane is released close enough to the Sun to feel its atmosphere at all, it's vaporized in less than a second.
Mars: To see what happens to aircraft on Mars, we turn to X-Plane.
X-Plane is the most advanced flight simulator in the world. The product of 20 years of obsessive labor by a hardcore aeronautics enthusiast who uses capslock a lot when talking about planes, it actually simulates the flow of air over every piece of an aircraft’s body as it flies. This makes it a valuable research tool, since it can accurately simulate entirely new aircraft designs—and new environments.
In particular, if you change the X-Plane config file to reduce gravity, thin the atmosphere, and shrink the radius of the planet it can simulate flight on Mars. (Note: Thank you to Tom J and the folks in the X-Plane community for their help with aerodynamic calculations in different atmospheres.)
X-Plane tells us that flight on Mars is difficult, but not impossible. NASA knows this, and has considered surveying Mars by airplane. The tricky thing is that with so little atmosphere, to get any lift, you have to go fast. You need to approach Mach 1 just to get off the ground, and once you get moving, you have so much inertia that it’s hard to change course—if you turn, your plane rotates, but keeps moving in the original direction. The X-Plane author compared piloting Martian aircraft to flying a supersonic ocean liner.
Our Cessna 172 isn’t up to the challenge. Launched from 1 km, it doesn’t build up enough speed to pull out of a dive, and plows into the Martian terrain at over 60 m/s (135 mph). If dropped from four or five kilometers, it could gain enough speed to pull up into a glide—at over half the speed of sound. The landing would not be survivable.
Venus:Unfortunately, X-Plane is not capable of simulating the hellish environment near the surface of Venus. But physics calculations give us an idea of what flight there would be like. The upshot is: Your plane would fly pretty well, except it would be on fire the whole time, and then it would stop flying, and then stop being a plane.
The atmosphere on Venus is over 60 times denser than Earth’s, which is thick enough that a Cessna moving at running speed would rise into the air. Unfortunately, the air it’s rising into is hot enough to melt lead. The paint would start melting off in seconds, the plane’s components would fail rapidly, and the plane would glide gently into the ground as it came apart under the heat stress.
A much better bet would be to fly above the clouds. While Venus’s surface is awful, its upper atmosphere is surprisingly Earthlike. 55 kilometers up, a human could survive with an oxygen mask and a protective wetsuit; the air is room temperature and the pressure is similar to that on Earth mountains. You need the wetsuit, though, to protect you from the sulfuric acid. (I’m not selling this well, am I?)
The acid's no fun, but it turns out the area right above the clouds is a great environment for an airplane, as long as it has no exposed metal to be corroded away by the sulfuric acid. And is capable of flight in constant Category-5-hurricane-level winds, which are another thing I forgot to mention earlier.
Venus is a terrible place.
Jupiter: Our Cessna can’t fly on Jupiter; the gravity is just too strong. The power needed to maintain level flight is three times greater than that on Earth. Starting from a friendly sea-level pressure, we’d accelerate through the tumbling winds into a 275 m/s (600 mph) downward glide deeper and deeper through the layers of ammonia ice and water ice until we and the aircraft were crushed. There's no surface to hit; Jupiter transitions smoothly from gas to solid as you sink deeper and deeper.
Saturn: The picture here is a bit friendlier than on Jupiter. The weaker gravity—close to Earth’s, actually—and slightly denser (but still thin) atmosphere mean that we’d be able to struggle along a bit further before we gave in to either the cold or high winds and descended to the same fate as on Jupiter.
Uranus: Uranus is a strange, uniform bluish orb. There are high winds and it’s bitterly cold. It’s the friendliest of the gas giants to our Cessna, and you could probably fly for a little while. But given that it seems to be an almost completely featureless planet, why would you want to?
Neptune: If you’re going to fly around one of the ice giants, Neptune (Motto: “The Slightly Bluer One”) is probably a better choice than Uranus. It at least has some clouds to look at before you freeze to death or break apart from the turbulence.
Titan: We’ve saved the best for last. When it comes to flying, Titan might be better than Earth. Its atmosphere is thick but its gravity is light, giving it a surface pressure only 50% higher than Earth’s with air four times as dense. Its gravity—lower than that of the Moon—means that flying is easy. Our Cessna could get into the air under pedal power.
In fact, humans on Titan could fly by muscle power. A human in a hang glider could comfortably take off and cruise around powered by oversized swim-flipper boots—or even take off by flapping artificial wings. The power requirements are minimal—it would probably take no more effort than walking.
The downside (there’s always a downside) is the cold. It’s 72 kelvin on Titan, which is about the temperature of liquid nitrogen. Judging from some numbers on heating requirements for light aircraft, I estimate that the cabin of a Cessna on Titan would probably cool by about two degrees per minute.
The batteries would help to keep themselves warm for a little while, but eventually the craft would run out of heat and crash. The Huygens probe, which descended with batteries nearly drained (taking fascinating pictures as it fell), succumbed to the cold after only a few hours on the surface. It had enough time to send back a single photo after landing—the only one we have from the surface of a body beyond Mars.
If humans put on artificial wings to fly, we might become Titan versions of the Icarus story—our wings could freeze, fall apart, and send us tumbling to our deaths.
this is the best reason for a moon colony
But I've never seen the Icarus story as a lesson about the limitations of humans. I see it as a lesson about the limitations of wax as an adhesive. The cold of Titan is just an engineering problem. With the right refitting, and the right heat sources, a Cessna 172 could fly on Titan—and so could we.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
When - if ever - will the bandwidth of the Internet surpass that of FedEx?
—Johan Öbrink
Never underestimate the bandwidth of a station wagon full of tapes hurtling down the highway.
–Andrew Tanenbaum, 1981
If you want to transfer a few hundred gigabytes of data, it’s generally faster to FedEx a hard drive than to send the files over the internet. This isn’t a new idea—it’s often dubbed SneakerNet—and it’s how Google transfers large amounts of data internally.
But will it always be faster?
Cisco estimates that total internet traffic currently averages 167 terabits per second. FedEx has a fleet of 654 aircraft with a lift capacity of 26.5 million pounds daily. A solid-state laptop drive weighs about 78 grams and can hold up to a terabyte.
That means FedEx is capable of transferring 150 exabytes of data per day, or 14 petabits per second—almost a hundred times the current throughput of the internet.

gifs of animals falling off of things, volume 1
If you don’t care about cost, this ten-kilogram shoebox can hold a lot of internet
We can improve the data density even further by using MicroSD cards:

glug glug glug glug
Those thumbnail-sized flakes have a storage density of up to 160 terabytes per kilogram, which means a FedEx fleet loaded with MicroSD cards could transfer about 177 petabits per second, or two zettabytes per day—a thousand times the internet’s current traffic level. (The infrastructure would be interesting—Google would need to build huge warehouses to hold a massive card-processing operation.)
Cisco estimates internet traffic is growing at about 29% annually. At that rate, we’d hit the FedEx point in 2040. Of course, the amount of data we can fit on a drive will have gone up by then, too. The only way to actually reach the FedEx point is if transfer rates grow much faster than storage rates. In an intuitive sense, this seems unlikely, since storage and transfer are fundamentally linked—all that data is coming from somewhere and going somewhere—but there’s no way to predict usage patterns for sure.
While FedEx is big enough to keep up with the next few decades of actual usage, there’s no technological reason we can’t build a connection that beats them on bandwidth. There are experimental fiber clusters that can handle over a petabit per second. A cluster of 200 of those would beat FedEx.
If you recruited the entire US freight industry to move SD cards for you, the throughput would be on the order of 500 exabits—half a zettabit—per second. To match that transfer rate digitally, you’d need take half a million of those petabit cables.
So the bottom line is that for raw bandwidth, the internet will probably never beat SneakerNet. Of course, the virtually infinite bandwidth would come at the cost of 80,000,000-millisecond ping times.

1000ms of lag lets you dodge shots; 100000000 lets you win a game, play through a whole tournaments, and build and maintain quality friendships before they have a chance to react
the first thing we did getting in Panama was to go swim naked from a not so private beach (and at the time i'm writing this, we just came back from being seen again by this khmer guy in thma bang)
If the Hubble telescope were aimed at the Earth, how detailed would the images be?
—Kyle Rankin
This is a common question. The Hubble operators get it a lot, and their FAQ page answers it. The problem isn’t—as some people say—that the Earth is too bright. As Phil Plait of Bad Astronomy pointed out, Hubble looks at Earth pretty regularly.
The real problem is that Hubble is moving over the surface at over 7 kilometers per second. Even a short exposure would be a blur.
That’s no fun. Is there a way we could make it work? I decided to take a closer look.
As our picture target, we’ll use this typical desk:

a picture of a typical desk
The Earth’s atmosphere won’t be a problem. It’s actually much more of a problem for surface-based telescopes looking at space than for space-based telescopes looking at the surface. The reason for this is geometric:
a diagram of atmospheric distortion
Hubble is the best visible-light telescope we have, but its resolution does have limits. Pluto, out in the Kuiper belt, lies right at those limits. The best pictures we have of Pluto come from Hubble, but the ex-planet is still little more than a mysterious blur.
At that resolution (about 0.05 arcseconds, give or take) and Hubble’s distance from the desk (about 570 kilometers) the desk would look like this:

this desk is apparently in a glass house
But that desk is also zooming by, so even a perfect image will be blurred:

who would live in a glass house
Combining the two effects gives us an end result that looks like this:

people who live in glass houses shouldn't be trusted with other decisions, given that they decided to live in a glass house
That’s no good.
Could we rotate Hubble to track the surface, and eliminate the blur?
Hubble swivels to follow targets. Usually, they’re far enough away that we can assume they’re at infinite distance. The automatic on-board parallax algorithms can’t handle targets closer than about ten times the distance to the Moon. When astronomers want to use it to take pictures of the Moon, sometimes they send it commands to rotate manually, then turn on the camera mid-maneuver.
It doesn’t work very well. Moving Hubble at those speeds is cumbersome with the current guidance package. The resulting photos are better than what you can see with the naked eye, but they’re not very good by Hubble standards. Here’s our desk, with the image degraded by a similar amount that the Moon one was:

a frosted glass house might make sense
Fortunately, the Moon is bright enough that if you’ll settle for a short exposure, you can avoid the problem. This photo was taken with a half-second exposure, short enough that it didn’t have to do much in the way of tracking.
Unfortunately, our desk is moving across the telescope’s field of view about 600 times faster than the Moon. Tracking is unavoidable.
The strange thing is, the desk really isn’t moving all that fast. Hubble is just really slow. To track the surface, it would need to rotate less than a degree per second at maximum.
But Hubble wasn’t built for surface tracking. The telescope’s top rotational (“slew”) speed is only a few degrees per minute (about the speed of a minute hand on a clock) and even those speeds are fast enough that its gyroscopes cause it to vibrate, which destroys the image quality.
Clearly, we’d need to disable Hubble’s guidance system and bolt on our own control system. Hubble’s rotational moment of inertia is similar to that of a small carousel; too hard for the existing gyroscopes to move, but not hard in the absolute sense. With our custom control system, it could be made to track the surface, and get photos pretty close to optimal quality:

But this isn’t just a hypothetical situation.
Much of the technology in military spy satellites is believed to be similar to that of Hubble. So in a sense, pointing a Hubble-type telescope at the surface is not only possible—it’s what the US government actually does.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
How much would the sea level fall if every ship were removed all at once from the Earth's waters?
—Michael Toje
About six microns—slightly more than the diameter of a strand of spider silk.
a diagram showing that if you remove all the ships from the ocean the water will uncover spider silk and bacteria
Archimedes’ principle tells us that the water displaced by a ship weighs as much as the ship itself. If we can figure out the total weight of all the world’s ships, we can figure out how much water they’re displacing, then divide that volume by the surface area of the ocean to figure out how much the water level would drop.
Weighing ships is confusing. There are a bunch of different measurements of the size of a ship, and many of them, like gross tonnage, are actually measures of the volume of the ship’s rooms and other internal spaces, not its weight.
The UN Conference on Trade and Development publishes estimates of the size of the world shipping fleet.
What the UNCTD publishes is “deadweight tonnage”, which is the maximum weight of the ship’s fuel, cargo, and crew. What we want is “displacement”. Unfortunately, comprehensive numbers for displacement are harder to find.
Fortunately, we can estimate it. Brian Barrass’s book Ship Design and Performance for Masters and Mates gives a table of ratios of deadweight tonnage to displacement for different types of ships.
Extrapolating from the last few years of UNCTD data, and using the coefficients from the book, suggests that the world fleet weighs about 2.15 billion tons when fully loaded. The main component of the fleet by weight is oil tankers and bulk ore-carrying ships, which make up over two-thirds of the total. (The UNCTD data doesn’t include small recreational boats or naval fleets. However, based on some numbers for naval fleets and recreational boats, neither one contributes much to the total.)
A ton of water is about a cubic meter. 2.15 billion cubic meters divided by the surface area of the oceans equals about 6 microns (0.006 mm).
But you don’t have to worry about that six-micron sea level drop. The oceans are currently rising at about 3.3 millimeters per year due to global warming (through both glacial melting and thermal expansion of seawater).
At that rate (normalized for seasonal variation and short-term fluctations), if you removed every ship from the ocean, the water would be back up to its original average level in 16 hours.
a graph showing that you can't fix sea-level rise by putting a bunch of boats on a mountain
Sea levels will likely rise a few feet by the year 2100. Current fish wet biomass is about 2 billion tons, so removing them won’t make a dent either. (Marine fish biomass dropped by 80% over the last century, which—taking into consideration the growth rate of the world’s shipping fleet—leads to an odd conclusion: Sometime in the last few years, we reached a point where there are, by weight, more ships in the ocean than fish.)
And what about the old joke about how much deeper the ocean would be without sponges? While estimates of sponge biomass are hard to come by, the answer is probably that if you removed all the sponges, sea level would drop by no more than a few microns ... and much less if you squeezed them out first.

do you know how much deeper the ocean would be if we dropped in everyone who repeats that sponge joke?
we lied together to go diving together and this liveaboard was awesome. we were fantasizing about colombia and met colombians, about whales and saw whales and the whale shark, and the monkeys, and the obese crocodile...
How many unique English tweets are possible? How long would it take for the population of the world to read them all out loud?
—Eric H., Hopatcong, NJ
High up in the North in the land called Svithjod, there stands a rock. It is a hundred miles high and a hundred miles wide. Once every thousand years a little bird comes to this rock to sharpen its beak. When the rock has thus been worn away, then a single day of eternity will have gone by.
—Hendrik Willem Van Loon
Tweets are 140 characters long. There are 26 letters in English—27 if
you include spaces. Using that alphabet, there are  possible strings.
possible strings.
But Twitter doesn't limit you to those characters. You have all of
Unicode to play with, which has room for over a million different
characters. The way Twitter counts Unicode characters is
complicated, but the
number of possible strings could be as high as 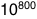 .
.
Of course, almost all of them would be meaningless jumbles of characters from a dozen different languages. Even if you're limited to the 26 English letters, the strings would be full of meaningless jumbles like "ptikobj". Eric's question was about tweets that actually say something in English. How many of those are possible?
This is a tough question. Your first impulse might be to allow only English words. Then you could further restrict it to grammatically valid sentences.
But it gets tricky. For example, “Hi, I’m Mxyztplk” is a grammatically valid sentence if your name happens to be Mxyztplk. (Come to think of it, it’s just as grammatically valid if you’re lying.) Clearly, it doesn’t make sense to count every string that starts with “Hi, I’m ...” as a separate sentence. To a normal English speaker, “Hi, I’m Mxyztplk” is basically indistinguishable from “Hi, I’m Mxzkqklt”, and shouldn't both count. But “Hi, I’m xPoKeFaNx” is definitely recognizably different from the first two, even though “xPoKeFaNx” isn’t an English word by any stretch of the imagination.
Fortunately, there’s a better approach.
Let’s imagine a language which has only two valid sentences, and every tweet must be one of the two sentences. They are:
Twitter would look like this:
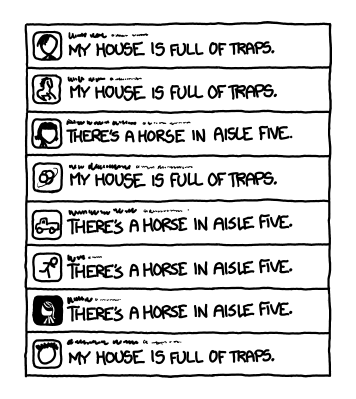
i once knew a little internet community that repeated the same six lines of conversation, in the same order, for over ten years, while having their actual conversation in their posts' title lines
The messages are relatively long, but there’s not a lot of information in each one—all they tell you is whether the person decided to send the trap message or the horse message. It’s a 1 or a 0. Although there are a lot of letters, for a reader who knows the pattern the language carries only one bit of information per sentence.
This example hints at a very deep idea, which is that information is fundamentally tied to the recipient’s uncertainty about the message’s content and their ability to predict it in advance.
Claude Shannon—who almost singlehandedly invented modern information theory—had a clever method for measuring the information content of a language. He showed groups of people samples of typical written English which were cut off at a random point, then asked them to guess which letter came next.

a volcano threatens to flood a town with information
Based on the rates of correct guesses—and rigorous mathematical analysis—Shannon determined that the information content of typical written English was around 1.0 to 1.2 bits per letter. This means that a good compression algorithm should be able to compress ASCII English text—which is eight bits per letter—to about 1/8th of its original size. Indeed, if you use a good file compressor on a .txt ebook, that’s about what you’ll find.
If a piece of text contains n bits of information, in a sense it
means that there are 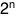 different messages it can convey.
There’s a bit of mathematical juggling here (involving, among other
things, the length of the message and the concept of unicity
distance), but the
bottom line is that it suggests there are on the order of about
different messages it can convey.
There’s a bit of mathematical juggling here (involving, among other
things, the length of the message and the concept of unicity
distance), but the
bottom line is that it suggests there are on the order of about 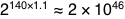 meaningfully different
English tweets, rather than
meaningfully different
English tweets, rather than 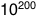 or
or 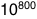 .
.
Now, how long would it take the world to read them all out?
Reading 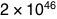 tweets would take a person nearly
tweets would take a person nearly 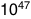 seconds. It’s such a staggeringly large number of tweets
that it hardly matters whether it’s one person reading or a billion—they
won’t be able to make a meaningful dent in the list in the lifetime of
the Earth.
seconds. It’s such a staggeringly large number of tweets
that it hardly matters whether it’s one person reading or a billion—they
won’t be able to make a meaningful dent in the list in the lifetime of
the Earth.
Instead, let’s think back to that bird sharpening its beak on the mountaintop. Suppose that the bird scrapes off a tiny bit of rock from the mountain when it visits every thousand years, and it carries away those few dozen dust particles when it leaves. (A normal bird would probably deposit more beak material on the mountaintop than it would wear away, but virtually nothing else about this scenario is normal either, so we’ll just go with it.)
Let’s say you read tweets aloud for 16 hours a day, every day. And behind you, every thousand years, the bird arrives and scrapes off a few invisible specks of dust from the top of the hundred-mile mountain with its beak.
When the mountain is worn flat to the ground, that’s the first day of eternity.
The mountain reappears and the cycle starts again for another eternal
day. 365 eternal days—each one 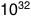 years long—makes an
eternal year.
years long—makes an
eternal year.

years go by so quickly
100 eternal years, in which the bird grinds away 36,500 mountains, make an eternal century.
But a century isn’t enough. Nor a millennium.
Reading all the tweets takes you ten thousand eternal years.
That’s enough time to watch all of human history unfold, from the invention of writing to the present, with each day lasting as long as it takes for the bird to wear down a mountain.
140 characters may not seem like a lot, but we will never run out of things to say.

where do you go the rest of the time, bird?
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
What would happen if a hair dryer with continuous power was turned on and put in an airtight 1x1x1 meter box?
—Dry Paratroopa
A typical hair dryer draws 1875 watts of power.
All 1875 watts have to go somewhere. No matter what happens inside the box, if there’s 1875 watts of power being used, eventually there will be 1875 watts of heat flowing out.
This is true of any device that uses power, which is a handy thing to know. For example, people worry about leaving disconnected chargers plugged into the wall for fear that they’re draining power. Are they right? You can use heat flow to come up with simple rule of thumb: If an unused charger isn’t warm to the touch, it’s using less than a penny of electricity a day. For a small smartphone charger, if it’s not warm to the touch, it’s using less than a penny a year.
This is true of almost any powered device (though not necessarily those plugged into a second device. If a charger is connected to something, like a smartphone or laptop, power can be flowing from the wall through the charger into the device.)
But back to the box.
Heat will flow from the hair dryer out into the box. If we assume the dryer is indestructible, the interior of the box will keep getting hotter until the outer surface reaches about 60°C (140°F). At that temperature, the box will be losing heat to the outside as fast as the hair dryer is adding it inside, and the system will be in equilibrium.
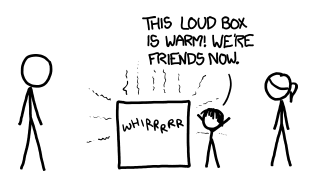
it's warmer than my parents! it's my new parents.
The equilibrium temperature will be a bit cooler if there’s a breeze, or if the box is sitting on a wet or metallic surface that conducts away heat quickly.
If the box is made of metal, 60°C is hot enough to burn your hand if you touch it for more than five seconds. If it’s wood, you can probably touch it for a while, but there’s a danger that parts of the box in contact with the mouth of the hair dryer will catch fire.
The inside of a box will be like an oven. The temperature it reaches will depend on the thickness of the box wall; the thicker and more insulating the wall, the higher the temperature. It wouldn’t take a very thick box to create temperatures high enough to burn out the hair dryer.
But let’s assume an indestructible hair dryer. And if we have something as cool as an indestructible hair dryer, it seems like a shame to limit it.
anything is possible with tape
With 18,750 watts flowing out of the hair dryer, the surface of the box reaches over 200°C (475°F), as hot as a skillet on low-medium.
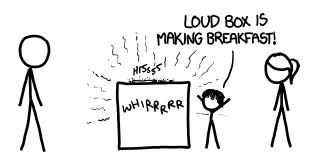
new momdad is great!
I wonder how high this dial goes.
there's a distresing amount of space left on the dial
The surface of the box is now 600°C, hot enough to glow a dim red.

the box is glowing
If it’s made of aluminium, the inside is starting to melt. If it’s made of lead, the outside is starting to melt. If it’s on a wood floor, the house is on fire. But it doesn't matter what's happening around it; the hair dryer is indestructible.
the box is glowing more
Two megawatts pumped into a laser is enough to destroy missiles.
At 1300°C, the box is now about the temperature of lava.

the box is looking melty
One more notch.
this hair dryer is probably not up to code
18 megawatts are flowing into the box.

the box exudes a pleasant yellow glow
The surface of the box reaches 2400°C. If it were steel, it would have melted by now. If it’s made of something like tungsten, it might conceivably last a little longer.
Just one more, then we'll stop.

the hair dryer is turned to 187 megawatts, somehow
187 megawatts is enough to make the box glow white. Not a lot of box materials can survive these conditions, so we’ll have to assume the box is indestructible.

the floor is made of lava
Unfortunately, the floor isn’t.
Before it can burn its way through the floor, someone throws a water balloon under it. The burst of steam launches the box out the front door and onto the sidewalk. (Note: If you’re ever trapped with me in a burning building, and I suggest an idea for how we could escape the situation, it’s probably best to ignore me.)
settings are added with reckless abandon
1.875 gigawatts (I lied about stopping). According to Back to the Future, the hair dryer is now drawing enough power to travel back in time.

a tiny star sits in a pool of fire
The box is blindingly bright, and you can’t get closer than a few hundred meters due to the intense heat. It sits in the middle of a growing pool of lava. Anything within 50-100 meters bursts into flame. A column of heat and smoke rise high into the air. Periodic explosions of gas beneath the box launch it into the air, and it starts fires and forms a new lava pool where it lands.
more settings are added via some impressively durable tape
18.7 gigawatts. The conditions around the box are similar to those on the pad during a Space Shuttle launch. The box begins to be tossed around by the powerful updrafts it’s creating.
In 1914, H.G. Wells imagined devices like this in his book The World Set Free. He wrote of a type of bomb that, instead of exploding once, exploded continuously, a slow-burn inferno that started inextinguishable fires in the hearts of cities. The story eerily foreshadowed the development, 30 years later, of nuclear weapons.
hair dryers left plugged in have been known to start fires, but rarely so enthusiastically as this one
The box is now soaring through the air. Each time it nears the ground, it superheats the surface, and the plume of expanding air hurls it back into the sky.
the un has expressed concern that rogue states may gain access to hair dryer power dial labeling technology
1.875 terawatts is like a house-sized stack of TNT going off every second.

we're running out of space, fortunately
A trail of firestorms—massive conflagrations which sustain themselves by creating their own wind systems—winds its way across the landscape.
A new milestone: The hair dryer is now, impossibly, consuming more power than every other electrical device on the planet combined.

that's the last one, right?
The box, soaring high above the surface, is putting out energy equivalent to three Trinity tests every second.
At this point, the pattern is obvious. This thing is going to skip around the atmosphere until it destroys the planet.
Let's try something different.

the dial is turned back to zero
We turn the dial to zero as the box is passing over northern Canada. Rapidly cooling, it plummets to Earth, landing in Great Bear Lake with a plume of steam. And then …

every dial goes to 11 if you turn it hard enough
This one goes to 11. Petawatts, in this case.
A brief story:
The official record for fastest manmade object is the Helios 2 probe, which reached about 70 km/s in a close swing around the Sun. But it’s possible the actual holder of that title is a two-ton metal manhole cover.
The cover sat atop a shaft at an underground nuclear test site operated by Los Alamos as part of Operation Plumbbob. When the one-kiloton nuke went off below, the facility effectively became a nuclear potato cannon, giving the cap a gigantic kick. A high-speed camera trained on the lid caught only one frame of it moving upward before it vanished—which means it was moving at a minimum of 66 km/s. The cap was never found.
66 km/s is about six times escape velocity, but contrary to the linked blog’s speculation, it’s unlikely the cap ever reached space. Newton’s impact depth approximation suggests that it was either destroyed completely by impact with the air or slowed and fell back to Earth.
Our suddenly-activated hair dryer box, bobbing in lake water, undergoes a similar process. The heated steam below it expands outward, and as the box rises into the air, the entire surface of the lake turns to steam. The steam, heated to a plasma by the flood of radiation, accelerates the box faster and faster.
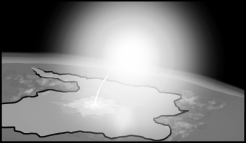
photo courtesy cmdr. hadfield
Rather than slam into the atmosphere like the manhole cover, the flood of radiation heats the air around it, creating a bubble of expanding plasma which offers little resistance. The box exits the atmosphere and continues away, slowly fading from second sun to dim star. Much of the Northwest Territories is burning, but the Earth has survived.
Although we may wish we hadn't.

the bill is about $20 trillion, give or take
and we went on to develop the fig bar theory in san blas as we spent days lying in the sun, swimming together and eating cookies
How much cornstarch can I rinse down the drain before unpleasant things start to happen?
—Anna R., Fort Wayne, IN
It depends what you consider unpleasant.
If you watered down the cornstarch enough, you could likely pour it down the drain for years without any ill effects. If it didn’t clog the sink, the rest of the pipes could probably handle it. It might provoke some confusion among the sewage treatment people, but it wouldn’t break anything.
But it’d be terrifically boring (and thus unpleasant) to pour cornstarch down a sink all day, so I guess that’s—

the questioner pours cornstarch into a drain
… Oh. Huh.
Well, let’s thicken the cornstarch.
When you mix cornstarch and water in a bit under a 2:1 ratio, you get oobleck, a substance with some odd physical properties. This is a great kitchen science experiment everyone should try at least once.
At low speeds, oobleck behaves like a liquid. If you gently swish your fingers in a bowl of it, it feels like milk or heavy cream. However, if you make a fist and punch the surface, your hand bounces off with a thud—it’s like hitting a slab of raw meat.
If you vibrate oobleck, even stranger things happen.
It wouldn’t take much of the mixture to clog a drain. It depends on your plumbing, but you could probably stop up your sink with a small bowl of it.
Since your drain is clogged, I guess that’s the answer to your question.
the drain is clogged but it's ok
Well, ok. I guess some people don’t mind clogged drains.
If you keep at it, after a few minutes, your sink will overflow, spilling goop onto your floor.

let the cornstarch hit the floor
Financially, this will be hard to keep up. If you’re mixing as fast as the water will come out of the sink, this project may cost you in the neighborhood of $5,000 per day if you can’t find a good bulk distributor.

by the time you read this, bitcoins will be either hilariously expensive or hilariously cheap
At this rate, it should build up on the floor at a rate of an inch or two per day.

pouring cornstarch into the sink is endless fun
If your doors are sealed well, it will continue to build up. Once it reaches knee height (a week or two after you started), you may be able to hold the rising tide at bay for a little bit—at least in one room—by getting someone to flush the toilet repeatedly. The pipes there are larger and harder to clog; the limiting factor would probably be how fast the tank filled with water.

this is probably a violation of your lease
Eventually, after a month or two, the oobleck would reach the living room window. The pressure would quickly rise, and sooner or later the window would burst.
As the deadly Boston Molasses Flood proved, even thick, viscous fluids can flow quickly when in large enough quantities. The oobleck would pour rapidly out onto the lawn, carrying you with it.
At this point, the local officials would probably notice and, at the very least, shut off your water.

be careful of the broken glass while you're being swept out through the window
But I guess if you really like cornstarch that much, nothing unpleasant has happened.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
What if you somehow managed to make a stereo travel at twice the speed of sound, would it sound backwards to someone who was just casually sitting somewhere as it flies by?
—Tim Currie
Yes.
Technically, anyway. It would be pretty hard to hear.
The basic idea is pretty straightforward. The stereo is going faster than its own sound, so it will reach you first, followed by the sound it emitted one second ago, followed by the sound it emitted two seconds ago, and so forth.
the cone defined by the edge of the run-together overlapping circles is the shockwave that makes a sonic boom as it sweeps along the ground
The problem is that the stereo is moving at Mach 2, which means that two seconds ago, it was over a kilometer away. It’s hard to hear music from that distance, particularly when your ears were just hit by (a) a sonic boom, and (b) pieces of a rapidly disintegrating stereo.
Wind speeds of Mach 2 would messily disassemble most consumer electronics. The force of the wind on the body of the stereo is roughly comparable to that of a dozen people standing on it:

this is the vibe that most of my parties have
An ordinary stereo wouldn’t make it, but one with some kind of ruggedized high-strength casing might be able to survive.
If we put together a durable, heavy-duty stereo and launch it on a ballistic trajectory, it will only be traveling at supersonic speeds for the first 150 meters or so. This means that the target will hear a maximum of about a third of a second of reversed music.
This phenomenon is actually confirmed in the 2008 paper Reproduction of Virtual Sound Sources Moving at Supersonic Speeds in Wave Field Synthesis, which says that the sound wave field “contains a component carrying a time-reversed version of the source’s input signal”.
The sonic boom would be the first thing the target would hear. It would be followed by several sounds played over one another, including both reversed music (rising slightly in pitch as it fades out) and forward-playing music (which would play at half speed and an octave too low), followed by the crash of a stereo demolishing your neighbor’s shed.
Which means that if you’re playing one of those albums containing secret demonic messages, the result will be the strangest listening experience of your life:

my cabbages!
i like you
With today's technology, would it be possible to launch an unmanned mission to retrieve Voyager I?
—Elliott Bennett
Voyager I is farther from Earth than any other manmade object. After getting a pair of gravitational kicks from Jupiter and Saturn, it’s headed out of the Solar System at a pretty high speed, and nothing else we’ve built is on track to pass it.
Strangely, as of the day I’m writing this, Voyager is actually getting closer to us, because Earth is in a part of its orbit where it’s approaching Voyager faster than Voyager is fleeing. But in a few months, we’ll swing around the Sun and Voyager will again be getting farther away.
Earth is faster than Voyager but only goes in circles.
It has a 35-year head start, so it would be hard to catch. But catching up isn’t the problem.
New Horizons, the spacecraft currently headed out of the Solar System by way of Pluto, is never going to catch up to Voyager—it’s not moving fast enough and it’s headed in the wrong direction. But it could have.
The reason Voyager is moving so fast is that it got gravitational assists from Jupiter and Saturn, while New Horizons only got one from Jupiter.
Voyager gets a boost from Jupiter and a ball gets a boost from a truck.
Gravity assists aren’t paradoxical magic. It’s just like bouncing a tennis ball off a passing truck. Gyroscopes, on the other hand, ARE magic.
If New Horizons had ditched the Pluto objective and waited for the right planetary alignment (the 2030s look promising), it could have swung by Jupiter and Saturn, then caught up to Voyager in as little as a century or two! (Assuming we could manage to hit Voyager from that far away. But I bet we could; our rocket scientists are pretty good at rocket science.)
Of course, getting there’s the easy part. The hard part is getting back.
Voyager weighs a little less than a ton and is moving away at 17 kilometers per second (if it were in the atmosphere, that would be Mach 50). And since it’s out in interstellar space, there are no speeding Jupiters to grab on to. Stopping Voyager is going to take a lot of fuel.
It’s what engineers call the tyranny of the rocket equation: As the amount that you want to change your speed (“delta-v”) goes up, the fuel required increases exponentially. The equation tells us that to turn the 720-kilogram Voyager around, we’re going to need at least 30 tons of fuel.
But to get that fuel out there, we need even more fuel. And to get that fuel, we need even more fuel. (This is where the tyrannical rocket equation gets its exponential term.) In fact, to rescue Voyager, we’d have to launch a fleet of—at minimum—60 New Horizons-sized spacecraft loaded with nothing but fuel.
Could we do it? Sure. There are a couple plausible ways. Instead of building five to ten dozen fuel-laden Titan IIIEs, we could just build a fleet of ten or fifteen Saturn Vs, and do the whole thing with fewer launches. But however we did it, it would be a massive and expensive operation similar in scale to the Apollo program.
The difference between the launch vehicle we’d used to get Voyager out of the Solar System and the fleet we’d need for a round trip is striking:

there and there and back again
Fortunately, there’s one way around the tyranny of the rocket equation: Ditch the rockets.
Ion engines—which use electric fields to accelerate exhaust gas to high speeds—are far more efficient than chemical rockets, and they make accelerating to high speeds much more plausible.
The reason we’re not using them for everything is that they produce very little thrust, so it takes a long time to get up to speed. It’s like if you had a car that gets amazing mileage but has a one-horsepower engine. (Actually, are you sure that’s not just a horse?) Ion engines are great; the current ones just take forever to get you moving.
But since catching Voyager is going to take a long time anyway, ion engines are fine. We could launch a probe (like this one), send it out to Voyager, latch on, turn everything around, and let it spend a few decades slowing Voyager down.
Once Voyager had lost nearly all its speed, the Sun’s gravity would take over, and the probe would begin a long slow slide toward the inner Solar System. This would take about 200 years, and with some extremely careful nudges, we could make sure it falls in an Earth-crossing orbit.
Two centuries later, Voyager would reach Earth and, with no way to slow down, burn up in our atmosphere, because we didn’t think to send out an aerobraking shell with the rescue craft. So that was a waste of a few centuries of work and billions upon billions of dollars.

A returning Voyager becomes a very expensive firework.
Maybe a better idea would be to borrow a salvage vessel and set sail for the coast of New South Wales, Australia. There, in the waters off Jervis Bay, the Australian Royal Navy ship Voyager sank in 1964 after an accidental collision.
That one’s probably easier to retrieve.

NASA goes sailing
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
How hard would a puck have to be shot to be able to knock the goalie himself backwards into the net?
—Tom
This can’t really happen.
It’s not just a problem of hitting it hard enough. This blog isn’t concerned with that kind of limitation. Humans with sticks can’t make a puck go much faster than about 50 meters per second, so we’ll assume this puck is launched by a hockey robot or an electric sled or a hypersonic light gas gun.
The problem, in a nutshell, is that hockey players are heavy and pucks are not. A goalie in full gear outweighs a puck by a factor of about 600. Even the fastest slap shot has less momentum than a ten-year-old skating along at a mile per hour.
Hockey players also can brace pretty hard against the ice. A player skating at full speed can stop in the space of a few meters, which means the force they’re exerting on the ice is pretty substantial. (It also suggests that if you started to slowly tilt a hockey rink, it could get up to 50 degrees before the players would all slide to one end. Clearly, experiments are needed to confirm this.)
From estimates of collision speeds in hockey videos, and some guidance from a hockey player friend, I estimated that the 165-gram puck would have to be moving somewhere between Mach 2 and Mach 8 to knock the goalie backward into the goal—faster if the goalie is bracing against the hit, and slower if the puck hits at an upward angle.
Firing an object at Mach 8 is not, in itself, very hard. One of the best methods for doing so is the aforementioned hypersonic gas gun, which is—at its core—the same mechanism a BB gun uses to fire BBs.

and world peace, which i recognize my first request makes significantly less likely
But a hockey puck moving at Mach 8 will have a lot of problems. It’s not on the same scale as a relativistic baseball, but the air ahead of the puck would be compressed and heated very rapidly. It wouldn’t be going fast enough to ionize the air and leave a glowing trail like a meteor, but the surface of the puck would (given enough time) start to melt or char.
The air resistance, however, will slow the puck down very quickly, so a puck going at Mach 8 when it leaves the launcher might be going a fraction of that when it arrives at the goal. And even at Mach 8, the puck probably wouldn’t pass through the goalie’s body. Instead, it would burst apart on impact with the power of a large firecracker or small stick of dynamite.
If you’re like me, when you first saw this question, you might’ve imagined the puck leaving a cartoon-style hockey-puck-shaped hole. But that’s because our intuitions are shaky about how materials react at very high speeds.
Instead, a different mental picture might be more accurate: Imagine throwing a ripe tomato—as hard as you can—at a cake.

...goal?
That’s about what would happen.
we said good bye
Am I right to be afraid of pressure cookers? What's the worst thing that can happen if you misuse a pressure cooker in an ordinary kitchen?
—Delphine Lourtau
The worst thing?

why are you humming ice ice baby?
Pressure cookers are dangerous.
They can explode, in a sense, but not as violently as you might fear (or hope). The pressure inside a consumer cooker doesn’t go above about two atmospheres—about the pressure inside a can of soda. Those levels can be dangerous, but they’re generally not high enough to cause the metal to violently rupture.
So what makes a pressure cooker dangerous?
Imagine a world where Pepsi is scalding hot. Now imagine that someone shakes up a can of Pepsi and sets it in front of you.

the first thing i’d do in this world is try the diet coke and mentos thing
That’s the real threat from a pressure cooker: If the seal fails (or the lid is opened too early), it can spray scalding stew in all directions.
But it’s not really an explosion.
The blast couldn’t even fling the lid very far. If you mounted a rifle-style barrel on a pressure cooker, even in ideal circumstances it wouldn’t be able to fire the lid much faster than you could throw it. Any potato cannon (especially this one) could do better.
Of course, the question wasn’t about whether a pressure cooker is likely to explode. It was about what the worst thing that could happen was.
If you disable the safety valve, there are plenty of ways to produce much more dangerous pressures. You could completely fill it with water and heat it, fill it with Drano and aluminum foil, or just pump in air from a compressor.
The result would depend on your pressure cooker. Chances are it would start to leak. If it didn’t, and it somehow stayed together up a few hundred atmospheres (pressures typical of scuba tank), when it finally ruptured it could easily kill you.

frankly, we're surprised she survived this long
Even so, that’s far from the worst thing you could do with a pressure cooker.
Frankly, there are so many options it would be impossible to survey them all. But for my money, one of the most horrifying things you could do is this:
(Note: Never try this, for reasons which will become obvious in a moment.)
Fill the cooker with oxygen up to 5 PSI, then pump in fluorine until it starts escaping through the safety valve. Put the vessel over an open flame until it reaches 700°C (That’s °C, not °F. Yes, this will probably set off the smoke alarm.) Now, pump the hot gas over a liquid-oxygen-cooled stainless steel surface.
The procedure here is a little tricky, but if you do things right, the gas will condense into dioxygen difluoride (O2F2).
And that stuff is awful.
Ray Bradbury taught us that paper burns when exposed to oxygen at temperatures above 451°F. Dioxygen difluoride is so volatile that it makes almost any organic substance ignite and explode at any temperature hotter than 300°F below zero. It can literally make ice catch fire.
In an article about O2F2, Chemistry blogger Derek Lowe (of the excellent In The Pipeline) used phrases like “violently hideous”, “deeply alarming”, and “chemicals that I never hope to encounter”. Another article refers to fluorine as “the gas of Lucifer”, and lists chemists who were poisoned or blown up while attempting to work with it.
If your house is heated by natural gas, and it happens to contain hydrogen sulfide, you could pipe some of it into your container of O2F2. In addition to a massive explosion, this will also produce a cloud of hydrogen fluoride gas. Hydrogen fluoride can dissolve human tissue on contact, starting with your lungs and corneas.
As Lowe points out, the chemistry of this kind of reaction (O2F2 and sulfides) is largely unexplored.
Which gives us an answer to our question. What’s the worst thing that can happen in a pressure cooker?

i’m expecting this contraption to get me a nobel prize, assuming it proves powerful enough to blow open the safe where they’re kept.
Science.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
If everybody in the US drove west, could we temporarily halt continental drift?
—Derek

two figures pondering windmills
Thanks to plate tectonics, the United States is drifting west at about a centimeter per year. (The people who live there, on the other hand, are on average drifting west at about a centimeter per minute.)
There are 212,309,000 licensed drivers in the US, and since we have more cars than drivers, we can in theory get them all behind the wheel at once. The average car on the road weighs a hair over 4,000 lbs, so we have 850 billion pounds of car (plus around 30 billion pounds of driver) to throw around.
The North American plate, by comparison, is about 25 million square
kilometers in area and probably averages around 35 kilometers thick.
Given a density of about 2.7 kg/Liter, its mass is probably in the
neighborhood of 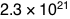 kg, so it outweighs our fleet by a
factor of about six trillion.
kg, so it outweighs our fleet by a
factor of about six trillion.
cars drive west, every one driven by someone with that song in their head
But let's say we give it a shot anyway, and all 212 million of us point our vehicles due west and then floor it. For the dozen or so seconds we’d spend accelerating to freeway speed, our cars would exert very close to a trillion newtons of eastward force on the ground. In the absence of other forces, conservation of momentum tells us it would accelerate the plate up to a blistering 18 cm/year, more than enough to reverse the current motion.
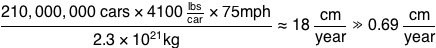
But wait. The plates are moving so slowly that their motion isn’t dominated by momentum. They’re held where they are by a balance of forces—the complicated and boring ones from the beginning—and if we’re going to stop them, we probably have to try to figure out what they are. If the plates were drifting along as if they were sliding on ice, then we could push them easily. But it’s possible they’re locked on a slow-but-steady magma conveyer belt, and we can’t move them back without also shifting the flow beneath them.
It was only recently—in the mid-20th century—that we discovered that continents move at all, and we’re still getting a handle on the complex forces between the plates and currents in the mantle that control continental motion. But they sound pretty complicated so let’s try to ignore them. We don’t care how it works—we just want to know if we can break it.
These forces are hard to measure, so we’re not sure how they all work. There’s some evidence that the flow of the mantle along the bottom of the plates isn’t as important as the weight of the edges of the crust as it sinks into the mantle, and the forces in the mantle pushing back against it.
The geology literature gives us some loose estimates to work with. The
drag from the mantle, resisting forward motion, is typically in the
neighborhood of 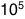 to
to 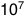 newtons per square meter,
meaning the existing eastward drag force on the North American plate is
on the order of
newtons per square meter,
meaning the existing eastward drag force on the North American plate is
on the order of  newtons.
newtons.
That’s millions of times more than our fleet. The other forces are greater still. The fact that plates move steadily along in the face of drag that powerful suggests to me that the equilibrium of forces guiding them is probably fairly stable and unlikely to be responsive by our little shove.
But conservation of momentum still works—so something has to move, and that something is the entire Earth, whose rotation would be sped up slightly. If our fleet were centered at around 39º N, the day would be shortened by only about 200 attoseconds—about a trillionth of a percent of the time it took you to read the word “attosecond.” If we drove east instead, the day would be lengthened by a similar amount.
But considering the gasoline required, those 200 attoseconds would cost at least $50 billion. At 100 octillion times minimum wage, that’s a pretty bad hourly rate.
All things considered, it would be a lot easier to just forget to change our clocks next spring and get a whole hour for nothing.

if we charged a fair interest rate on the hour we gave up every spring we'd get 1.02 hours back every fall
through our emails, we got closer and closer every day, i liked you like i had never liked anyone before
What is the longest possible sunset you can experience while driving, assuming we are obeying the speed limit and driving on paved roads?
—Michael Berg
To answer this, we have to be sure what we mean by “sunset".
This is a sunset:
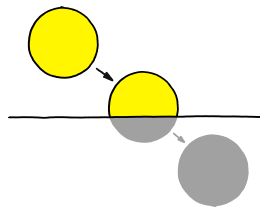
this is a sunset
This is not a sunset:

this is not a sunset
For the purposes of our question, this is not a sunset:

the sun changes its mind and goes back to bed
This is also not a sunset:
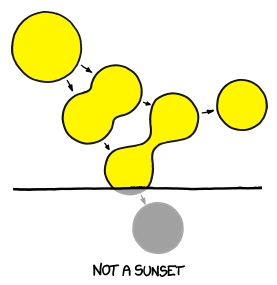
this is half a sunset
This is definitely not a sunset:

you bred sun-raptors?
And no matter what happens here, this will not be a sunset:

aww, man, you didn’t even let me try
Sunset starts the instant the Sun touches the horizon, and ends when it disappears completely. If the Sun touches the horizon and then lifts back up, the sunset is disqualified.
For a sunset to count, the Sun has to set behind the idealized horizon, not just behind a nearby hill. This is not a sunset, even though it seems like one:
the sun can’t hide
The reason that can’t count as a sunset is that if you could use arbitrary obstacles, you could cause a sunset whenever you wanted by hiding behind a rock.
Note: We also have to consider refraction. The Earth’s atmosphere bends light, so when the Sun is at the horizon it appears about one Sun-width higher than it would otherwise. The standard practice seems to be to include the average effect of this in all calculations, which I’ve done here.
At the Equator in March and September, sunset is a hair over two minutes long. Closer to the poles, in places like the London, it can take between 200 and 300 seconds. It’s shortest in spring and fall (when the Sun is over the equator) and longest in the summer and winter.
If you stand still at the South Pole in early March, the Sun stays in the sky all day, making a full circle just above the horizon. Sometime around March 21st, it touches the horizon for the only sunset of the year. This sunset takes 38-40 hours, which means it makes more than a full circuit around the horizon while setting.
But Michael’s question was very clever. He asked about the longest sunset you can experience on a paved road. There’s a road to the research station at the South Pole, but it’s not paved—it’s made of packed snow. There are no paved roads anywhere near either pole.
The closest road that really qualifies is probably the main road in Longyearbyen, on the island of Svalbard, Norway. (The end of the airport runway in Longyearbyen gets you slightly further, although driving there might get you in trouble.)
Longyearbyen is actually closer to the North Pole than McMurdo Station in Antarctica is to the South Pole. There are a handful of military, research, and fishing stations further north, but none of them have much in the way of roads; just airstrips, which are usually gravel and snow.
If you putter around downtown Longyearbyen (get a picture with the “polar bear crossing” sign), the longest sunset you could experience would be a few minutes short of an hour. It doesn’t actually matter if you drive or not; the town is too small for your movement to make a difference.
But if you head a little ways south, you can do even better.
If you start driving from the tropics and stay on paved roads, the furthest north you can get is the tip of European Route 69 in Norway. There are a number of roads crisscrossing northern Scandinavia, so that seems like a good place to start. But which road should we use?
Intuitively, it seems like we want to be as far north as possible. The closer we are to the pole, the easier it is to keep up with the Sun.
Unfortunately, it turns out keeping up with the Sun isn’t a good strategy. Even in those high Norwegian latitudes, the Sun is just too fast. At the tip of European Route 69—the farthest you can get from the Equator while driving on paved roads—you’d still have to drive at about half the speed of sound to keep up with the Sun. (And E69 runs north-south, not east-west, so you’d drive into the Barents Sea anyway.)
Luckily, there’s a better approach.
If you're in northern Norway on a day when the Sun just barely sets and then rises again, the terminator (day-night line) moves across the land in this pattern:
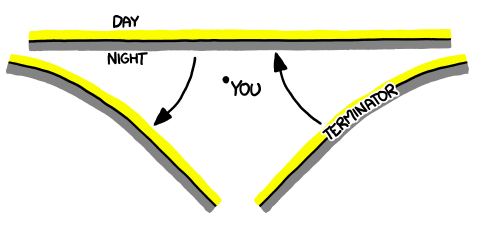
a drawing of you lit by the setting sun
(Not to be confused with the Terminator, which moves across the land in this pattern:)
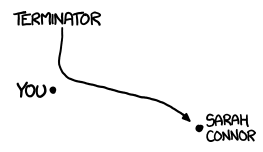
I can’t decide which terminator I’d rather have to run from
To get a long sunset, the strategy is simple: Wait for the date when the terminator will just barely reach your position. Sit in your car until the terminator reaches you, drive north to stay a little ahead of it for as long as you can (depending on the local road layout), then u-turn and drive back south fast enough that you can get past it to the safety of darkness. (These instructions also work for the other kind of Terminator.)
Surprisingly, this strategy works about equally well anywhere inside the Arctic Circle, so you can get this lengthy sunset on many roads across Finland and Norway. I ran a search for long-sunset driving paths using PyEphem and some GPS traces of Norwegian highways. I found that over a wide range of routes and driving speeds, the longest sunset was consistently about 95 minutes—an improvement of about 40 minutes over the Svalbard sit-in-one-place strategy.
But if you are stuck in Svalbard and want to make the sunset—or sunrise—last a little longer, you can always try spinning counterclockwise. It’s true that it will only add an immeasurably small fraction of a nanosecond. But depending on who you’re with ...

cause of death: stumbled dizzily into the path of a polar bear
... it might be worth it.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
Could a high-speed train run through a vertical loop, like a rollercoaster, with the passengers staying comfortable?
—Gero Walter
No.
Since this is kind of a disappointing answer, I tried relaxing the requirements a little.
Could a high-speed train run through a vertical loop, like a rollercoaster, with the passengers staying comfortable surviving?
Still no.
Could a modified and reinforced high-speed train with a jet engine on top run through a vertical loop, like a rollercoaster, with the passengers staying comfortable surviving?
Maybe.
The Norwegian aluminium and energy company Norsk Hydro ran a pro-education ad in which a bunch of kids build a giant roller-coaster loop on a train track as a prank. This is, of course, unrealistic, but not just for the obvious reasons. There are some problems with the whole idea of sending high-speed trains through loops.
The first issue is geometry. The biggest vertical loop which a train could conceivably go around has a radius of about 200 meters. If it’s any bigger than that, even the fastest trains will fail to complete the loop.
Unfortunately, a 200 meter loop is much too tight. Most high-speed trains are limited to vertical curves with radii no shorter than 20 kilometers.
two possible loops, neither of which is a good idea
The reason for those limits isn't that trains aren't bendy enough. It's how fast they're going.
The spec sheet for the Bombardier ZEFIRO, for example, says it can handle a pretty tight vertical curve radius—just 900 meters. At the train’s top speed, that curve would create about two gees of acceleration. This might be survivable (for the passengers, at least, if not the train), but it would certainly not be comfortable.
Yet a 900 meter radius loop is still too big. Even with the engine at full power, the train wouldn’t even be able to get a quarter of the way around the loop before sliding back down.
the little engine that let everyone down
The CGI train in the Norwegian video is an Di 4, which is shown moving about twice as fast as it can actually go. Based on its speed and number of cars, the loop appears to have a radius of about 70 meters, which is part of why it’s shown going so fast—the actual Di 4 would be just a little too slow, and would fall off the track at the top. The digital one, however, makes it around the loop in about five seconds, no problem.
But the tight loop means the passengers and train are experiencing between 9 and 15 gees. This is at the limit of what fighter pilots can handle in pressure suits. In addition to killing everyone on board, it would certainly destroy the train, to say nothing of the track. 70 meters is much too tight.
Clearly, we need a larger loop. 900 meters would be great, but our trains aren’t fast enough for that.\
But maybe we could make the train go faster ...
Hmm.
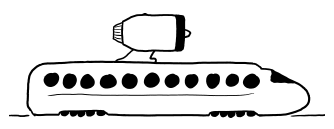
this is a good idea
Believe it or not, this has been tried before—a number of countries have built jet-engine-powered trains. Sadly, they never took off. Fortunately, they never took off.
A 747 engine mounted atop a bullet train would probably add about 35% to its speed. Is that enough to do a 900-meter loop?
i will diminish, and go into the west, and remain a train
Nope.
Ok, putting the jet engine on top didn’t work. Maybe we should try something different.
a train with a jet engine underneath
... why did we think that would work? Forget that idea.
Clearly, we need some combination of a fast train and a medium-sized loop. The sweet spot for loop size and shape is probably something like this:
pay attention, norwegian kids!
Of course, given the height, we’d probably have to build it into a small mountain:

a diagram of the internal structure of NORAD
The shape of the loop, which is common in roller coasters, would spread out the g-forces more evenly, resulting in a max of only a few gees—totally survivable!
Of course, the construction costs would be astronomical, and it goes without saying that no group of kids could pull it off alone without the resources of a major government.
To any Norwegian kids reading this who were hoping to build a train loop, don't despair—there may still be a way to make this happen.
The US Vice President, Joe Biden, served in the US Senate for 36 years. In all that time, he never moved to Washington, DC. Instead, every night, he took the train home to Delaware to see his family. This is very touching, but after the first few years, I'm sure the commute got a little dull.
So, if you’re looking for a high-level backer to help you make someone’s train ride a little more exciting, you might just try talking to Joe.
going to see my familyyyyyyyyyyyyyeeeeeeeeeeeeeeeee
i recognized us in the pelikan song Sie mögen sich
How high can a human throw something?
—Irish Dave on the Isle of Man
Humans are good at throwing things. In fact, we’re great at it; no other animal can throw stuff like we can.
It's true that chimpanzees hurl feces (and, on rare occasions, stones), but they’re not nearly as accurate or precise as humans. [1] [2] Antlions throw sand, but they don’t aim it. Archerfish hunt insects by throwing water droplets, but they use specialized mouths instead of arms. Horned lizards shoot jets of blood from their eyes for distances of up to five feet. I don’t know why they do this because whenever I reach the phrase “shoot jets of blood from their eyes” in an article I just stop there and stare at it until I need to lie down.

AAAAAAAAAAAAAA
So while there are other animals that use projectiles, we’re just about the only animal that can grab a random object and reliably nail a target. In fact, we’re so good at it that some researchers have suggested rock-throwing played a central role in the evolution of the modern human brain.[3][4]
Throwing is hard. In order to deliver a baseball to a batter, a pitcher has to release the ball at exactly the right point in the throw. A timing error of half a millisecond in either direction is enough to cause the ball to miss the strike zone.[5]
To put that in perspective, it takes about five milliseconds for the fastest nerve impulse to travel the length of the arm.[6] That means that when your arm is still rotating toward the correct position, the signal to release the ball is already at your wrist. In terms of timing, this is like a drummer dropping a drumstick from the 10th story and hitting a drum on the ground on the correct beat.

wrong kind of drumstick but hey, i like the sound.
We seem to be much better at throwing things forward than throwing them upward. Since we’re going for maximum height, we could use projectiles that curve upward when you throw them forward; the Aerobie Orbiters I had when I was a kid often got stuck in the highest treetops. But we could also sidestep the whole problem by using a device like this one:
a mechanism for hitting yourself in the head with a baseball after a four-second delay
It could be a springboard, a greased chute, or even a dangling sling—anything that redirects the object upward without adding to—or subtracting from—its speed. Of course, we could also try this:
i just came in to get a glass of water let me down
But the deflector box seems easier.
I ran through the basic aerodynamic calculations for a baseball thrown at various speeds. I will give these in units of giraffes:

recommended SI unit for altitude
The average person can probably throw a baseball at least three giraffes high:

top-tier giraffes
Someone with a reasonably good arm could manage five:

order your giraffe stacks now
A pitcher with an 80 mph fastball could manage ten giraffes:
act now while supplies are still cooperative
Aroldis Chapman, the holder of the world record for fastest recorded pitch (105 mph), could in theory launch a baseball 14 giraffes high:
buy one from the top rows and get a bottom-row one free
But what about projectiles other than a baseball? Obviously, with the aid of tools like slings, crossbows, or the curved xistera scoops in jai alai, we can launch projectiles much faster than that. But for this question, let’s assume we stick to bare-handed throwing.
A baseball is probably not the ideal projectile, but it’s hard to find speed data on other kinds of thrown objects. Fortunately, a British javelin thrower named Roald Bradstock held a random object throwing competition, in which he threw everything from dead fish to an actual kitchen sink. Bradstock’s experience gives us a lot of useful data (and a lot of other data, too). In particular, it suggests a potentially superior projectile: A golf ball.
Few professional athletes have been recorded throwing golf balls. Fortunately, Bradstock has, and he claims a record throw (to first contact with the ground) of 170 yards.[7] This involved a running start, but even so, it’s reason to think that a golf ball might work better than a baseball. It makes sense; the limiting factor in baseball pitches is the torque on the elbow, and the lighter golf ball might allow the pitching arm to move slightly faster.
The speed improvement from using a golf ball instead of a baseball would probably not be very large, but it seems plausible that a professional pitcher with some time to practice could throw a golf ball faster than a baseball.
If so, based on aerodynamic calculations, Aroldis Chapman could probably throw a golf ball about sixteen giraffes high:
one giraffe per tier plus Aroldis plus you makes a team
This is probably about the maximum possible altitude for a thrown object.
… unless you count the technique by which any five-year-old can beat all these records easily:

just 98 more
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
Is this the most expensive music video ever?
—Various Youtube commenters
For starters, a big welcome home to Chris Hadfield, who returned to Earth last night after a memorable stint as commander of the International Space Station.
Commander Hadfield’s video performance of Space Oddity was an instant hit, and prompted many commenters to ask whether it should count as the most expensive music video ever made.
At a total lifetime cost in the neighborhood of \$150 billion [1], the International Space Station is one of the world’s most expensive megaprojects. (The exact cost is hard to pin down, since the countries contributing don’t all handle their finances the same way.)
By comparison, the most expensive music videos have production budgets in the range of a few million dollars. If Commander Hadfield’s video gets the ISS’s entire \$150 billion price tag, then it must be tens of thousands of times more expensive than the runner-up, right?
Not so fast.
The ISS is expensive, but there have been music videos set against an even more expensive backdrop.
At a cost of roughly \$400 billion, the US Eisenhower Interstate Highway System is probably the most expensive peacetime public works project in the history of mankind. If we’re including the entire ISS in the cost of Commander Hadfield’s video, any video shot on the American highway system should get the cost of the highway system added to its total.
By that measure, the commander’s video would lose to U2’s Last Night on Earth, which was filmed on a section of I-670 in Missouri,[2] and therefore cost more than the ISS and the Moon landing program combined.
In both cases, the comparison doesn’t really make sense; both the ISS and the US highway system are used for things other than making music videos.[citation needed] Instead, let’s look at some other ways we could calculate the cost of Hadfield’s video.
If you spread out the ISS’s price tag across all the astronaut-hours spent on board, you come up with about \$7.5 million per person per day, or roughly \$90 per second.[3] That sounds like a lot, but at that rate, the five-and-a-half-minute video only runs about \$30,000. Given that the video has probably done more for space industry than millions in public outreach, that’s a good deal.
Hadfield’s son confirmed that Hadfield shot the video himself with no help from other astronauts, so even if we assume he spent several hours setting it up and recording it, we don’t come close to the \$7 million cost of the video Michael and Janet Jackson made for Scream.
And the truth is, this isn’t a very good way to calculate costs either. Presumably, Commander Hadfield isn’t busy commanding things 24/7. He has some free time, and it’s no skin off anyone’s back how he spends it (assuming his hobby isn’t drilling holes in walls). It’s hard to argue that shooting the video cost anyone \$90/second when he was going to be up there floating around anyway.
Why do we even have that drill?
Alternately, we could look at how much Commander Hadfield was paid to make the video. As a Canadian astronaut, his salary is somewhere between \$145,200 and \$171,000 CAD.[4] Astronaut work hours are a little atypical, but if we assume that in the long run he’s on the job 40 hours a week, that works out to \$85/hour. By that measure, the cost of the video was \$7.84. Not 7.84 million; 7 dollars and 84 cents (\$7.76 US).

UNSCHEDULED BURN
And then there’s the guitar.
While it’s hard to argue that the entire cost of the ISS counts toward the video, we could at least include the cost to launch the guitar. The Larrivée Parlor acoustic guitar in the video went up years ago on the Space Shuttle, and astronauts have been playing it ever since.[5] Given that launch costs at the time were between \$20,000 and \$30,000 per pound, the cost to send up the guitar was probably in the neighborhood of \$75,000.
While that’s far from the most anyone’s paid for a guitar,[6] it’s certainly a lot of money. And if playing music helps the astronauts relax and keep from going crazy while they’re crammed together in a tin can for months at a time, it’s probably a worthwhile investment.
Of course, this plan could backfire.

There’s a sign on the Soyuz coming up: NO WONDERWALL.
we wanted to study together, maybe have a learning mini community
I've been told that if the Earth were shrunk down to the size of a bowling ball, it would be smoother than said bowling ball. My question is, what would a bowling ball look like if it were blown up to the size of the Earth?
—Seth C.
A good, professional-quality bowling ball is smoother than the Earth.
Phil Plait, of Bad Astronomy, took a look at the claim that the Earth was smoother than a billiard ball. He concluded that the Earth was smoother but less round, based on published billiard ball roundness tolerances. However, he couldn’t find any information on the size and shape of a billiard ball’s pits and bumps.
Fortunately for us, there are people who digitally scan bowling ball surfaces.

I digitally scan bowling ball surfaces and I vote.
These scans (along with various measurements of ball roughness[1] tell us that a high-end bowling ball is quite smooth. If blown up to the scale of the Earth, the ridges and bumps[2] would be between 10 and 200 meters high, and the peaks would be between one and three kilometers apart:
If you rolled a bowling ball down one of those hills, that would be pretty meta.
By Earth standards, this is quite smooth; our highest mountains are 40 times higher.
What would this bowling ball world (we’ll call it “Lebowski”) be like?
For starters, bowling balls are a lot less dense than rock, so Lebowski’s surface gravity would be a quarter the strength of Earth’s:

Maybe you can also do this on Earth. I don’t want to try.
It would also (at first) have no atmosphere.

You’re out of your element.
The finger holes would be about a thousand kilometers across and a few thousand kilometers deep.
A hole in the world.
On Earth, holes this big would expose the molten interior. But Lebowski doesn’t have a molten interior.
The Earth’s core is hot for two reasons: It’s still glowing from the heat of all the dust collapsing together when it formed, and it’s full of radioactive metals. Lebowski wouldn’t have either of these, so its core would start out cold.
The holes would be far too big to hold themselves open against gravity; On that scale, the polymers in the bowling ball would behave more like a liquid. In the space of about half an hour, the holes would undergo a slow-motion collapse.
This is no longer, by any stretch of the imagination, a regulation ball.
As they collapsed, the material around the holes would heat to a glow. At the center of the hole, a white-hot jet of charred hydrocarbons would fountain outward into space.
When it was over, Lebowski would be left with massive scars, each marking the location where an abyss collapsed to form a molten sea.
The shattered visage of Lebowski.
And now, thanks to this question, whenever I look at the Moon, I’ll notice the Sea of Tranquility, the Sea of Serenity, and the Sea of Crisis, and I’ll think: Finger holes.
But that’s just, like, my opinion, man.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
Let's assume there's life on the the nearest habitable exoplanet and that they have technology comparable to ours. If they looked at our star right now, what would they see?
—Chuck H.
Answer:

a pale yellow dot
Let’s try a more complete answer. We’ll start with ...
Radio transmissions
Contact popularized the idea of aliens listening in on our transmissions. Sadly, the odds are against it.
Here’s the problem: Space is big. Really big.[1]
You can work through the physics of interstellar radio attenuation, but the problem is captured pretty well by considering the economics of the situation: If your TV signals are getting to another star, you’re losing money. Powering a transmitter is expensive, and creatures on other stars aren’t buying the products in the TV commercials that pay your electricity bill.
The full picture is more complicated, but the bottom line is that as our technology has advanced, less of our radio traffic has been leaking out into space. We’re closing down the giant transmitting antennas and switching to cable and fiber and tightly-focused cell-tower networks.[2]
While our TV signals may have been detectable—with great effort—for a while,[3] that window is closing. In the late 20th century, when we were using TV and radio to scream into the void at the top of our lungs, the signal probably faded to undetectability after a few light-years.[4] The potentially habitable exoplanets we’ve spotted so far are dozens of light-years away, so the odds are they aren’t currently repeating our catchphrases.
But TV and radio transmissions still weren’t Earth’s most powerful radio signal. They were outshone by the beams from early-warning radar.[4]
Early-warning radar, a product of the Cold War, consisted of a bunch of ground and airborne stations scattered around the Arctic. These stations swept the atmosphere with powerful radar beams 24/7, often bouncing them off the ionosphere, and people obsessively monitored the echos for any hints of enemy movement. (I wasn’t alive during most of this period, but from what I hear, the mood was a little tense.)
These radar transmissions leaked into space, and could probably be picked up by nearby exoplanets[5] if they happened to be listening when the beam swept over their part of the sky. But the same march of technological progress that made the TV broadcast towers obsolete has had the same effect on early-warning radar. Today’s systems—where they exist at all—are much quieter, and may eventually be replaced completely by new technology.

<enemy frantically clicks to report account as spam>
Earth’s most powerful radio signal is the beam from the Arecibo telescope. This massive dish in Puerto Rico can function as a radar transmitter, bouncing a signal off nearby targets like Mercury and the asteroid belt. It’s essentially a flashlight which we shine on planets to see them better. (This is just as crazy as it sounds.)
But it transmits only occasionally, and in a narrow beam. If an exoplanet happened to be caught in the beam, and they were lucky enough to be pointing a receiving antenna at our corner of the sky at the time, all they would pick up would be a brief pulse of radio energy, then silence.
So hypothetical aliens looking at Earth probably wouldn’t pick us up with radio antennas.
But there’s also ...
Visible light
This is more promising. The Sun is really bright [citation needed] and its light illuminates the Earth.[citation needed] Some of that light is reflected back into space as “Earthshine”. Some of it skims close to our planet and passes through our atmosphere before continuing on to the stars. Both of these effects could potentially be detected from an exoplanet.[4][6]
They wouldn’t tell you anything about humans directly, but if you watched the Earth for long enough, you could figure out a lot about our atmosphere from the reflectivity. You could probably figure out what our water cycle looked like, and our oxygen-rich atmosphere would give you a hint that something weird was going on.
So in the end, the clearest signal from Earth might not be from us at all. It might be from the algae that have been terraforming the planet—and altering the signals we send into space—for billions of years.

Heeeey, look at the time. Gotta run.
Of course, if we wanted to send a clearer signal, we could. A radio transmission has the problem that they have to be paying attention when it arrives.
Instead, we could make them pay attention. With ion drives, nuclear pulse propulsion, or just clever use of gravitational slingshots, we could probably send a probe out of the Solar System fast enough to reach a given nearby star in a few dozen millennia. If we can figure out how to make a guidance system that survives the trip (which would be tough) we could use it to steer toward any inhabited planet.
To land safely, we’d have to slow down. But slowing down takes even more fuel. And, hey, the whole point of this was for them to notice us, right?
So maybe if those aliens looked toward our Solar System, this is what they’d see:

AAAAAAAAAAAAAAA
most of all we wanted to be together, it made sense
When (if ever) did the Sun finally set on the British Empire?
—Kurt Amundson
It hasn't. Yet. But only because of a few dozen people living in an area smaller than Disney World.
The world's largest empire
The British Empire spanned the globe. This led to the saying that the Sun never set on it, since it was always daytime somewhere in the Empire.
It's hard to figure out exactly when this long daylight began. The whole process of claiming a colony (on land already occupied by other people) is awfully arbitrary in the first place. Essentially, the British built their empire by sailing around and sticking flags on random beaches.[1] This makes it hard to decide when a particular spot in a country was "officially" added to the Empire.

“What about that shadowy place over there?” “That’s France. We’ll get it one of these days.”
The exact day when the Sun stopped setting on the Empire was probably sometime in the late 1700s or early 1800s, when the first Australian territories were added.[2]
The Empire largely disintegrated in the early 20th century, but—surprisingly—the Sun hasn't technically started setting on it again.
Fourteen territories
Britain has fourteen overseas territories, the direct remnants of the British Empire.[3]

A map showing the 0.386%% of Earth occupied by land.
(Many newly-independent British colonies joined the Commonwealth of Nations. Some of them, like Canada and Australia, have Queen Elizabeth as their official monarch. But they are independent states which happen to have the same queen; they are not part of any empire that they know of.)
The Sun never sets on all fourteen British territories at once (or even thirteen, if you don’t count the British Antarctic Territory). However, if the UK loses one tiny territory, it will experience its first Empire-wide sunset in over two centuries.
Every night, around midnight GMT, the Sun sets on the Cayman Islands, and doesn't rise over the British Indian Ocean Territory until after 1:00 AM. For that hour, the little Pitcairn Islands in the South Pacific are the only British territory in the Sun.
The Pitcairn Islands have a population of a few dozen people, the descendants of the mutineers from the HMS Bounty. The islands became notorious in 2004 when a third of the adult male population, including the mayor, were convicted of child sexual abuse.[4][5]
As awful as the islands may be, they remain part of the British Empire, and unless they're kicked out, the two-century-long British daylight will continue.
Will it last forever?
Well, maybe.
Four hundred years from now, in April of 2432, the island will experience its first total solar eclipse since the mutineers arrived.[6]
Luckily for the Empire, the eclipse happens at a time when the Sun is over the Cayman Islands in the Caribbean. Those areas won't see a total eclipse; the Sun will even still be shining in London.
In fact, no total eclipse for the next thousand years will pass over the Pitcairn Islands at the right time of day to end the streak. If the UK keeps its current territories and borders, it can stretch out the daylight for a long, long time.
But not forever. Eventually—many millennia in the future—an eclipse will come for the island, and the Sun will finally set on the British Empire.
![The walls of Buckingham Palace are lined with [in case of emergency, break glass] boxes. Inside each one is a cup of tea.](imgs/a/48/empire_eclipse.png)
The walls of Buckingham Palace are lined with [in case of emergency, break glass] boxes. Inside each one is a cup of tea.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
What would happen to the Earth if the Sun suddenly switched off?
—Many, many readers
This is probably the single most popular question submitted to What If.
Part of why I haven’t answered it is that it's been answered already. A Google search for what if the Sun went out turns up a lot of excellent articles thoroughly analyzing the situation.
However, since my recent articles on sunsets, the rate of submission of this question has risen even further, so I’ve decided to do my best to answer it.
If the Sun went out ...

Source: I'm going to go out on a limb and say 'The US Naval Observatory' on the assumption that no one there will read this.
We won’t worry about exactly how it happens. We'll just assume we figured out a way to fast-forward the Sun through its evolution so that it becomes a cold, inert sphere. What would the consequences be for us here on Earth?
Let's look at a few:
Reduced risk of solar flares: In 1859, a massive solar flare and geomagnetic storm hit the Earth.[1] Magnetic storms induce electric currents in wires. Unfortunately for us, by 1859 we had wrapped the Earth in telegraph wires. The storm caused powerful currents in those wires, knocking out communications and in some cases causing telegraph equipment to catch fire.[2]
Since 1859, we've wrapped the Earth in a lot more wires. If the 1859 storm hit us today, the Department of Homeland Security estimates the economic damage to the US alone would be several trillion dollars[3]—more than every hurricane which has ever hit the US combined.[4] If the Sun went out, this threat would be eliminated.
Improved satellite service: When a communications satellite passes in front of the Sun, the Sun can drown out the satellite's radio signal, causing an interruption in service.[5] Deactivating the Sun would solve this problem.
Better astronomy: Without the Sun, ground-based observatories would be able to operate around the clock. The cooler air would create less atmospheric noise, which would reduce the load on adaptive optics systems and allow for sharper images.
Stable dust: Without sunlight, there would be no Poynting–Robertson drag, which means we would finally be able to place dust into a stable orbit around the Sun without the orbits decaying. I’m not sure whether anyone wants to do that, but you never know.
Reduced infrastructure costs: The Department of Transportation estimates that it would cost $20 billion per year over the next 20 years to repair and maintain all US bridges.[6] Most US bridges are over water; without the Sun, we could save money by simply driving on a strip of asphalt laid across the ice.

It doesn't matter how thin the ice is when there's no cavity under it to fall into.
Cheaper trade: Time zones make trade more expensive; it's harder to do business with someone if their office hours don't overlap with yours.[7] If the Sun went out, it would eliminate the need for time zones, allowing us to switch to UTC and give a boost to the global economy.
Safer Children: According to the North Dakota Department of Health, babies younger than six months should be kept out of direct sunlight.[8] Without sunlight, our children would be safer.
Safer combat pilots: Many people sneeze when exposed to bright sunlight. The reasons for this reflex are unknown, and it may pose a danger to fighter pilots during flight.[9] If the Sun went dark, it would mitigate this danger to our pilots.
Safer parsnip: Wild parsnip is a surprisingly nasty plant. Its leaves contain chemicals called furocoumarins, which can be absorbed by human skin without causing symptoms ... at first. However, when the skin is then exposed to sunlight (even days or weeks later), the furocoumarins cause a nasty chemical burn. This is called phytophotodermatitis.[10] A darkened Sun would liberate us from the parsnip threat.

This is a good way to splatter your skin with furocoumarins.
In conclusion, if the Sun went out, we would see a variety of benefits across many areas of our lives.
Are there any downsides to this scenario?
We would all freeze and die.

It's the Sun. We need the Sun.
we kissed for the second first time in the streets of berlin, under the rain, looking for the light festival
What would it be like to navigate a rowboat through a lake of mercury? What about bromine? Liquid gallium? Liquid tungsten? Liquid nitrogen? Liquid helium?
–Nicholas Aron
Let's take these one at a time.
Bromine and mercury are the only known pure elements that are liquid at room temperature.
Rowing a boat on a sea of mercury just might be possible.
Mercury is so dense that steel ball bearings float on the surface. Your boat would be so buoyant that you'd barely make a dent in the mercury, and you'd have to lean your weight into the paddle to get the end of it below the surface.
'Michael, row the boat ashore.' 'I'm TRYING!'
In the end, it certainly wouldn't be easy, and you wouldn't be able to move fast. But you could probably row a little bit.
You should probably avoid splash fights.
Bromine is about as dense as water, so a standard rowboat could in theory float on it.
However, Bromine is awful. For one thing, it smells terrible; the name "bromine" comes from the ancient Greek "brōmos", meaning "stench". If that weren't enough, it violently reacts with a lot of materials. Hopefully, you're not in an aluminium rowboat.

The mercury one was going to be the least deadly, wasn't it.
If that's not incentive enough to avoid it, the Materials Safety Data Sheet on bromine includes the following phrases:
You should not get in a splash fight on a bromine lake.
Liquid gallium is weird stuff. Gallium melts just above room temperature, like butter, so you can't hold it in your hand for too long.
It's fairly dense, though not anywhere near as dense as mercury, and would be easier to row a boat on.
However, once again, you'd better hope the boat isn't made of aluminium, because aluminium (like many metals) absorbs gallium like a sponge absorbs water. The gallium spreads throughout the aluminium, dramatically changing its chemical properties. The modified aluminium is so weak it can be pulled apart like wet paper. This is something gallium has in common with mercury—both will destroy aluminium.
Like my grandma used to say, don't sail an aluminium boat on a gallium lake. (My grandma was a little strange.)
Liquid tungsten is really hard to work with.
Tungsten has the highest melting point of any element. This means there's a lot we don't know about its properties. The reason for this—and this may sound a little stupid—is that it's hard to study, because we can't find a container to hold it in. For almost any container, the material in the container will melt before the tungsten does. There are a few compounds, like tantalum hafnium carbide, with slightly higher melting points, but no one has been able to make a liquid tungsten container with them.
To give you an idea of how hot liquid tungsten is, I could tell you the exact temperature that it melts at (3422°C). But a better point might be this:
Liquid tungsten is so hot, if you dropped it into a lava flow, the lava would freeze the tungsten.
Needless to say, if you set a boat on a sea of liquid tungsten, both you and the boat would rapidly combust and be incinerated.
Liquid nitrogen is very cold.
Liquid helium is colder, but they're both closer to absolute zero than to the coldest temperatures in Antarctica, so to someone floating on them in a boat, the temperature difference is not that significant.
A Dartmouth engineering page on liquid nitrogen safety includes the following phrases:
Liquid nitrogen has a density similar to that of water, so a rowboat would float on it, but if you were in it, you wouldn't survive for long.
If the air above the nitrogen was room temperature when you started, it would cool rapidly, and you and the boat would be smothered in a thick fog as the water condensed out of the air. (This is the same effect that causes steam when you pour out liquid nitrogen.) The condensation would freeze, quickly covering your boat in a layer of frost.
The warm air would cause the nitrogen on the surface to evaporate. This would displace the oxygen over the lake, causing you to asphyxiate.
If the air (or the nitrogen) were both cold enough to avoid evaporation, you would instead develop hypothermia and die of exposure.
Liquid helium would be worse.
For one thing, it's only about one-eighth as dense as water, so your boat would have to be eight times larger to support a given weight.

Frankly, what they needed was a smaller shark.
But helium has a trick. When cooled below about two degrees kelvin, it becomes a superfluid, which has the odd property that it crawls up and over the walls of containers by capillary forces.
It crawls along at about 20 centimeters per second, so it would take the liquid helium less than 30 seconds to start collecting in the bottom of your boat.
This would, as in the liquid nitrogen scenario, cause rapid death from hypothermia.
If it's any consolation, as you lay dying, you would be able to observe an odd phenomenon.
Superfluid helium films, like the one rapidly covering you, carry the same types of ordinary sound waves that most materials do. But they also exhibit an additional type of wave, a slow-moving ripple that propogates along thin films of helium. It's only observed in superfluids, and has the mysterious and poetic name "third sound."
Your eardrums may no longer function, and wouldn't be able to detect this type of vibration anyway, but as you froze to death in the floor of a giant boat, your ears would be filled—literally—with a sound no human can ever hear: The third sound.
And that, at least, is pretty cool.
Worth it.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
What place on Earth would allow you to freefall the longest by jumping off it? What about using a squirrel suit?
—Dhash Shrivathsa
The largest purely vertical drop on Earth is the face of Canada's Mount Thor, which is shaped like this:
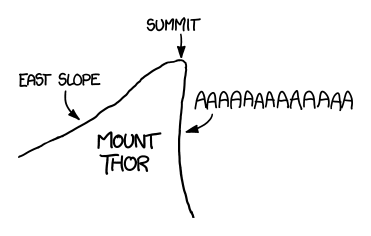
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
To make things a little less gruesome, let's suppose there's a pit at the bottom of the cliff, filled with something fluffy—like cotton candy—to safely break your fall.

Would this work? Stay tuned for a future article ...
A human falling with arms and legs outstretched has a terminal velocity in the neighborhood of 55 meters per second. It takes a few hundred meters to get up to speed, so it would take you a little over 26 seconds to fall the full distance.
What can you do in 26 seconds?
For starters, it's enough time to get all the way through the original Super Mario World 1-1,[Super Mario 1-1 speed run] assuming you have perfect timing and take the shortcut through the pipe.
It's also long enough to miss a phone call. Sprint's ring cycle—the time the phone rings before going to voicemail—is 23 seconds.[Sprint ring cycle] (For those keeping score, that means Wagner's is 2,350 times longer.)
If someone called your phone, and it started ringing the moment you jumped, it would go to voicemail three seconds before you reached the bottom.

Surprisingly good service for a desolate cliff face in Nunavut.
On the other hand, if you jumped off Ireland's 210-meter Cliffs of Moher, you would only be able to fall for about eight seconds—or a little more, if the updrafts were strong. That's not very long, but according to River Tam, given adequate vacuuming systems it might be enough time to drain all the blood from your body.
So far, we've assumed you're falling vertically. But you don't have to.
Even without any special equipment, a skilled skydiver—once they get up to full speed—can glide at almost a 45-degree angle.[Glide data] By gliding away from the base of the cliff, you could conceivably extend your fall substantially.
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA ::gasp:: AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
It's hard to say exactly how far; in addition to the local terrain, it depends heavily on your choice of clothes. As a comment on a BASE jumping records wiki puts it,
The record for longest [fall time] without a wingsuit is hard to find since the line between jeans and wingsuits has blurred since the introduction of more advanced ... apparel.
Which brings us to wingsuits—the halfway point between parachute pants and parachutes.
Wingsuits let you fall much more slowly. One wingsuit operator posted tracking data from a series of jumps.[Jump. Fly. Land., Air & Space] It shows that in a glide, a wingsuit can lose altitude as slowly as 18 meters per second—a huge improvement over the normal rate.
Even ignoring horizontal travel, that would stretch out our fall to over a minute. That's long enough for a chess game. It's also long enough to sing the first verse of—appropriately enough—REM's It's the End of the World as We Know It followed by—less appropriately—the entire breakdown from the end of the Spice Girls' Wannabe.

So here's the story / from A to Z / You wanna get with me / You gotta tumble helplessly
When we include horizontal glides, the times get even longer.
There are a lot of mountains that could probably support very long wingsuit flights. For example, Nanga Parbat, a mountain in Pakistan, has a drop of more than three kilometers at a fairly steep angle.[Prof. Dr. Herrligkoffer, The East Pillar of Nanga Parbat, The Alpine Journal (1984)] (Surprisingly, a wingsuit still works fine at those altitudes,[The Guestroom - Dr Glenn Singleman and Heather Swan] [Highest BASE jump: Valery Rozov breaks Guinness world record] though the jumper needs oxygen and glides a little faster than normal.)
So far, the record for longest wingsuit BASE jump is held by Dean Potter, who jumped from the Eiger—a mountain in Switzerland—and flew for three minutes and twenty seconds.[Dean Potter, Above It All]
What could you do with three minutes and twenty seconds?
Suppose we recruit Joey Chestnut and Takeru Kobayashi, the world's top competitive eaters.
If we can find a way for them to operate wingsuits while eating at full speed, and they jumped from the Eiger, they could—in theory—finish as many as 45 hot dogs between them before reaching the ground ... pass
Given the ongoing Kobayashi/Chestnut rivalry, the potential for sabotage could, somehow, make this situation even more dangerous.
... which would, if nothing else, earn them what just might be the strangest world record in history.
i like you
What if one were to drop 3,000 bouncy balls from a seven story parking structure onto a person walking on the sidewalk below? Should the person survive, what would be the number of bouncy balls needed to kill them? What injuries would occur and what would the associated crimes be?
—Ginger Bread
After falling from seven stories, the mass of bouncy balls would be moving at about 20 meters per second.
20 meters per second is about how fast an average person with a good arm could throw a bouncy ball. Therefore, to determine the result of an impact, we can make use of what Einstein called a gedankenexperiment, or "thought experiment":
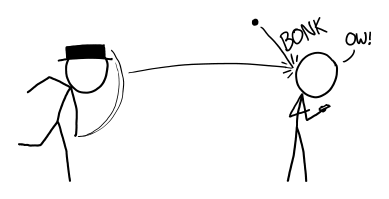
Careful calculations show that most of the motion of the target's head is due to flinching, not the momentum of the ball. Further calculations show that BONK.
In science, it's important that results be repeatable, so let's try that again:
The name 'Super Bowl' was originally a joking pun on 'super ball'.
The tricky thing about this scenario is that 3,000 one-inch bouncy balls is not as many as you probably think—it'd be enough to fill a large bucket.
This bucket would weigh about as much as a small child, which leads us to another gedankenexperiment:
![I want a poooonnnnnnyyyyyyy[WHAM]](imgs/a/52/bouncy_child.png)
I want a poooonnnnnnyyyyyyy[WHAM]
Of course, in reality, the average person can't throw a small child as fast as they can throw a bouncy ball.[citation needed] Furthermore, they won't all fall in one clump. If you poured the balls from a container, they would bounce around and spread out as they fell, and most of them would probably miss the target.
This effect was demonstrated in an experiment by Utah State University students, who poured 20,000 bouncy balls from a helicopter as part of their Geek Week. The balls fell as a cloud, rather than a single mass.
If you wanted to be sure of killing someone, you'd need a lot more balls. 3,000,000 of them—enough to fill a large room—would be be enough to guarantee that the target would either be crushed to death by the impact or buried too deep to dig themselves out.
To your last question, if someone just happened to walk underneath when you dropped the bouncy balls, and they were killed by the impact, you'd most likely be guilty of some form of manslaughter.
However, by asking this question, you've shown your intent to cause harm to the victim, demonstrating clear malice aforethought. By writing in to this blog, you've probably upgraded your charge to murder.
All in all, you should probably stick to gedankenexperiments.
STOP IT OW SCIENCE IS STUPID
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
How quickly would the ocean's drain if a circular portal 10 meters in radius leading into space was created at the bottom of Challenger Deep, the deepest spot in the ocean? How would the Earth change as the water is being drained?
–Ted M.
I want to get one thing out of the way first:
According to my rough calculations, if an aircraft carrier sank and got stuck against the drain, the pressure would easily be enough to fold it up[Extrapolated from the maximum pressure tolerable by icebreaker ship hull plates http://www.iacs.org.uk/document/public/Publications/Unified_requirements/PDF/UR_I_pdf410.pdf] and suck it through. Cooool.
Just how far away is this portal? If we put it near the Earth, the ocean would just fall back down into the atmosphere. As it fell, it would heat up and turn to steam, which would condense and fall right back into the ocean as rain. The energy input into the atmosphere alone would also wreak all kinds of havoc with our climate, to say nothing of the huge clouds of high-altitude steam.
So let's put the ocean-dumping portal far away—say, on Mars. (In fact, I vote we put it directly above the Curiosity rover; that way, it will finally have incontrovertible evidence of liquid water on Mars's surface.)
What happens to the Earth?
Not much. It would actually take hundreds of thousands of years for the ocean to drain.
Even though the opening is wider than a basketball court, and the water is forced through at incredible speeds,[xkcd.com/969] the oceans are huge. When you started, the water level would drop by less than a centimeter per day.
There wouldn't even be a cool whirlpool at the surface—the opening is too small and the ocean is too deep.[An experimental study of critical submergence to avoid free-surface vortices at vertical intakes] (It's the same reason you don't get a whirlpool in the bathtub until the water is more than halfway drained.)
But let's suppose we speed up the draining by opening more drains. (Remember to clean the whale filter every few days), so the water level starts to drop more quickly.
Let's take a look at how the map would change.
Here's how it looks at the start:
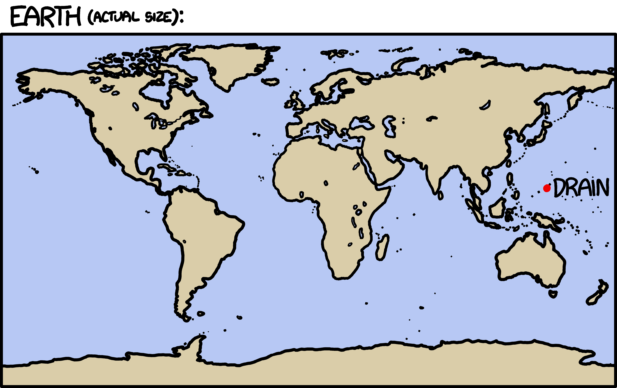
This is a Plate Carrée projection (c.f. xkcd.com/977)
And here's the map after the oceans drop 50 meters:
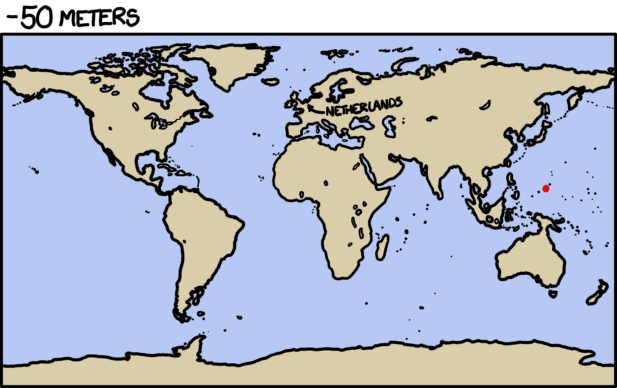
The British, fearing a Dutch conquest of the North Sea Plain, embark on a plan to build the dikes in the Netherlands higher so they can't get out.
It's pretty similar, but there are a few small changes. Sri Lanka, New Guinea, Great Britain, Java, and Borneo are now connected to their neighbors.
And after 2000 years of trying to hold back the sea, the Netherlands are finally high and dry. No longer living with the constant threat of a cataclysmic flood, they're free to turn their energies toward outward expansion. They immediately spread out and claim the newly-exposed land.
The Caspian Sea *is* rapidly shrinking, but that was happening long before we opened the drain.
When the sea level reaches (minus) 100 meters, a huge new island off the coast of Nova Scotia is exposed—the former site of the Grand Banks.
You may start to notice something odd: Not all the seas are shrinking. The Black Sea, for example, shrinks only a little, then stops.
This is because these bodies are no longer connected to the ocean. As the water level falls, some basins cut off from the drain in the Pacific. Depending on the details of the sea floor, the flow of water out of the basin might carve a deeper channel, allowing it to continue to flow out. But most of them will eventually become landlocked and stop draining.
The operation is briefly delayed while crews remove a blockage consisting of an estimated four hundred tons of hair.
At 200 meters, the map is starting to look weird. New islands are appearing. Indonesia is a big blob. The Netherlands now control much of Europe.
I feel like Japan should be called something other than an isthmus, but I can't find a better word for it.
Japan is now an isthmus connecting the Korean peninsula with Russia. New Zealand gains new islands. The Netherlands expand north.
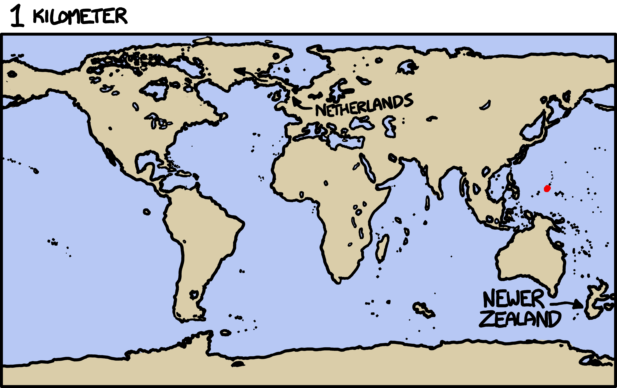
I always knew Greenland would one day betray Canada. And I'm pretty sure Baffin Island is a double agent working on Greenland's side.
New Zealand grows dramatically. The Arctic Ocean is cut off and its the water level stops falling. The Netherlands cross the new land bridge into North America.
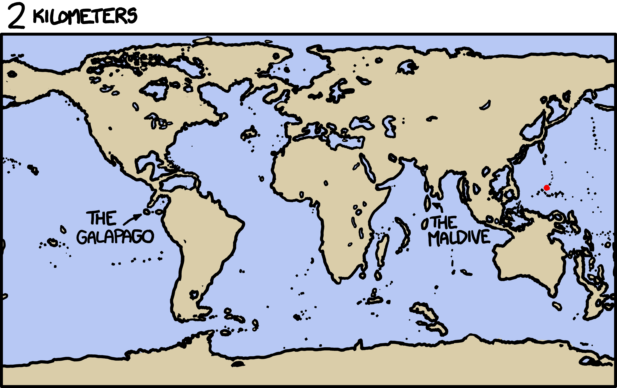
I'm not sure New Zealand even knows at this point.
The sea has dropped by two kilometers. New islands are popping up left and right. The Caribbean Sea and the Gulf of Mexico are losing their connections with the Atlantic. I don't even know what New Zealand is doing.
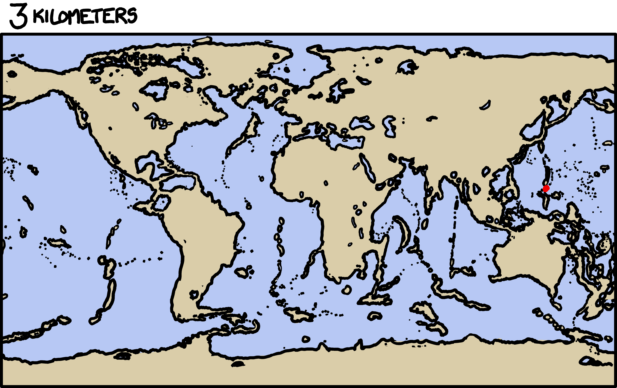
And Madagascar no longer looks like a car, which makes me sad.
At three kilometers, many of the peaks of the mid-ocean ridge—the world's longest mountain range—break the surface. Vast swaths of rugged new land emerge.
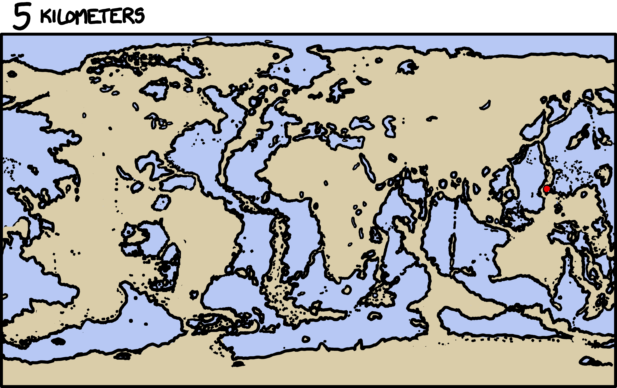
Raising the Titanic is easy now, although it's really heavy, so you'll probably just put it back down right away.
By this point, most of the major oceans have become disconnected and stopped draining. The exact locations and sizes of the various inland seas are hard to predict; this is only a rough estimate.
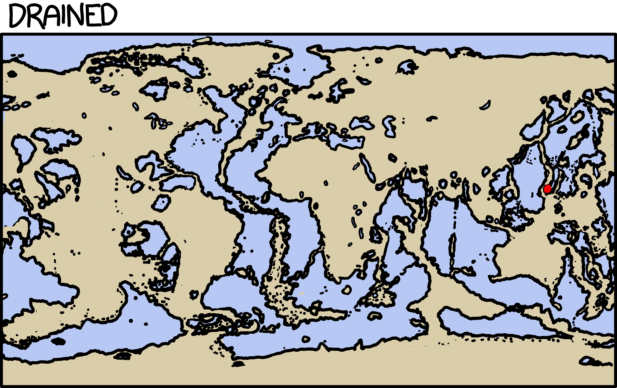
The deepest ocean on Earth is probably now the Northwest Atlantic, at the Milwaukee Deep in the Puerto Rico Trench. At this point, the water is still about four kilometers deep (half its original depth.)
This is what the map looks like when the drain finally empties. There's a surprising amount of water left, although much of it consists of very shallow seas, with a few trenches where the water is as deep as four or five kilometers.
Vacuuming up half the oceans would massively alter the climate and ecosystems in ways that are hard to predict. At the very least, it would almost certainly involve a collapse of the biosphere and mass extinctions at every level.
But it's possible—if unlikely—that humans could manage to survive. If we did, we'd have this to look forward to:
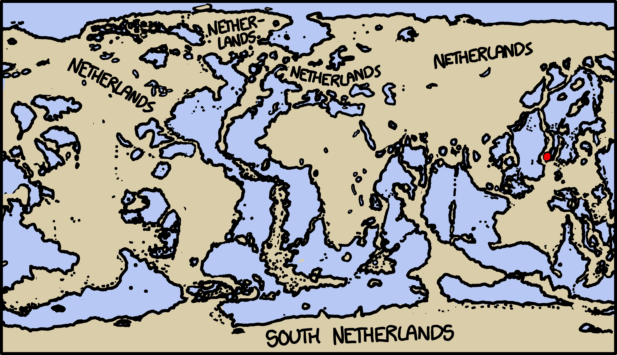
Maybe we shouldn't have drained the oceans.
we stole cheese, bought bread, baked pumkin, made salads, crushed almonds and wet you sister's bed
Supposing you did Drain the Oceans, and dumped the water on top of the Curiosity rover, how would Mars change as the water accumulated?
–Iain
In the previous What If, we opened a portal at the bottom of the Mariana Trench and let the oceans drain out.
We didn't worry too much about where the oceans were draining to. I picked Mars; the Curiosity rover is working so hard to find evidence of water, so I figured we could make things easier for it.

Instead of being sad forever, like Spirit, here's a rover that's briefly very happy!
Curiosity is sitting in Gale Crater, a round depression in the Martian surface with a peak, nicknamed Mt. Sharp, in the center.
There's a lot of water on Mars.[Donald Rapp, Accessible Water on Mars, JPL D-31343-Rev.7] The problem is, it's frozen. Liquid water doesn't last long there, because it's too cold and there's too little air.
If you set out a cup of warm water on Mars, it'll try to boil, freeze, and sublimate, practically all at once.[D. L. Santiago et. al., Mars climate and outflow events] Water on Mars seems to want to be in any state except liquid.
However, we're dumping a lot of water very fast (all of it at a few degrees above 0°C), and it won't have much time to freeze, boil, or sublimate. If our portal is big enough, the water will start to turn Gale Crater into a lake, just like it would on Earth. We can use the excellent USGS Mars Topographic Map to chart the water's progress.
Here's Gale Crater at the start of our experiment:
'Gale Lake' is a little awkward; I suggest 'Lake Gale'.
As the flow continues, the lake fills in, burying Curiosity under hundreds of meters of water:
What do I have against Curiosity? Well, I'm working for the Cat.
Eventually, Mt. Sharp becomes an island. However, before the peak can disappear completely, the water spills over the north rim of the crater and starts flowing out across the sand.
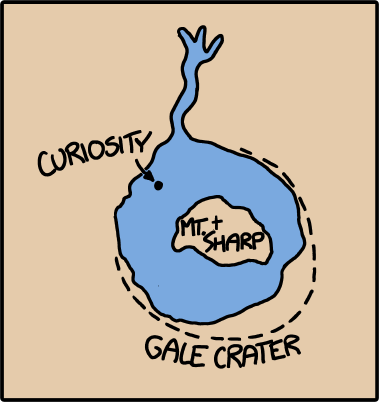
The stream flows north because of ... let's say 'the Coriolis Effect', and make some physics professor somewhere spit out their coffee.
When this kind of thing happens on Mars in real life, the trickle of water quickly dries up before it can get very far.[D. L. Santiago et. al., Cloud formation and water transport on mars after major outflow events, 43rd Planetary Science Conference (2012)] However, we've got a lot of ocean at our disposal.
The hand of Earth stretches across the desert.
The water pools in the North Polar Basin:
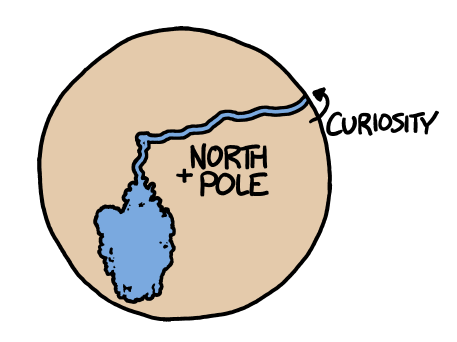
The defunct Phoenix lander is probably the first to go after Curiosity.
Gradually, it will fill the basin:
Then Viking.
However, if we look at a map of the more equatorial regions of Mars, where the volcanoes are, we'll see that there's still a lot of land far from the water:
![[Mercator projection; does not show the poles.]](imgs/a/54/mars_7.png)
[Mercator projection; does not show the poles.]
Frankly, I think this map is kind of boring; there's not a lot going on. It's just a big empty swath of land with some ocean at the top.
Would not buy again.
We haven't come close to running out of ocean yet. Although there was a lot of blue on the map of the Earth at the end of our last article, the seas that remained were shallow; most of the volume of the oceans was gone.
And Mars is much smaller than Earth, so the same volume of water will make a deeper sea.
At this point, the water fills in the Valles Marineris, creating some unusual coastlines. The map is less boring, but the terrain around the great canyons makes for some odd shapes.
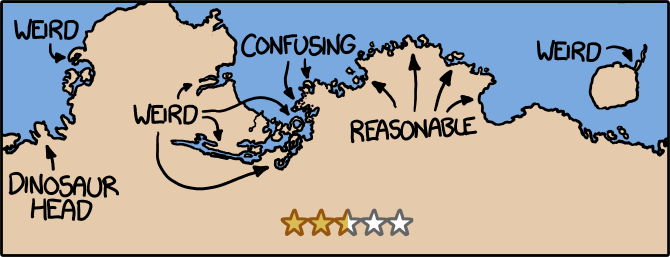
Instead of Earth ocean, portal disgorged bobcat. Would not buy again.
The water now reaches and swallows up Spirit and Opportunity. Eventually, it breaks into the Hellas Impact Crater, the basin containing the lowest point on Mars.
In my opinion, the rest of the map is starting to look pretty good.
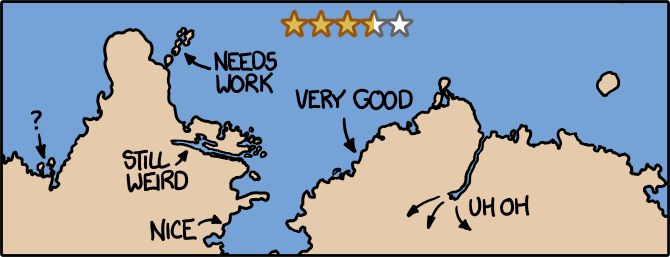
It's not the water's fault; the Valles Marineris are weird-looking in real life.
As the water spreads across the surface in earnest, the map splits into several large islands (and innumerable smaller ones).
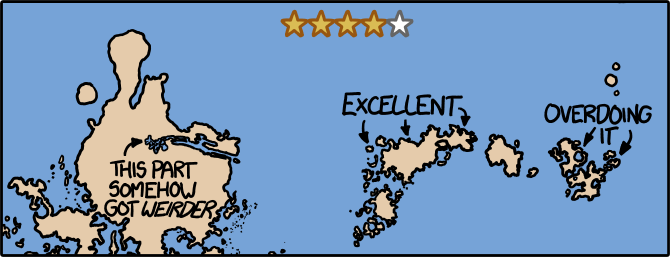
This looks like the map for a game where I would ignore the objectives and just sail around.
The water quickly finishes covering most of the high plateaus, leaving only a few islands left.

Zoom in. Enhance.
And then, at last, the flow stops; the oceans back on Earth are drained.
Let's take a closer look at the main islands:
No rovers remain above water.
Olympus Mons, and a few other volcanoes, remain above water. Surprisingly, they aren't even close to being covered. Olympus Mons still rises well over 10 kilometers above the new sea level. Mars has some huge mountains.
Those crazy islands are the result of water filling in 'Noctis Labyrinthus' ('the Labyrinth of the Night'), a bizarre set of canyons whose origin is still a mystery.
The oceans on Mars wouldn't last. There might be some transient greenhouse warming, but in the end, Mars is just too cold. Eventually, the oceans will freeze over, become covered with dust, and gradually migrate to the permafrost at the poles.[Maggie Fox, Mars May Not Have Been Warm Or Wet]
However, it would take a long time, and until it did, Mars would be a much more interesting place.
When you consider that there's a ready-made portal system to allow transit between the two planets, the consequences are inevitable:

Newtherlands.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
If you call a random phone number and say “God bless you”, what are the chances that the person who answers just sneezed? On average, not just in spring or fall.
–Mimi
It's hard to find good figures, but it's probably about 1 in 40,000.

Mimi is the more mannerly sister of Samara from The Ring.
Before you pick up the phone, you should also keep in mind that there's roughly a 1 in 1,000,000,000 chance that the person you're calling just murdered someone.[Based on a murder rate of 4 per 100,000, the average in the US but on the high end for industrialized countries.] You may want to be careful when you hand out blessings.
However, given that sneezes are far more common than murders,[Citation: You are alive.] you're still much more likely to get someone who sneezed than to catch a killer, so this strategy is not recommended:

Well, it's true.
(Mental note: I'm going to start saying that when people sneeze.)
Compared with the murder rate, the sneezing rate doesn't get much scholarly research. The most widely-cited figure for average sneeze frequency comes from a doctor interviewed by ABC News, who pegged it at 200 sneezes per person per year.[Cari Nierenberg, The Perils of Sneezing, ABC News, Dec. 22, 2008]
One of the few scholarly sources of data is a study which monitored the sneezing of people undergoing an induced allergic reaction.[Werner E. Bischoff, Michelle L. Wallis, Brian K. Tucker, Beth A. Reboussin, Michael A. Pfaller, Frederick G. Hayden, and Robert J. Sherertz, “Gesundheit!” Sneezing, Common Colds, Allergies, and Staphylococcus aureus Dispersion, J Infect Dis. (2006) 194 (8): 1119-1126 doi:10.1086/507908] To estimate the average sneezing rate, we can ignore all the real medical data they were trying to gather and just look at their control group. This group was given no allergens at all; they just sat alone in a room for a total of 176 20-minute sessions.[For context, that's 490 repititions of the song Hey Jude.]
The subjects in the control group sneezed four times during those 58 or so hours,[Over 58 hours of research, four sneezes were the most interesting data points. I might've taken the 490 Hey Judes.] which—assuming they only sneeze while awake—translates to about 400 sneezes per person per year.
Google Scholar turns up 5,980 articles from 2012 that mention "sneezing".[Google Scholar search for "sneezing"] If half of these articles are from the US, and each one has an average of four authors, then if you dial the number, there's about a 1 in 10,000,000 chance that you'll get someone who just that day published an article on sneezing.
On the other hand, about 60 people are killed by lightning in the US every year.[Lightning fatalities by country] That means there's only a 1 in 10,000,000,000,000 chance that you'll call someone in the 30 seconds after they've been struck and killed.
Your request for blessings has been preemptively denied.
Lastly, let's suppose that, on the day this article was published, five people who read it decide to actually try this experiment. If they call numbers all day, there's about a 1 in 30,000 chance that at some point during the day, one of them will get a busy signal because the person they've called is, themselves, calling a random stranger to say "God bless you."
And there's about a 1 in 10,000,000,000,000 chance that two of them will simultaneously call each other.

This is actually less likely than getting a murderer within 30 seconds of a murder.
At this point, probability will give up, and they'll both be struck by lightning.
we walked and talked, dreamt and got repelled by the shittiness of the world through documentaries
If you wanted to anchor an airplane into the ground so it wouldn't be able to take off, what would the rope have to be made out of?
—Connor Childerhose
Ah, the Just Cause 2 scenario.
At takeoff, a 747's four engines can each generate 281.57 kN of thrust. I have no real sense for what that number means, so let's put it in different terms:

Now, you put this whole contraption on a treadmill ...
A 747 with all engines at full could roughly balance the weight of a dangling blue whale.
With all that weight, how thick would the cable need to be?
Surprisingly, not all that thick! A cable a little over an inch in diameter would do it.[Bethlehem Wire Rope General Purpose Catalog]
Let's suppose you don't have a cable lying around. What else could you use?
If you're into fishing, you might have some fishing line. A typical line for saltwater fishing might have a 50-100 lb strength,[West Marine: Selecting Fishing Line] so it would take a brigade of several thousand people armed with fishing rods to restrain the plane.

Oh yeah? Well, the one *I* almost caught once was even bigger, and made out of wood! I swear it was real!
If you don't have fishing line, there's one thing you probably do have: Hair.
While hair isn't as strong as steel, it's just about the strongest material in your body,[Examples of the Tensile Strength of Materials] with a tensile strength rivaling or exceeding that of bone.[Properties of Textile Fibers]
This tensile strength is why performers are able to hang by their hair at the circus. In fact, from a materials standpoint, it's actually more impressive that performers are able to hang by their arms.
Based on these hair strength figures, a piece of hair three inches in diameter would be strong enough to restrain a 747.[If you wanted to measure the strength of a strand of hair, you could use the device described by US Patent #4628742A, "Tensile strength tester for hair" ]
Hairs that big around are hard to come by.[... I hope.] Since most of us have many small hairs, instead of one big hair ...
Why does nobody want to hang out with me??
... we'd need to get a lot of hairs and bundle them together. Given that individual hairs can support about 50 grams of weight, we'd need roughly 20 heads of hair to restrain the aircraft.

Hair Force One
Conclusion: Restraining a plane with a cable would be pretty easy.
Further conclusion: Blue whales are not typically covered in hair,[Although they are mammals, most whales do not have coats of hair like land mammals typically do] but if we transplanted the hair from at least 20 human heads onto a blue whale ...

I hope that answers your question.
... it would have enough hair to perform acrobatics at a circus.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
What if a huge mountain—Denali, say—had the bottom inch of its base disappear? What would happen from the impact of the mountain falling 1 inch? What about 1 foot? What if the mountain's base were raised to the present height of the summit, and then the whole thing were allowed to drop to the earth?
John-Clark Levin
The one-inch gap would take about 70 milliseconds to close. Don't stick your hand in.
If you want to learn more about what this would do to John-Clark's hand, you're welcome to search Google for industrial accident photos; I'm sure as hell not going to go looking for them.
The impact could trigger an earthquake. Denali (also known as Mount McKinley) is a mountain in Alaska that sits just to the south of a major fault line.[Roger A. Hansen, Earthquake and Seismic Monitoring in Denali National Park, National Park Service] This fault is active,[[Alaska Earthquake Information Center, M 7.9 Denali Fault earthquake of November 3, 2002]] and we know that drilling can trigger earthquakes.[Van der elst NJ, Savage HM, Keranen KM, Abers GA. Enhanced remote earthquake triggering at fluid-injection sites in the midwestern United States. Science. 2013;341(6142):164-7.] Earthquakes can happen at any time, so there's always a chance that dropping a mountain any distance could trigger one. So could kicking a tree. The only way to find out for sure would be to try it.[This article has an awful lot of citations.]
Assuming it didn't trigger an earthquake, the impact wouldn't be all that dramatic. If you were standing on the mountain when it happened, you'd definitely feel a jolt, but it probably wouldn't even be enough to knock you down.

I guess I was expecting ... I don't know what. But no, it was fine.
When the mountain hit the ground, the rock under it would be damaged, but only a little. The granite base is strong enough to hold up under the tremendous resting weight of a mountain;[Citation: The rock was holding up a mountain when you got there.] the shockwave from dropping it an inch doesn't add too much pressure on top of that, and the rock would survive with a little minor cracking.
People nearby would definitely feel the impact, and probably hear it; the sound would likely resemble the crack of a lightning strike (if you were standing near the mountain) fading into a long, deep rumble.[Citation: A dream I had once.] The vibration would be equivalent to that of a 3.5-magnitude earthquake[For more on the specific seismic details, see Stein, Seth, and Michael Wysession. "Earthquakes." An Introduction to Seismology, Earthquakes, and Earth Structure. Malden, MA: Blackwell Pub., 2003. 241. Print.]; at worst, it would knock a few pictures off the wall if you happened to be living next to the mountain. Frankly, I'd be more worried about debris flying out of the gap.[If your magical mountain-cutter put air in the space where the rock used to be, you should avoid standing near the crack when it falls. The air will come jetting out from the closing crack, spraying rocks and dust at speeds approaching, or even—thanks to some fun heat-related effects—exceeding, Mach 1.]

I see where this is going.
Oh. You again.
Ok.
Dropping from a height of one foot wouldn't be all that different.

What's that hissing sound?
The mountain would hit the ground at 2.5 m/s, or roughly walking speed. The shockwave from that impact would be in the range of 50 megapascals of pressure,[You can calculate the peak pressure of the compressive strain wave in the rock using the Joukowsky equation, which says that the peak pressure of the compressive wave in a material is (material's density)x(speed at impact)x(the speed of sound in the material). This equation is is normally used in fluid mechanics, but it works fine here, too!] which granite can handle without too much trouble.[Bhat HS, Sammis CG, Rosakis AJ. The Micromechanics of Westerley Granite at Large Compressive Loads. Pure Appl. Geophys. 2011;168(12):2181-2198.] ["... for a plane shock wave ... granite will stand a compressive stress of 3000-4000 MPa elastically before failing." Persson, Per-Anders, Roger Holmberg, and Jaimin Lee. Rock Blasting and Explosives Engineering. Boca Raton, FL: CRC, 1994. 5-6. Print.]

Ok. Let's jump straight to the end of John-Clark's question:

What, this mountain? It was hovering several miles above the Earth when we got here.
After falling from summit height to base height—about 5 kilometers—the mountain would be moving at roughly the speed of sound.
The last two impacts were pretty minor. This one wouldn't be. The jolt to the ground would be as violent as in a magnitude 7 earthquake.[In addition, there's a good chance that a shock this large will release some existing seismic energy; see: U.S. Congress, Office of Technology Assessment, Seismic Verification of Nuclear Testing Treaties, P. 715, OTA-ISC-361 (Washington, DC: U.S. Government Printing Office, May 1988).] There wouldn't exactly be a crater, but the mountain would definitely not be shaped like it used to be. The pressure from the impact would be high enough to produce some unusual geologic strutures. If you put a lump of coal under the meteor, the impact would be enough to convert it to diamond (and, unfortunately, smash it to bits).[French B. M. (1998) Traces of Catastrophe: A Handbook of Shock-Metamorphic Effects in Terrestrial Meteorite Impact Structures., Chapter 4, LPI Contribution No. 954,Lunar and Planetary Institute, Houston. 120 pp]
The good news is that, the last time a magnitude 7+ earthquake hit Denali, no one was killed.[[Alaska Earthquake Information Center, M 7.9 Denali Fault earthquake of November 3, 2002]] Let's just hope nobody is on the mountain itself when we do this.

Ok. Last one.
We'd need to lift the mountain out of the atmosphere, out past the orbit of the GPS satellites, to the very outer limits of the Earth's gravity well. Then we let go.

Sorry.
It would hit Alaska at 10 kilometers per second.
The Last Frontier would not fare well. A 50-mile-wide crater would have obliterated Denali National Park. Anchorage would be buried under three meters of gravel.[Purdue University ImpactEarth asteroid impact simulator] The shaking, combined with the debris falling into the ocean, would cause tsunamis across the Pacific. Across North America, the ground would tremble. A wind would sweep in from the northwest. The sky would darken.
In 1815, Mount Tambora erupted in the largest volcanic event in recorded history. The resulting global veil of aerosols made 1816 the "year without a summer". Snow fell in Massachusetts in June, ice formed on rivers in Pennsylvania in August, and frost killed most of the spring crops. The cooling effects lingered for several years.
The Alaska impact would be far worse. Over the next few months, the skies around the globe fill with dust. Summer is canceled and winter arrives. Global temperatures would drop by 5 to 20 degrees Celsius and stay that way for a year or more.[Covey, C, S Thompson, P Weissman, and M Maccracken. "Global Climatic Effects Of Atmospheric Dust From An Asteroid Or Comet Impact On Earth." Global and Planetary Change 9, no. 3-4 (1994): 263-273.]
On the plus side, we would not be engulfed in a global firestorm. When the Chicxulub comet hit the Yucatan peninsula 65 million years ago, it blasted molten debris into space. This debris fell back to Earth around the world, heating the atmosphere and igniting global firestorms. These may have played a role in the mass extinctions.[I don't have a citation for this. But, c'mon, it's a 'global firestorm'. Can you really imagine that every species made it through unscathed?]
However, our mountain would carry only about 10% of the energy of the Chicxulub impactor, which means that it wouldn't be capable of igniting global firestorms.[Osinski, G. R., and E. Pierazzo. "Environmental Effects of Impact Events." In Impact Cratering Processes and Products.. Chicester: Wiley, 2012. 151.] The firestorms would, in fact, only cover some of North America. So that's a relief.
The northern hemisphere would be covered in ice, but our species would probably manage to limp through. Civilization, on the other hand, might well collapse. A total collapse of modern civilization would be a serious blow to the already sluggish economy, and the economic damage could amount to $80 trillion per year (the total value of all human goods and services). All in all, it would have serious implications for the upcoming elections.
And that's that. We've dropped the mountain from as high as it can be dropped, and I hope John-Clark is proud of the resulting devastation. Thanks for reading, and—

No, that doesn't actually make sense. The Earth's gravitational pull doesn't—

Dropping it from higher up won't do anything; there won't be enough force pulling it toward the—

Ok. Fine. You win. We'll try it.
![I guess now Mount Logan is the tallest mountain in [the smoldering ruins of] North America.](imgs/a/57/mountain_higher.png)
I guess now Mount Logan is the tallest mountain in [the smoldering ruins of] North America.
Oops.
we wanted to be activists
What if a spacecraft slowed down on re-entry to just a few miles per hour using rocket boosters like the Mars-sky-crane? Would it negate the need for a heat shield?
—Brian
Is it possible for a spacecraft to control its reentry in such a way that it avoids the atmospheric compression and thus would not require the expensive (and relatively fragile) heat shield on the outside?
—Christopher Mallow
Could a (small) rocket (with payload) be lifted to a high point in the atmosphere where it would only need a small rocket to get to escape velocity?
—Kenny Van de Maele
The answers to these questions all hinge on the same idea. It's an idea I've touched on in other articles, but today I want to focus on it specifically:
The reason it's hard to get to orbit isn't that space is high up.
It's hard to get to orbit because you have to go so fast.
Space isn't like this:

Not actual size.
Space is like this:

You know what, sure, actual size.
Space is about 100 kilometers away. That's far away—I wouldn't want to climb a ladder to get there—but it isn't that far away. If you're in Sacramento, Seattle, Canberra, Kolkata, Hyderabad, Phnom Penh, Cairo, Beijing, central Japan, central Sri Lanka, or Portland, space is closer than the sea.
Getting to space[Specifically, low Earth orbit, which is where the International Space Station is and where the shuttles could go.] is easy. It's not, like, something you could do in your car, but it's not a huge challenge. You could get a person to space with a small sounding rocket the size of a telephone pole. The X-15 aircraft reached space[The X-15 reached 100 km on two occasions, both when flown by Joe Walker. ] just by going fast and then steering up.[Make sure to remember to steer up and not down, or you will have a bad time.]

You will go to space today, and then you will quickly come back.
But getting to space is easy. The problem is staying there.
Gravity in low Earth orbit is almost as strong as gravity on the surface. The Space Station hasn't escaped Earth's gravity at all; it's experiencing about 90% the pull that we feel on the surface.
To avoid falling back into the atmosphere, you have to go sideways really, really fast.
The speed you need to stay in orbit is about 8 kilometers per second.[It's a little less if you're in the higher region of low Earth orbit.] Only a fraction of a rocket's energy is used to lift up out of the atmosphere; the vast majority of it is used to gain orbital (sideways) speed.
This leads us to the central problem of getting into orbit: Reaching orbital speed takes much more fuel than reaching orbital height. Getting a ship up to 8 km/s takes a lot of booster rockets. Reaching orbital speed is hard enough; reaching to orbital speed while carrying enough fuel to slow back down would be completely impractical.[This exponential increase is the central problem of rocketry: The fuel required to increase your speed by one km/s multiplies your weight by about 1.4. To get into orbit, you need to increase your speed to 8 km/s, which means you'll need a lot of fuel: $ 1.4\times1.4\times1.4\times1.4\times1.4\times1.4\times1.4\times1.4\approx 15$ times the original weight of your ship.
Using a rocket to slow down carries the same problem: Every 1 km/s decrease in speed multiplies your starting mass by that same factor of 1.4. If you want to slow all the way down to zero—and drop gently into the atmosphere—the fuel requirements multiply your weight by 15 again. ]
These outrageous fuel requirements are why every spacecraft entering an atmosphere has braked using a heat shield instead of rockets—slamming into the air is the most practical way to slow down. (And to answer Brian's question, the Curiosity rover was no exception to this; although it used small rockets to hover when it was near the surface, it first used air-braking to shed the majority of its speed.)
How fast is 8 km/s, anyway?
I think the reason for a lot of confusion about these issues is that when astronauts are in orbit, it doesn't seem like they're moving that fast; they look like they're drifting slowly over a blue marble.
But 8 km/s is blisteringly fast. When you look at the sky near sunset, you can sometimes see the ISS go past ... and then, 90 minutes later, see it go past again.[There are some good apps and online tools to help you spot the station, along with other neat satellites. My favorite is ISS Detector, but if you Google you can find lots of others.] In those 90 minutes, it's circled the entire world.
The ISS moves so quickly that if you fired a rifle bullet from one end of a football field,[Either kind.] the International Space Station could cross the length of the field before the bullet traveled 10 yards.[This type of play is legal in Australian rules football.]
Let's imagine what it would look like if you were speed-walking across the Earth's surface at 8 km/s.
To get a better sense of the pace at which you're traveling, let's use the beat of a song to mark the passage of time.[Using song beats to help measure the passage of time is a technique also used in CPR training, where the song "Stayin' Alive" is used to .] suppose you started playing the 1988 song by The Proclaimers, I'm Gonna Be (500 Miles). That song is about 131.9 beats per minute, so imagine that with every beat of the song, you move forward more than two miles.
In the time it took to sing the first line of the chorus, you could walk from the Statue of Liberty all the way to the Bronx:
You'd be moving at about 15 subway stops per second.
It would take you about two lines of the chorus (16 beats of the song) to cross the English Channel between London and France.
The song's length leads to an odd coincidence. The interval between the start and the end of I'm Gonna Be is 3 minutes and 30 seconds,[Based on timing from the official Youtube video] and the ISS is moving is 7.66 km/s.
This means that if an astronaut on the ISS listens to I'm Gonna Be, in the time between the first beat of the song and the final lines ...

Just to burn up in the atmosphere above your door.
... they will have traveled just about exactly 1,000 miles.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
If you had a printed version of the whole of (say, the English) Wikipedia, how many printers would you need in order to keep up with the changes made to the live version?
Marein Könings
This many:

If a date took you home and you saw a row of working printers set up in their living room, what would you think?
That's surprisingly few printers! But before you try to create a live-updating paper Wikipedia, let's look at what those printers would be doing ... and how much they'd cost.
Printing Wikipedia
People have considered printing out Wikipedia before. A few years ago, student Rob Matthews printed every Wikipedia featured article, creating a book several feet thick.
Of course, that's just a small slice of the best of Wikipedia; the entire encyclopedia would be a lot bigger. Wikipedia user Tompw has set up a page for calculating the size of the whole English Wikipedia in printed volumes. It would currently fill a lot of bookshelves.
Keeping up with the edits would be harder.
Keeping up
The English Wikipedia currently receives about 125,000 to 150,000 edits each day, or 90-100 per minute.[ToolServer: Edit rate]
We could try to define a way to measure the "word count" of the average edit, but that's hard bordering on impossible. Fortunately, we don't need to—we can just estimate that each change is going to require us to reprint a page somewhere. Many edits will actually change multiple pages—but many other edits are reverts, which would let us put back pages we've already printed.[The filing system for this would be staggering.] One page per edit seems like a reasonable middle ground.
For a mix of photos, tables, and text typical of Wikipedia, a good inkjet printer might put out 15 pages per minute. That means you'd only need about six printers running at any given time to keep pace with the edits.
The paper would stack up quickly. Using Rob Matthews' book as a starting point, I did my own back-of-the-envelope estimate for the size of the current English Wikipedia. Based on the average length of featured articles vs. all articles, I came up with an estimate of 300 cubic meters for a printout of the whole thing.[That's a little larger than Tompw's estimate, but I'm assuming they're printed straight from the browser, which is less compact and includes images.]
By comparison, if you were trying to keep up with the edits, you'd print out 300 cubic meters every month.
$500,000 per month
Six printers isn't that many, but they'd be running all the time. And that gets expensive.
The electricity to run them would be cheap—a few dollars a day.
The paper would be about one cent per sheet, which means you'll be spending about a thousand dollars a day.
You'd want to hire people to manage the printers 24/7, but that would actually cost less than the paper.
Even the printers themselves wouldn't be too expensive, despite the terrifying replacement cycle.
But the ink cartridges would be a nightmare.
Ink
A study by QualityLogic[QualityLogic: Cost of Ink Per Page Analysis, June 2012] found that for a typical inkjet printer, the real-life cost of ink ran from 5 cents per page for black-and-white to around 30 cents per page for photos. That means you'd be spending four to five figures per day on ink cartridges.
You definitely want to invest in a laser printer. Otherwise, in just a month or two, this project could end up costing you half a million dollars:

No, it started long before that.
But that's not even the worst part.
If, someday, Wikipedia decides to go dark again, and you want to join the protest ...

Make sure not to remove all the marker caps at once and inhale deeply.
You'll have to get a crate of markers and color every page solid black yourself.
I would definitely stick to digital.
we wanted to spread happiness
If you could teleport to a random place of the surface of the Earth, what are the odds that you'll see signs of intelligent life?
Borislav Stanimirov
The surface of the Earth is about 70% water, so you'll usually plop down into the ocean.

Later, a shark bites the teleporter box and suddenly finds itself in the wave pool at a Texas water park.
But even there, you could find signs of human habitation.
But first, we'll start with ...
The big stuff
In one way or another, humans have altered every square meter of this planet. But we'll start with the obvious: Roads, houses, and fields.
To get an idea of how often Borislav would stumble across such obvious structures, I loaded up a sample of random geographic coordinates[Generating uniform points on a sphere is tricky—you can't just pick a random latitude and a random longitude. The solution is to either do a bunch of math or use something like GeoMidpoint's Random Point Generator.] in Google Earth.
Most of the points were over open ocean, out of sight of any land. Once you get away from the major ports, the odds of having a ship in view are not that good, so I continued sampling until I had 50 land coordinates.
Based on Google Earth imagery, Borislav would definitely see clear signs of human activity in about 10 of those 50 points. Six of them were actually in cultivated fields (in Poland, Argentina, Brazil, Pakistan, and Kazakhstan). Another point was in a highway cut along the coast of French Guiana. One was in a small town deep in the Amazon, and another on a road in the Australian outback.
In another five or ten cases, Borislav might be able to see something if you looked carefully or walked a short distance; it's hard to be sure without actually visiting the points to find out what you can see. Included in this list of marginal points was the only US location on the list, a spot in the woods outside in Keachi, Louisiana—a town which, during the American Civil War, saw the creation of a contingent of 'Highlanders' complete with government-issued kilts and plaids.
Most of the points were in the middle of deserts, barren mountains, tropical jungles. or—in one case—central Antarctica. All in all, it seems like the odds of landing somewhere with human artifacts in view are about one in four to one in three—and that artifact will usually be either a field of crops or a dirt road.
Look down
If you find yourself on a beach, check the sand. Sand all over the world contains tiny grains of plastic, mostly from industrial spillage into the oceans.[Patricia L. Corcorana, Mark C. Biesinger, Meriem Grifi, Plastics and beaches: A degrading relationship]. Even if you land in the water, you might still be able to spot bits of plastic debris; the ocean is covered with them, which leads to heartbreaking consequences.
Sample the air
If you have a CO2 meter—and you know Earth's atmospheric history—you can also detect the changes we've made to the air around you. Over the past hundred years, we've rapidly increased CO2 concentrations from less than 300 parts per million to over 400—higher than they've been in millions of years. It's not proof of technological activity, but it's a pretty good tip-off that something weird is going on.
More sensitive testing could detect human-generated aerosols, or—by testing the soils—detect the alterations we've made to the global nitrogen cycle.['Although carbon dioxide may get more press, “the nitrogen cycle has been altered more than any other basic element cycle,” says John Aber, vice president for research and public service at the University of New Hampshire.' Scott Fields, Global Nitrogen: Cycling out of Control]
Look up
Depending on the humidity, you may have a good chance of seeing jet contrails. Under the right conditions, these water vapor trails from planes can linger for hours. In many parts of the world, they're a common sight. However, in areas with fewer flight paths—central Africa, South America, and Australia, in particular—they might be less easy to spot.

But even if you find yourself in the middle of the Algerian desert, the Peruvian Amazon, or the Arctic cliffs of Transfiguration Island, there's an easy way to see evidence of intelligent life:
Wait for nightfall.[And then go crazy and burn down your civilization when you see the stars for the first time.]
At any given time, there are hundreds of satellites in the sky. Most of them are too faint to see, but if you're in an area without much light pollution, and you look carefully enough, there's virtually always a satellite visible. Their rapid motion across the sky and various highly inclined orbits make them unlikely to be anything but artificial.
It's often said that the Great Wall of China is the only human artifact that can be seen from space. This is wrong.
But in my opinion, the real problem with this factoid isn't that it's wrong—it's that it overlooks a much cooler point. The Great Wall of China may not be the only artifact on Earth that you can see from a satellite ... but our satellites are the only human artifacts that you can see from everywhere on Earth.
Want to see signs of intelligent life? Just look up.

You can't see the Great Wall of China from the space station ... but you can see the space station from the Great Wall of China. And that's pretty neat.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
How fast can you hit a speed bump while driving and live?
Myrlin Barber
Surprisingly fast.

Sorry, sir, the breathalyzer shows that you're above the legal limit for civic highway planning.
First, a disclaimer: After reading this article, don't try to drive over speed bumps at high speeds. Here are some reasons:
• You could hit and kill someone.
• It can destroy your tires, suspension, and potentially your entire car.
• Have you read any of the other articles on this blog?
If that's not enough, here are some quotes from medical journals on spinal injury from speed bumps:
Examination of the thoracolumbar X-ray and computed tomography displayed compression fractures in four patients ... Posterior instrumentation was applied ... All patients recovered well except for the one with cervical fracture.[Speed bump–induced spinal column injury]
L1 was the most frequently fractured vertebra (23/52, 44.2%)[Speed hump spine fractures: injury mechanism and case series]
Incorporation of the buttocks with realistic properties diminished the first vertical natural frequency from ~12 to 5.5 Hz, in agreement with the literature.[Source: The 2nd American Conference on Human Vibration.]
(That last one isn't directly related to speed bump injuries, but I wanted to include it anyway.)
Regular little speed bumps probably won't kill you
Speed bumps are designed to make drivers to slow down. Going over a typical speed bump at 5 miles per hour[Like anyone with a physics background, I do all my calculations in SI units, but I've gotten too many US speeding tickets to write this article in anything but miles per hour; it's just been burned into my brain. Sorry!] results in a gentle bounce, while hitting one at 20 delivers a sizable jolt. It's natural to assume that hitting a speed bump at 60 would deliver a proportionally larger jolt, but it probably wouldn't.
As those quotes attest, it's true that people are occasionally injured by speed bumps. However, nearly all of those injuries happen to a very specific category of people: Those sitting in hard seats in the backs of buses, riding on poorly-maintained roads.
When you're driving a car, the two main things protecting you from bumps in the road are the tires and the suspension. No matter how fast you hit a speed bump, unless the bump is particularly large, enough of the jolt will be absorbed by these two systems that you probably won't be hurt.
Absorbing the shock won't necessarily be good for those systems. In the case of the tires, they may absorb it by exploding.[Citation: Just Google "hit a curb at 60".] If the bump is large enough, it may permanently damage a lot of important parts of the car.
The typical speed bump is between three and four inches tall. That's also about how thick an average tire's cushion is (the separation between the bottom of the rims and the ground).[Citation: There are cars everywhere. Go outside with a ruler and check.] This means that if a car hits a small speed bump, the rim won't actually touch the bump; the tire will just be compressed.
The typical sedan has a top speed of around 120 miles per hour. Hitting a speed bump at that speed would, in one way or another, probably result in losing control of the car and crashing.[At high speeds, you can easily lose control even without hitting a bump. Joey Huneycutt's 220 mph crash left his Camaro a burned-out hulk.] However, the jolt itself probably wouldn't be fatal.
If you hit a larger speed bump—like a speed hump or speed table—your car might not fare so well.[Youtube: Speed bump in Dubai + flying Gallardo]
How fast would you have to go to definitely die?
Let's consider what would happen if a car went were going faster than its top speed.
The average modern car is limited to a top speed of around 120 mph, and the fastest can go about 200.[The Bentley Continental Flying Spur has a top speed of 199.64 miles per hour.]
While most passenger cars have some kind of artificial speed limits imposed by the engine computer, the ultimate physical limit to a car's top speed comes from air resistance. This type of drag increases up with the square of speed; at some point, a car doesn't have enough engine power to push through the air any faster.
If you did force a sedan to go faster than its top speed—perhaps by re-using the magical accelerator from the relativistic baseball—the speed bump would be the least of your problems.
Cars generate lift. The air flowing around a car exerts all kinds of forces on it.
Where did all these arrows come from?
The lift forces are relatively minor at normal highway speeds, but at higher speeds they become substantial.
In a Formula One car equipped with airfoils, this force pushes downward, holding the car against the track. In a sedan, they lift it up.[Parker, Barry R.. "Aerodynamic Design." In The Isaac Newton school of driving: physics and your car. Baltimore, MD: Johns Hopkins University Press, 2003. 155.]
Among NASCAR fans, there's frequently talk of a 200-mph "liftoff speed" if the car starts to spin.[The Myth of the 200-mph "Lift-Off Speed"] Other branches of auto racing have seen spectacular[Youtube: Porsche 911 GT2 (or GT1) crash] backflip crashes[Youtube: Mercedes CLR-GTR Le Mans Flip] when the aerodynamics don't work out as planned.
The bottom line is that at somewhere in the range of 150-300 mph, a typical sedan will lift off the ground, tumble, and crash ... before you even hit the speed bump.
BREAKING: Child, Unidentified Creature in Bicycle Basket Hit and Killed by Car
If you kept the car from taking off, the force of the wind at those speeds would strip away the the hood, side panels, and windows. At higher speeds, the car itself would be disassembled, or even burn up like a spacecraft reentering the atmosphere.
What's the ultimate limit?
In the state of Pennsylvania, drivers may have $2 added to their speeding ticket for every mile per hour by which they break the speed limit.[NHTSA, Summary of State Speed Laws, 2007]
Therefore, if you drove a car over a Philadelphia speed bump at 90% of the speed of light, in addition to destroying the city ...

It looks like debris from your car was seen violating the speed limit in 208 counties across 12 states.
... you could expect a speeding ticket of $1.14 billion.
we invited people for cake
What if I jumped out of an airplane with a couple of tanks of helium and one huge, un-inflated balloon? Then, while falling, I release the helium and fill the balloon. How long of a fall would I need in order for the balloon to slow me enough that I could land safely?
Colin Rowe
As ridiculous as it sounds, this is—sort of—possible.
Falling from great heights is dangerous.[citation needed] A balloon could actually help save you, although a regular helium one from a party obviously won't do the trick.
You were a poor choice for NTSB chairman.
If the balloon is large enough, you don't even need the helium. A balloon will act as a parachute, slowing your fall to non-fatal speeds.
Avoiding a high-speed landing is, unsurprisingly, the key to survival. As one medical paper[De Haven H. Mechanical analysis of survival in falls from heights of fifty to one hundred and fifty feet. Injury Prevention. 6(1):62-b-68.] put it,
It is, of course, obvious that speed, or height of fall, is not in itself injurious ... but a high rate of change of velocity, such as occurs after a 10 story fall onto concrete, is another matter.
... which is just a wordy version of the old saying, "It's not the fall that kills you, it's the sudden stop at the end."
To act as a parachute, a balloon filled with air, rather than helium, would have to be 10 to 20 meters across—far too big to be inflated with portable tanks. A powerful fan could be used to fill it with ambient air, but at that point, you may as well just use a parachute.
Helium
The helium makes things easier.
It doesn't take too many helium balloons to lift a person. In 1982, Larry Walters flew across Los Angeles in a lawn chair lifted by weather balloons, eventually reaching several miles in altitude. After passing through LAX airspace, he descended by shooting some of the balloons with a pellet gun.
On landing, Walters was arrested, although the authorities had some trouble figuring out what to charge him with. At the time, an FAA safety inspector told the New York Times, "We know he broke some part of the Federal Aviation Act, and as soon as we decide which part it is, some type of charge will be filed."[ARMCHAIR AIRMAN SAYS FLIGHT FULFILLED HIS LIFELONG DREAM, New York Times, July 4, 1982]
A relatively small helium balloon—certainly smaller than a parachute—will suffice slow your fall, but it still has to be huge by party balloon standards. The biggest consumer rental helium tanks are about 250 cubic feet, and you'd need to empty at least 10 of them to put enough air in the balloon to support your weight.
You'd have to do it quickly. The compressed helium cylinders are smooth and often quite heavy, which means they have a high terminal velocity. You'll only have a few minutes to use up all the cylinders. (As soon as you emptied one, you could drop it.)
You can't get around this problem by moving your starting point higher. Since the upper atmosphere is pretty thin, anything dropped from the stratosphere up will accelerate to very high speeds until it hits the lower atmosphere, then fall slowly the rest of the way. This is true of everything from small meteors[By the time meteors hit the Earth, they have slowed down to a few hundred miles per hour.] to Felix Baumgartner.[Jason Martinez, Falling Faster than the Speed of Sound, Wolfram Blog, October 24, 2012]

Fig. 2: AAAAAAAAAAAAAAA
But if you inflated the balloons quickly, possibly by connecting many canisters to it at once, you'd be able to slow your fall. Just don't use too much helium, or you'll end up floating at 16,000 feet like Larry Walters.

Click, then click and drag.
While researching this article,[Additionally, while researching impact speeds for this article, I came across a discussion on the Straight Dope Message Boards about survivable fall heights. One poster compared a fall from height to being hit by a bus. Another user, a medical examiner, replied that this was a bad comparison:
"When hit by a car, the vast majority of people are not run over; they are run under. The lower legs break, sending them into the air. They usually strike the hood of the car, often with the back of the head impacting the windshield, "starring" the windshield, possibly leaving a few hairs in the glass. They then go over the top of the car. They are still alive, although with broken legs, and maybe with head pain from the nonfatal windshield impact. They die when they hit the ground. They die from head injury."
The lesson: Don't mess with medical examiners. They're apparently pretty hardcore.] I managed to lock up my copy of Mathematica several times on balloon-related differential equations, and subsequently got my IP address banned from Wolfram|Alpha for making too many requests. The ban-appeal form asked me to explain what task I was performing that necessitated so many queries, so this is what I put:
Sorry, Wolfram.
I hope they understand.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
If all digital data were stored on punch cards, how big would Google's data warehouse be?
James Zetlen

In terms of storage capacity, a punch card is 0.57 tweets.
Google almost certainly has more data storage capacity than any other organization on Earth.
Google is very secretive about its operations, so it's hard to say for sure. There are only a handful of organizations who might plausibly have more storage capacity or a larger server infrastructure. Here's my short list of the top contenders:
Honorable mentions:
Let's take a closer look at Google's computing platform.
Follow the money
We'll start by following the money. Google's aggregate capital expenditures–spending on building stuff[I'm excluding the cost of an extremely expensive building they bought in New York.]—adds up to somewhere over $12 billion dollars.[Data Center Knowledge: Google’s Data Center Building Boom Continues: $1.6 Billion Investment in 3 Months] Their biggest data centers cost half a billion to a billion dollars, so they can't have more than 20 or so of those.
On their website,[Data center locations] Google acknowledges that they have datacenters in the following locations:
In addition, they appear to operate a number of other large datacenters (sometimes through subsidiary corporations), including:
They also operate equipment at dozens to hundreds of smaller locations around the world.
Follow the power
To figure out how many servers Google is running, we can look at their electricity consumption. Unfortunately, we can't just sneak up to a datacenter and read the meter.[Actually, wait, can we? Somebody should try that.] Instead, we have to do some digging.
The company disclosed that in 2010 they consumed an average of 258 megawatts of power.[Google used 2,259,998 MWh of electricity in 2010, which translates to an average of 258 megawatts.] How many computers can they run with that?
We know that their datacenters are quite efficient, only spending 10-20% of their power on cooling and other overhead.[Google: Efficiency: How we do it] To get an idea of how much power each server uses, we can look at their "container data center" concept from 2005. It's not clear whether they actually use these containers in practice—it may just have been a now-outdated experiment—but it gives an idea of what they consider(ed) reasonable power consumption. The answer: 215 watts per server.
Judging from that number, in 2010, they were operating around a million servers.
They've grown a lot since then. By the end of 2013, the total amount of money they've pumped into their datacenters will be three or four times what it was as of 2010. They've contracted to buy over three hundred megawatts of power at just three sites,[Google: Purchasing clean energy] which is more than they used for all their operations in 2010.
Based on datacenter power usage and spending estimates, my guess would be that Google is currently running—or will soon be running—between 1.8 and 2.4 million servers.
But what do these "servers" actually represent? Google could be experimenting in all kinds of wild ways, running boards with 100 cores or 100 attached disks. If we assume that each server has a couple[Anywhere from 2 to 5] of 2 TB disks attached, we come up with close to 10 exabytes[As a refresher, the order is: kilo, mega, giga, tera, peta, exa, zetta, yotta. An exabyte is a million terabytes.] of active storage attached to running clusters.
10 Exabytes
The commercial hard disk industry ships about 8 exabytes worth of drives annually.[IDC: Worldwide External Disk Storage Systems Factory Revenue Declines for the Second Consecutive Quarter] Those numbers don't necessarily include companies like Google, but in any case, it seems likely that Google is a large piece of the global hard drive market.
To make things worse, given the huge number of drives they manage, Google has a hard drive die every few minutes.[Eduardo Pinheiro, Wolf-Dietrich Weber and Luiz Andre Barroso, [Failure Trends in a Large Disk Drive Population] This isn't actually all that expensive a problem, in the grand scheme of things—they just get good at replacing drives—but it's weird to think that when a Googler runs a piece of code, they know that by the time it finishes executing, one of the machines it was running on will probably have suffered a drive failure.
Google tape storage
Of course, that only covers storage attached to running servers. What about "cold" storage? Who knows how much data Google—or anyone else—has stored in basement archives?
In a 2011 phone interview with Paul Mah of SMB Tech, Simon Anderson of Tandberg Data let slip[SMB Tech: Is Tape Still Relevant for SMBs?] that Google is the world's biggest single consumer of magnetic tape cartridges, purchasing 200,000 per year. Assuming they've stepped up their purchasing since then as they've expanded, this could add up to another few exabytes of tape archives.
Putting it all together
Let's assume Google has a storage capacity of 15 exabytes, or 15,000,000,000,000,000,000 bytes.
A punch card can hold about 80 characters, and a box of cards holds 2000 cards:

Four boxes of punch cards ought to be enough for anyone.
15 exabytes of punch cards would be enough to cover my home region, New England, to a depth of about 4.5 kilometers. That's three times deeper than the ice sheets that covered the region during the last advance of the glaciers:
Illustration courtesy xkcd.com, used with permission.
That seems like a lot.
However, it's nothing compared to the ridiculous claims by some news reports about the NSA datacenter in Utah.
NSA datacenter
The NSA is building a datacenter in Utah. Media reports claimed that it could hold up to a yottabyte of data,[CNET: NSA to store yottabytes in Utah data centre] which is patently absurd.
Later reports changed their minds, suggesting that the facility could only hold on the order of 3-12 exabytes.[Forbes: Blueprints Of NSA's Ridiculously Expensive Data Center In Utah Suggest It Holds Less Info Than Thought] We also know the facility uses about 65 megawatts of power,[Salt-Lake City Tribune: NSA Bluffdale Center won’t gobble up Utah’s power supply] which is about what a large Google datacenter consumes.
A few headlines, rather than going with one estimate or the other, announced that the facility could hold "between an exabyte and a yottabyte" of data[Dailykos: Utah Data Center stores data between 1 exabyte and 1 yottabyte] ... which is a little like saying "eyewitnesses report that the snake was between 1 millimeter and 1 kilometer long."
Uncovering further Google secrets
There are a lot of tricks for digging up information about Google's operations. Ironically, many of them involve using Google itself—from Googling for job postings in strange cities to using image search to find leaked cell camera photos of datacenter visits.
However, the best trick for locating secret Google facilities might be the one revealed by ex-Googler talentlessclown on reddit:[reddit: Can r/Australia help find Google's Sydney data center? Seems like a bit of a mystery...]
The easiest way to find manned Google data centres is to ask taxi drivers and pizza delivery people.
There's something pleasing about that. Google has created what might be the most sophisticated information-gathering apparatus in the history of the Earth ... and the only people with information about them are the pizza delivery drivers.
Who watches the watchers?

Quis mulgere ipsos lac homines?
Apparently, Domino's.
we got the community idea
If you suddenly began rising steadily at one foot per second, how exactly would you die? Would you freeze or suffocate first? Or something else?
Rebecca B.
Did you bring a coat?
A foot per second isn't that fast—it's substantially slower than a typical elevator.[Otis: About Elevators] It would take you 5-7 seconds to rise out of arms' reach, depending how tall your friends are.

No! It's time.
After 30 seconds, you'd be 30 feet—9 meters—off the ground. Judging from What-If #44, this is getting close to your last chance for a friend to throw you a sandwich or water bottle or something.[Not that it will help, ultimately.]

We've been standing here since that last article like five months ago. Why do you do this to us??
After a minute or two you would be above the trees. You'd still be about as comfortable as you were on the ground. If it's a breezy day, it will probably get chillier thanks to the steadier wind above the treeline.[For this article, I'm going to assume a typical atmosphere temperature profile. It can, of course, vary quite a bit.]
After 10 minutes you would be above all but the tallest skyscrapers, and after 25 minutes you'd pass the spire of the Empire State Building.
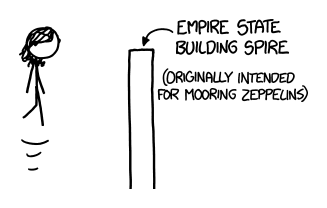
Every reminder of which breaks a thousand steampunk hearts.
The air at these heights is about 3% thinner than it is at the surface. Fortunately, your body handles air pressure changes like that all the time. Your ears may pop, but you wouldn't really notice anything else.
Air pressure changes quickly with height. Surprisingly, when you're standing on the ground, air pressure is even measurably lower at your head than at your feet. If your phone has a barometer in it, as a lot of new Android phones do, you can download an app and actually see the pressure difference between your head and your feet.
A foot per second is pretty close to a kilometer per hour, so after an hour, you'll be about a kilometer off the ground. At this point, you definitely start to get chilly. If you have a coat, you'll still be ok, though you might also notice the wind picking up.
At about two hours and two kilometers, the temperature would drop below freezing. The wind would also, most likely, be picking up. If you have any exposed skin, this is where frostbite starts to become a concern.[National Weather Service: Wind Chill Temperature Index]
Starting at this point, the air pressure would drop below what you'd experience in an airliner cabin,[... which are typically kept pressurized at about 70%-80% of sea level pressure, judging from the barometer in my phone.] and the effects would start to become more significant, but unless you had a warm coat, the temperature would be a bigger problem.
Over the next two hours, the air would drop to below-zero[Either unit.][Not Kelvin, though.] temperatures. Assuming for a moment that you survived the oxygen deprivation, at some point you'd freeze to death. But when?
The scholarly authorities on freezing to death seem to be, unsurprisingly, Canadians. The most widely-used model for human survival in cold air was developed by Peter Tikuisis and John Frim for the Defence and Civil Institute of Environmental Medicine in Ontario.[Prediction of Survival Time in Cold Air—see page 24 for the relevant tables.]
According to their model, the main factor in the cause of death would be your clothes. If you were nude, you'd probably succumb to hypothermia somewhere around the five hour mark, before your oxygen ran out.[And frankly, this really raises more questions than it answers.] If you were bundled up, you may be frostbitten, but you would probably survive ...
... long enough to reach the Death Zone.
It's not as bad as it sounds! ... that's a lie.
Above 8,000 meters—above the tops of all but the highest mountains—the oxygen content in the air is too low to support human life. Near this zone, you would experience a range of symptoms, possibly including confusion, dizziness, clumsiness, impaired vision, and nausea.
As you approach the Death Zone, your blood oxygen content would plummet. Your veins are supposed to bring low-oxygen blood back to your lungs to be refilled with oxygen. But in the Death Zone, there's so little oxygen in the air that your veins lose oxygen to the air instead of gaining it.[Linda D. Pendleton, When Humans Fly High: What Pilots Should Know About High-Altitude Physiology, Hypoxia, and Rapid Decompression]
The result would be a rapid loss of consciousness and death. This would happen around the seven hour mark; the chances are very slim that you would make it to eight.
She died as she lived—rising at a foot per second. I mean, as she lived for the last few hours.
And two million years later, your frozen body, still moving along steadily at a foot per second, would pass through the heliopause into interstellar space—the same boundary that Voyager just crossed.[Again.]
Clyde Tombaugh, the astronomer who discovered Pluto, died in 1997. A portion of his remains were placed on New Horizons spacecraft, which will fly past Pluto and then continue out of the Solar System.
It's true that your hypothetical foot-per-second trip would be cold, unpleasant, and rapidly fatal. But when the Sun becomes a red giant in four billion years and consumes the Earth, you and Clyde would be the only ones to escape.
So there's that.

So long, suckers!
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
If our Twitter timelines (tweets by the people we follow) actually extended off the screen in both directions, how tall would they be?
Anonymous

Wait, in pixels or points?
This is a surprisingly tricky question. The answer involves German tanks, human extinction, and the most disputed statistics problem on the internet.
But first, Twitter.
Lots of tweets
The answer obviously depends who you follow. Some people tweet a lot more than others.
@JephJacques, the author of Questionable Content, tweets a lot. His contribution to your timeline will be 36,000 tweets and rising. On the other hand, if you follow people who don't tweet very much, it's possible your timeline to date could fit on a single screen.
According to an analysis by Diego Basch, as of last year the "average" Twitter account had tweeted 307 times and was following 51 people.[Diego Basch, Some Fresh Twitter Stats (as of July 2012, Dataset Included) (Dataset not included.)] But averages can be deceptive;[If Larry Ellison, who made $96 million last year, moves into a typical town of 3,000 people, the average income in that town will double overnight.] most Twitter accounts had never even tweeted at all, or have only one follower.
To get an idea of the typical timeline, I asked some friends to take a snapshot of their Twitter homepages and count the rate of tweets at that particular moment. The results covered a wide range—some were seeing 20 tweets per minute, some 20 tweets per month.
Correcting[Multiplying by a random number between 0.5 and 1] for the time of day and extrapolating[Filling a spreadsheet with numbers until I ran out of columns] backward based on Twitter's growth rate, this suggested some timelines currently contain hundreds of tweets and some contain millions.
On my computer's monitor, the average tweet is about 2.4 centimeters high.[Citation: I just measured. You can measure, too, but you'll have to use your computer instead of mine. I'm using mine now to type this, so I need to be able to see the screen.] This suggests that Jeph Jacques' tweet tower is 900 meters tall—taller than the tallest building—and still growing.
However, Jeph has nothing on @YOUGAKUDAN_00, who tweets many times per minute—usually binary, but sometimes actual words. @YOUGAKUDAN_00 has accumulated 37 million tweets, enough to reach into low Earth orbit.
Combining Diego's July 2012 estimate with the current rate of tweets per day suggests there have been a total of about 345 billion tweets as of October 2013. That means that if you followed every Twitter user, your timeline would be eight million kilometers high. For comparison, here's the Earth, with your Twitter timeline next to it:

See this pale white line? That's Twitter. Every novelty account, every drunk tweet, every weird and/or racist hashtag...
Of course ... that's just the part of the timeline below the screen. What about the whole timeline?
A bug in the Twitter app briefly makes it so you can swipe down to refresh and see future tweets that haven't yet been posted.
Someday, the last person you follow will tweet for the last time. When will that be?
The future
Our timelines aren't really as tall as skyscrapers—even virtually–because Twitter limits the number of past tweets you can see by scrolling. But can we estimate how tall our timelines will eventually be?
Based on human lifespans, it seems likely that most of the accounts you follow will stop tweeting within a century. On the other hand, accounts like @big_ben_clock could keep going for millennia.
But will Twitter last that long?
It's obviously impossible to predict for sure, but there's a strange tool from statistics that might help.[Predict the end of Twitter with this 1 weird old tip!]
Or might not. It depends who you talk to.
German tank problem
Suppose you're transported to an alternate universe. You open IMDb and load a random page, and the movie that comes up is The Land Before Time XXVII.[27]
Based only on the title, how many Land Before Time movies do you think there are in this universe? Clearly there are at least [27], and probably more.
Allied troops faced a version of this problem in World War II.[(A flood of Axis-produced Land Before Time sequels.)] German tank parts had serial numbers, many of which were sequential (1, 2 ... N). Suppose they captured a random tank. If they determined it was Tank #[27], then they can be sure that the Germans had made at least [27] tanks. It also told them there probably weren't millions of tanks; if there were, they would have been unlikely to get a two-digit serial number.
Of course, the enemy can foil this plan by giving their tanks random large serial numbers. The US actually did that in 1981—the Navy named its elite counterterrorism unit "Seal Team Six" to confuse Soviet spies into thinking there must be at least five other teams out there.[Pfarrer, Chuck. "Team Jedi." In SEAL target Geronimo: the inside story of the mission to kill Osama Bin Laden. New York: St. Martin's Press, 2011. Loc 594/3898.]
Assuming the numbers are sequential, using clever Bayesian math, you can guess the actual number from a sample of tanks pretty reliably.[In addition to the Wikipedia article, there are good discussions of the solution on Statistics Blog and Event Horizon]
If you have only a few samples, the math gets a little trickier.[The problem is that you're forced to select a "prior"—an initial hypothesis about how likely each number of tanks is. Usually, people just assume there's an equal chance of every number of tanks. But mathematically, this assumption plays fast and loose with the math. The idea of having "an equal chance of getting every number from 1 to infinity" doesn't work in probability; technically speaking, it violates Kolmogorov's Second Axiom. ] With one sample—as in our Land Before Time problem—the best strategy is probably to take the number you've seen and double it. This suggests that there are probably about 54 Land Before Time Movies.
The idea is that you're likely to be somewhere in the middle of the range—there's only a small chance that you're looking at one of the first or one of the last movies.
Things get weird
If we apply the German tank problem to humans, we can argue that our species will go extinct by the year 2807.
Here's the argument:
Humans will go extinct someday. Suppose that, after this happens, aliens somehow revive all humans who have ever lived. They line us up in order of birth and number us from 1 to N. Then they divide us divide them into three groups—the first 5%, the middle 90%, and the last 5%:

Why are you doing this?
Now imagine the aliens ask each human (who doesn't know how many people lived after their time), "Which group do you think you're in?"
Most of them probably wouldn't speak English, and those who did would probably have an awful lot of questions of their own. But if for some reason every human answered "I'm in the middle group", 90% of them will (obviously) be right. This is true no matter how big N is.
Therefore, the argument goes, we should assume we're in the middle 90% of humans. Given that there have been a little over 100 billion humans so far, we should be able to assume with 95% probability that N is less than 2.2 trillion humans. If it's not, it means we're assuming we're in 5% of humans—and if all humans made that assumption, most of them would be wrong.
To put it more simply: Out of all people who will ever live, we should probably assume we're somewhere in the middle; after all, most people are.
If our population levels out around 9 billion, this suggests humans will probably go extinct in about 800 years, and not more than 16,000.
This is the Doomsday Argument.
Yeah, but that's stupid
Almost everyone who hears this argument immediately sees something wrong with it.
The problem is, everyone thinks it's wrong for a different reason. And the more they study it, the more they tend to change their minds about what that reason is.
Since it was proposed in 1983, it's been the subject of tons of papers refuting it, and tons of papers refuting those papers.[Nick Bostrom, A Primer on the Doomsday Argument] There's no consensus about the answer; it's like the airplane on a treadmill problem, but worse.
What does this mean for Twitter?
Let's assume the Doomsday argument is valid and apply this reasoning to Twitter. Since there have been 345 billion tweets so far, then the best guess about Twitter's total lifetime is that there will be 690 billion tweets.
At the current rate of 400 million tweets per day, this argument says Twitter has about five years left. And it suggests that there's a 95% chance Twitter will disappear within 45 years.
This certainly sounds reasonable—given the rate of technological change, there's no reason to expect an internet service to stay popular for more than 10 or 20 years.
But ... is the Doomsday argument valid?

Option three is obviously correct.
If we see Twitter activity winding down in 2018, then will that be evidence in favor of the Doomsday argument? And if so, does it suggest that humanity has only two centuries left?
Probably not. But it depends which statisticians you ask.
On the plus side, they seem to have stopped making The Land Before Time sequels in 2007, so at least we stand a good chance of avoiding that particular scenario.
Tommy Wiseau's 'The Land Before Time XX' is widely regarded as the worst in the series.
i like you
If winds reached 500 mph, would it pick up a human?
Grey Flynn, age 7, Stoneham, MA
Absolutely!
Grey Flynn, age 7, rapidly exiting Stoneham, MA.
Some things don't work like they do in the movies. Getting shot doesn't really make someone fly backward. The vacuum of space doesn't make your skin explode.
But high wind can definitely pick up a person. In fact, if you were standing in the parking lot, the wind wouldn't just pick you up—it would also peel the pavement from the ground!
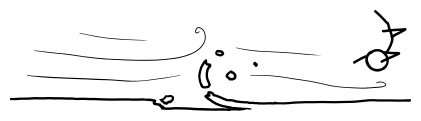
The strongest tornadoes often peel up pavement.
It wouldn't be strong enough to peel your skin off. Humans can survive blasts of 500 mph wind, which is important because pilots sometimes need to eject from airplanes at those speeds.
In the 1940s, the US government put pilots in wind tunnels to learn how they reacted to high winds. Have you ever been curious what happens to a person's face in 457 mph winds? Well, you can watch a video of one of those wind tunnel tests here. (That test was conducted at NASA Langley Research Center, where I worked before I started drawing internet comics for a living.)
It doesn't look very comfortable—I didn't know cheeks could flap like that—but the pilot appears to stay alive.
Luckily, he's strapped into that chair. He wouldn't be able to stand up in those winds! If he tried, he would go flying backward down the tunnel.
High wind is really powerful. In a paper in the journal Weather, J. F. R. McIlveen showed how to calculate the force of wind on the human body.[McIlveen, J. F. R.. "The Everyday Effects Of Wind Drag On People." Weather 57, no. 11 (2002): 410-413.] The calculations on page 2 show how far you'd have to lean to stay upright in wind of various speeds.
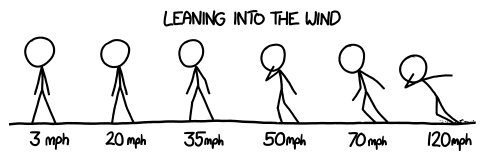
I carry this chart around so if I get hit by a tornado, I'll know how far to lean.
When wind speed rises above about 120 mph, it's no longer possible to stay upright no matter how far you lean; you'll start to slide backward across the ground,[When Hurricane Isabel hit Virginia in 2003, I had the bright idea of standing on a skateboard with a poncho held up like a sail, so the wind would blow me down the street. But the moment I got the sail up, the wind fell quiet.
Later, I learned that people die from doing that. Oops.] then quickly go head over heels and start to tumble.
You wouldn't necessarily be thrown very high. If the wind were perfectly level, you'd tumble along the surface, bouncing against the ground. However, if there were any updrafts, you could easily be lifted up and carried away.
The good news is that 500 mph winds are rare. The strongest hurricanes have wind speeds around 200 mph with gusts up to 250.[Courtney, J.; Buchan, S.; Cerveny, R.S.; Bessemoulin, P.; Peterson, T.C.; Rubiera Torres, J.M.; Beven, J.; King, J.; Trerwin, B.; Rancourt, K.. 2012 "Documentation and verification of the world extreme wind gust record: 113.3 m s–1 on Barrow Island, Australia, during passage of tropical cyclone Olivia." Australian Meterological and Oceanographic Journal, 62 (1). 1-9.] Tornadoes can reach 300 mph.[It's difficult to get accurate measurements of surface winds since those tornadoes destroy most measuring equipment!] 300 is a far cry from 500; the force from a 500 mph wind is several times stronger than the force from a 300 mph wind.
There are a few ways you could experience wind speeds faster than 500 mph. One is to stand on top of a volcano when it erupts. When Mount St. Helens exploded in 1980, the column of ash was blasted outward at 700 mph, which is close to the speed of sound.[Kieffer, S. W., 1981, Fluid dynamics of the May 18 blast at Mount St. Helens, in Lipman, P.W., and Mullineux, D.R., eds., The 1980 Eruptions of Mount St. Helens, Washington: U.S. Geological Survey Professional Paper 1250, p. 379-400.]
Another way to experience 500 mph winds is to trigger a hypercane.[Limits on Hurricane Intensity] A hypercane is an exotic type of hurricane with 500 mph winds spinning in a very tight vortex just a few miles across.
Hypercanes can't exist on Earth right now. To form, they require ocean temperatures of about 50°C. No matter how much we warm the planet, we're not going to get the temperature that high any time soon.
However, there's one way these storms might happen.
When an asteroid or comet—coincidentally, one about the size of the recently-named 4942 Munroe—hit Mexico 65 million years ago, it punched a hole in the crust and left behind a sea of lava.[Christeson, Gail L., Gareth S. Collins, Joanna V. Morgan, Sean P.S. Gulick, Penny J. Barton, and Michael R. Warner. "Mantle Deformation Beneath The Chicxulub Impact Crater." Earth and Planetary Science Letters 284, no. 1-2 (2009): 249-257.] When water flowed back in to fill the hole, it would have been heated by contact with the molten rock. This might have created the conditions for hypercanes to form, and one paper suggests that these storms could have lifted a large amount of dust and debris into the upper atmosphere—thus contributing to a global winter and extinction of the dinosaurs.[Emanuel, Kerry A., Kevin Speer, Richard Rotunno, Ramesh Srivastava, and Mario Molina. "Hypercanes: A Possible Link In Global Extinction Scenarios." Journal of Geophysical Research 100, no. D7 (1995): 13755-13765.]
It's just awesome enough to work.
In short, the answer to Grey's question is yes—500 mph winds would send you flying through the air. But don't worry about that. Instead, worry about is the thing that created the 500 mph winds. Odds are, that's what's going to kill you.

I'm working on figuring out a way to make this happen.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
How long would it take for people to notice their weight gain if the mean radius of the world expanded by 1cm every second? (Assuming the average composition of rock were maintained.)
Dennis O'Donnell
The Earth is not, currently, expanding.[Yes, I have a citation for this.
"In conclusion, no statistically significant present expansion rate is detected by our study within the current measurement uncertainty of 0.2 mm yr−1."
Wu, X., X. Collilieux, Z. Altamimi, B. L. A. Vermeersen, R. S. Gross, and I. Fukumori (2011), Accuracy of the International Terrestrial Reference Frame origin and Earth expansion, Geophys. Res. Lett., 38, L13304, doi:10.1029/2011GL047450.]
People have long suggested that it might be. Before the continential drift hypothesis was confirmed in the 1960s,[The smoking gun that confirmed the plate tectonics hypothesis was the discovery of seafloor spreading. The way seafloor spreading and magnetic pole reversal neatly confirmed each other is one of my favorite examples of scientific discovery at work.] people had noticed that the continents fit together. Various ideas were put forward to explain this, including the idea that the ocean basins were rifts that opened in the surface of a previously-smooth Earth as it expanded. This theory was never very widespread,[It turns out it's kind of dumb.] although it still periodically makes the rounds on YouTube.
To avoid the problem of rifts in the ground, let's imagine all the matter in the Earth, from the crust to the core, starts expanding uniformly. To avoid another Drain the Oceans scenario, we'll assume the ocean expands, too.[As it turns out, the ocean is expanding, since it's getting warmer. This is (currently) the main way global warming is raising the sea level.] All human structures will stay.
t = 1 second:

Oh, ok.
As the Earth started expanding, you'd feel a slight jolt, and might even lose your balance for a moment. This would be very brief. Since you're moving steadily upward at 1 cm/s, you woudn't feel any kind of ongoing acceleration. For the rest of the day, you wouldn't notice much of anything.
t = 1 day:
After the first day, the Earth would have expanded by 864 meters.
Let's go ride bikes!
Gravity would take a long time to increase. If you weighed 70 kilograms when the expansion started, you'd weigh 70.01 at the end of the day.
What about our roads and bridges? Eventually, they would have to break up, right?
Not as quickly as you might think. Here's a puzzle I once heard:
Imagine you tied a rope tightly around the Earth, so it was hugging the surface all the way around.
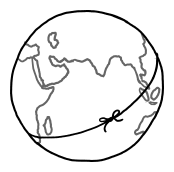
This diagram taken from some ambitious Ikea assembly instructions.
Now imagine you wanted to raise the rope one meter off the ground.

This chair doesn't look right.
How much extra length will you need to add to the rope?
Though it may seem like you'd need miles of rope, the answer is 6.28 meters. Circumference is proportional to radius, so if you increase radius by 1 unit, you increase circumference by 2π units.
Stretching a 40,000-kilometer line an extra 6.28 meters is pretty negligible. Even after a day, the extra 5.4 kilometers would be handled easily by virtually all structures. Concrete expands and contracts by more than that every day.[Lawrence Grybosky, Thermal Expansion and Contraction]
After the initial jolt, one of the first effects you'd notice would be that your GPS would stop working. The satellites would stay in roughly the same orbits, but the delicate timing that the GPS system is based on would be completely ruined within hours. GPS timing is incredibly precise; of all the problems in engineering, it's one of the only ones in which engineers have been forced to include both special and general relativity in their calculations.
Most other clocks would keep working fine. However, if you have a very precise pendulum clock, you might notice something odd—by the end of the day, it would be three seconds ahead of where it should be.
t = 1 month:
After a month, the Earth would have expanded by 26 kilometers—an increase of 0.4%—and its mass would have increased by 1.2%. Surface gravity would only have gone up by 0.4%, rather than 1.2%, since surface gravity is proportional to radius.[Mass is proportional to radius cubed, and gravity is proportional to mass times inverse square of radius, so radius3 / radius2 = radius.]
You might notice the difference in weight on a scale, but it's not a big deal. Gravity varies by this much between different cities already. This is a good thing to keep in mind if you buy a digital scale. If your scale has a precision of more than two decimal places, you need to calibrate it with a test weight—the force of gravity at the scale factory isn't necessarily the same as the force of gravity at your house.
While you might not notice the increased gravity just yet, you'd notice the expansion. After a month, you'd see a lot of cracks opening up in long concrete structures and the failure of elevated roads and old bridges. Most buildings would probably be ok, although those anchored firmly into bedrock might start to behave unpredictably.[Just what you want in a skyscraper.]
At this point, astronauts on the ISS would start getting worried. Not only would the ground (and atmosphere) be rising toward them, but the increased gravity would also cause their orbit to slowly shrink. They'd need to evacuate quickly; they'd have at most a few months before the station reentered the atmosphere and deorbited.
t = 1 year:
After a year, gravity would be 5% stronger. You'd probably notice the weight gain, and you'd definitely notice the failure of roads, bridges, power lines, satellites, and undersea cables. Your pendulum clock would now be ahead by five days.
What about the atmosphere?
If the atmosphere isn't growing like the land and water are, air pressure would start dropping. This is due to a combination of factors. As gravity increases, then air gets heavier. But since that air is spread out over a larger area, the overall effect would be decreasing air pressure.
On the other hand, if the atmosphere is also expanding, surface air pressure would rise. After years had passed, the top of Mt. Everest would no longer be in the "death zone".[See What-If #64.] On the other hand, since you'd be heavier—and the mountain would be taller—climbing would be more work.
t = 5 years:
After five years, gravity would be 25% stronger. If you weighed 70 kg when the expansion started, you'd weigh 88 kg now.
Most of our infrastructure would have collapsed. The cause of the collapse would be the expanding ground below them, not the increased gravity. Surprisingly, most skyscrapers would hold up fine under much higher gravity.[Although I wouldn't trust the elevators.] For most of them, the limiting factor isn't weight, but wind.
t = 10 years:
After 10 years, gravity would be 50% stronger. In the scenario where the atmosphere isn't expanding, the air would become thin enough to be difficult to breathe even at sea level. In the other scenario, we'd be ok for a little while longer.
t = 40 years:
After 40 years, Earth's surface gravity would have tripled.[Over decades, the force of gravity would grow slightly faster than you'd expect, since the material in the Earth would compress under its own weight. The pressure inside planets is roughly proportional to the square of their surface area, so the Earth's core would be squeezed tightly.] At this point, even the strongest humans would only be able to walk with great difficulty. Breathing would be difficult. Trees would collapse. Crops wouldn't stand up under their own weight. Virtually every mountainside would see massive landslides as material sought out a shallower angle of repose.
Geologic activity would also accelerate. Most of the Earth's heat is provided by radioactive decay of minerals in the crust and mantle,[Although some radioactive elements, like uranium, are heavy, they get squeezed out of the lower layers because their atoms don't mesh well with the rock lattices at those depths. For more, see this chapter and this article.] and more Earth means more heat. Since the volume expands faster than the surface area, the overall heat flowing out per square meter will increase.
It's not actually enough to substantially warm the planet—Earth's surface temperature is dominated by the atmosphere and the Sun—but it would lead to more volcanoes, more earthquakes, and faster tectonic movement. This would be similar to the situation on Earth billions of years ago, when we had more radioactive material and thus a hotter mantle.
More active plate tectonics might be good for life. Plate tectonics play a key role in stabilizing the Earth's climate, and planets smaller than Earth (like Mars) don't have enough internal heat to sustain long-term geologic activity. A larger planet would allow for more geologic activity, which is why some scientists think that exoplanets slightly larger than Earth ("super-Earths") could be more friendly to life than Earth-sized ones.[Sasselov, Dimitar D.. The life of super-Earths: how the hunt for alien worlds and artificial cells will revolutionize life on our planet. New York: Basic Books, 2012.]
t = 100 years:
After 100 years, we'd be experiencing over six gees of gravity. Not only would we be unable to move around to find food, but our hearts would be unable to pump blood to our brains. Only small insects (and sea animals) would be physically able to move around. Perhaps humans could survive in specially-built controlled-pressure domes, moving around by keeping most of our bodies submerged in water.
Early scientists believed, based on the fossil record, that humans must be aquatic; it would be the only way they could have supported their weight against gravity.
Breathing in this situation would be difficult. It's hard to suck in air against the weight of the water, which is why snorkels can only work when your lungs are near the surface.
Outside of low-pressure domes, the air would become unbreathable for a different reason. At somewhere around 6 atmospheres, even ordinary air becomes toxic.[R.M. Franz and P.C. Schutte, Barometric hazards within the context of deep-level mining, The Journal of The South African Institute of Mining and Metallurgy] Even if we'd managed to survive all the other problems, by 100 years, we'd be dead from oxygen toxicity. Toxicity aside, breathing dense air is difficult simply because it's heavy.
Black hole?
When would the Earth eventually become a black hole?
It's hard to answer that, because the premise of the question is that the radius is steadily expanding while the density stays the same—whereas a black hole, the density increases.
The dynamics of really huge rocky planets aren't often analyzed, since there's no obvious way that they could form; anything that large will have enough gravity to gather hydrogen and helium during planet formation and become a gas giant.
At some point, our growing Earth would reach the point where adding more mass causes it to contract, rather than expand. After this point, it would collapse into something like a sputtering white dwarf or neutron star, and then—if its mass kept increasing—eventually become a black hole.
But before it gets that far ...
t = 300 years:
It's a shame humans wouldn't live this long, because at this point, something really neat would happen.
As the Earth grows, the Moon would, like all our satellites, gradually spiral inward.[Plummer, H. C., Note on the motion about an attracting centre of slowly increasing mass, Monthly Notices of the Royal Astronomical Society, Vol. 66, p.83] After several centuries, it would be close enough to the swollen Earth that the tidal forces between Earth and the Moon would be stronger than the gravitational forces holding the Moon together.
When the Moon passed this boundary—called the Roche limit—it would gradually break apart ...

If you liked it then you should have moved a mass inside its Roche limit.
... and Earth would, for a short time, have rings.
you became my giant lizard
If an asteroid was very small but supermassive, could you really live on it like the Little Prince?
Samantha Harper
Last week, we looked at at life on a giant world. This week, let's look at a small one.
'Did you eat my rose?' 'Maybe.'
The Little Prince, by Antoine de Saint-Exupéry, is a story about a traveler from a distant asteroid. It's simple and sad and poignant and memorable.[For another take on the Petit Prince, scroll down to the last section of this wonderful piece by Mallory Ortberg.] It's ostensibly a children's book, but it's hard to pin down who the intended audience is. In any case, it certainly has found an audience; it's among the best-selling books in history.

Personally, I always thought it looked like a snake that had swallowed a hat.
It was written in 1942. That's an interesting time to write about asteroids, because in 1942 we didn't actually know what asteroids looked like. Even in our best telescopes, the largest asteroids were only visible as points of light. In fact, that's where their name comes from—the word asteroid means "star-like."
We got our first confirmation of what asteroids looked like in 1971, when Mariner 9 visited Mars and snapped pictures of Phobos and Deimos.[Here's a picture of Phobos looking like the archetypical asteroid. The archived images from the mission are at the NASA Space Science Data Center, but strangely, the NSSDC refers readers to someone's personal Tripod page to browse the actual images.] These moons, believed to be captured asteroids,[Ironically, while Phobos and Deimos look like asteroids, new research suggests they're not. See Craddock, Robert A.. "Are Phobos And Deimos The Result Of A Giant Impact?". Icarus (2010)] solidified the modern image of asteroids as cratered potatoes.

A potato.
Before the 1970s, it was common for science fiction to assume small asteroids would be round, like planets.[Not always; plenty of people had a good idea of what they would look like. And there were stranger ideas ...]
The Little Prince took this a step further, imagining an asteroid as a tiny planet with gravity, air, and a rose. There's no point in trying to critique the science here, because (1) it's not a story about asteroids, and (2) it opens with a parable about how foolish adults are for looking at everything too literally.
So rather than trying to take things away from the story, let's see what strange new pieces science can add. If there really were a superdense asteroid with enough surface gravity to walk around on, it would have some pretty surprising properties.
If the asteroid has a radius of 1.75 meters, then in order to have Earth-like gravity at the surface, it would need to have a mass of about 500 million tons. This is roughly equal to the combined mass of every human on Earth.
If you stood on the surface, you'd experience tidal forces. Your feet would feel heavier than your head, which you'd feel as a gentle stretching sensation. It would feel like you were stretched out on a curved rubber ball, or were lying on a merry-go-round with your head near the center.
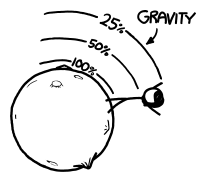
My back hasn't felt this good in years.
The escape velocity at the surface would be about 5 meters per second. That's slower than a sprint, but still pretty fast. As a rule of thumb, if you can't dunk a basketball, you wouldn't be able to escape by jumping straight up.

I believe I can flyyyy
However, the weird thing about escape velocity is that it doesn't matter which direction you're going.[... which is why it should really be called "escape speed"—the fact that it has no direction (which is the distinction between "speed" and "velocity") is actually very significant here.] If you go faster than the escape speed, as long as you don't actually go toward the planet, you'll escape. That means you might be able to leave our asteroid by running horizontally and jumping off the end of a ramp.

Wheeeeeeeeeeeeeee
If you didn't go fast enough to escape the planet, you'd go into orbit around it. Your orbital speed would be roughly 3 meters per second, which is a typical jogging speed.
Those ants down below look like people.
But this would be a weird orbit.
Tidal forces would act on you in several ways. If you reach your arm down toward the planet, it would be pulled much harder than the rest of you. And if you reach down with one arm, the rest of you gets pushed upward, which means other parts of your body feel even less gravity. Effectively, every part of your body would be trying to go in a different orbit.
A large orbiting object under these kinds of tidal forces—say, a moon—will generally break apart into rings. This wouldn't happen to you. However, your orbit would become chaotic and unstable.
These types of orbits were investigated in an interesting paper by Radu D. Rugescu and Daniele Mortari.[Rugescu, Radu D., Mortari, Daniele, "Ultra Long Orbital Tethers Behave Highly Non-Keplerian and Unstable", WSEAS Transactions on Mathematics, Vol. 7, No. 3, March 2008, pp. 87-94.] Their simulations showed that large, elongated objects follow strange patterns around their central bodies. Even their centers of mass don't move in the traditional ellipses; some adopt pentagonal orbits, while others spin chaotically and crash into the planet.
This is KSP on nightmare mode.
This type of analysis could actually have practical applications. There have been various proposals over the years to use long, whirling tethers to move cargo in and out of gravity wells—a sort of free-floating space elevator. Such tethers could transport cargo to and from the surface of the Moon, or to pick up spacecraft from the edge of the Earth's atmosphere. The inherent instability of many tether orbits poses an interesting challenge for this kind of project.
As for the residents of our superdense asteroid, they'd have to be careful; if they ran too fast, they'd be in serious danger of going into a tumble and losing their lunch.
Fortunately, vertical jumps would be fine.

Cleveland-area fans of French children's literature were disappointed by his decision to sign with the Miami Heat.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
When, if ever, will Facebook contain more profiles of dead people than of living ones?
Emily Dunham
Either the 2060s or the 2130s.

'Put on your headphones!' 'Can't. Ears fell off.'
There are not a lot of dead people on Facebook. The main reasons for this is that Facebook—and its users—are young. The average Facebook user has gotten older over the last few years, but the site is still used at a much higher rate by the young than by the old.[There are a zillion surveys confirming this, such as this one from eMarketer.]
The Past:
Based on the site's growth rate, and the age breakdown of their users over time,[You can get user counts for each age group from Facebook's create-an-ad tool, although you may want to try to account for the fact that Facebook's age limits cause some people to lie about their ages.] there are probably 10 to 20 million people who created Facebook profiles who have since died.
These people are, at the moment, spread out pretty evenly across the age spectrum. Young people have a much lower death rate than people in their sixties or seventies, but they make up a substantial share of the dead on Facebook simply because there have been so many of them using it.
The Future:
About 290,000 US Facebook users will die (or have died) in 2013. The worldwide total for 2013 is likely several million.[Note: In some of these projections, I used US age/usage data extrapolated to the Facebook userbase as a whole, because it's easier to find US census and actuarial numbers than to assemble the country-by-country for the whole Facebook-using world. The US isn't a perfect model of the world, but the basic dynamics—young people's Facebook adoption determines the site's success or failure while population growth continues for a while and then levels off—will probably hold approximately true. If we assume a rapid Facebook saturation in the developing world, which currently has a faster-growing and younger population, it shifts many of the landmarks by a handful of years, but doesn't change the overall picture as much as you might expect.] In just seven years, this death rate will double, and in seven more years it will double again.
Even if Facebook closes registration tomorrow, the number of deaths per year will continue to grow for many decades, as the generation who was in college between 2000 and 2020 grows old.

An elderly Cory Doctorow cosplaying by wearing what the future thinks he wore in the past.
The deciding factor in when the dead will outnumber the living is whether Facebook adds new living users—ideally, young ones—fast enough to outrun this tide of death for a while.
Facebook 2100:
This brings us to the question of Facebook's future.
We don't have enough experience with social networks to say with any kind of certainty how long Facebook will last. Most websites have flared up and then gradually declined in popularity, so it's reasonable to assume Facebook will follow that pattern.[I'm assuming, in these cases, that no data is ever deleted. So far, that's been a reasonable assumption; if you've made a Facebook profile, that data probably still exists, and most people who stop using a service don't bother to delete their profile. If that behavior changes, or if Facebook performs a mass purging of their archives, the balance could change rapidly and unpredictably.]
In that scenario, where Facebook starts losing market share later this decade and never recovers, Facebook's crossover date—the date when the dead outnumber the living—will come sometime around 2065.

But maybe it won't. Maybe it will take on a role like the TCP protocol, where it becomes a piece of infrastructure on which other things are built, and has the inertia of consensus.
If Facebook is with us for generations, then the crossover date could be as late as the mid-2100s.

That seems unlikely. Nothing lasts forever, and rapid change has been the norm for anything built on computer technology. The ground is littered with the bones of websites and technologies that seemed like permanent institutions ten years ago.
It's possible the reality could be somewhere in between.[Of course, if there's a sudden rapid increase in the death rate of Facebook users—possibly one that includes humans in general—the crossover could happen tomorrow.] We'll just have to wait and find out.
The fate of our accounts:
Facebook can afford to keep all our pages and data indefinitely. Living users will always generate more data than dead ones, and the accounts for active users are the ones that will need to be easily accessible. Even if accounts for dead (or inactive) people make up a majority of their users, it will probably never add up to a large part of their overall infrastructure budget.
More important will be our decisions. What do we want for those pages? Unless we demand that Facebook deletes them, they will presumably, by default, keep copies of everything forever. Even if they don't, other data-vacuuming organizations will.
Right now, next-of-kin can convert a dead person's Facebook profile into a memorial page. But there are a lot of questions surrounding passwords and access to private data that we haven't yet developed social norms for. Should accounts remain accessible? What should be made private? Should next-of-kin have the right to access email? Should memorial pages have comments? How do we handle trolling and vandalism? Should people be allowed to interact with dead user accounts? What lists of friends should they show up on?
These are issues that we're currently in the process of sorting out by trial and error. Death has always been a big, difficult, and emotionally charged subject, and every society finds different ways to handle it.
The basic pieces that make up a human life don't change. We've always eaten, learned, grown, fallen in love, fought, and died. In every place, culture, and technological landscape, we develop a different set of behaviors around these same activites.
Like every group that came before us, we're learning how to play those same games on our particular playing field. We're developing, through sometimes messy trial and error, a new set of social norms for dating, arguing, learning, and growing on the internet. Sooner or later, we'll figure out how to mourn.

★★☆☆☆
Happy Halloween!
with the van, we went around in the cold, always dreaming of a better place and hugging hot at night
How big of a lawn would you have to have so that when you finished mowing you'd need to start over because the grass has grown?
Nick Nelson
According to the Turfgrass Extension and Outreach program at UIUC,[The Morrow cornfields operated by the university are the most valuable cornfields in the world, and part of one of the world's longest-running scientific experiments.] every mowing should remove one third of the grass blade's height.

The UIUC Turfgrass 2013 Battle Plan, I hope.
Grass grows slower or faster depending on the weather, but we'll assume an average growth rate of 0.2 inches per day. This figure comes from Mowing Your Lawn, a document published by by Iowa State's Yard and Garden Extension program (which, I like to imagine, has a vicious and occasionally bloody rivalry with the UIUC Turfgrass crew).
A typical pushmower at a fast walking speed can mow a little under a square meter per second. If you mowed without stopping from 8:00 AM to 6:00 PM, you would cover about 25,000 square meters.[or 6 acres, or 2.5 hectares, or 7,500 square fathoms, or 8,500 square smoots, or 5,300 Shrouds of Turin] To maintain your lawn at a height of four inches, you would need to mow it every ten days. If you mowed more or less frequently, you could risk damaging the lawn—or, worse, incur the wrath of UIUC.
At ten hours of mowing per day, you could cover a quarter of a square kilometer before you'd have to circle back to the beginning and start over. If the entire area of Vatican City, indoors and out, were covered in perennial ryegrass,[Perhaps due to an ill-advised UIUC undergraduate project] you would be able to keep about half of it neatly trimmed.

With the help of Pope Emeritus Benedict, they could cover the whole thing!
You could improve on this with a larger, faster mower. An oversized rider mower at 12 miles per hour[The maximum listed in the Cub Cadet rider mower acres-per-hour chart ] could mow as much as two square kilometers, which Wolfram|Alpha helpfully tells me is 0.5% to 1% of an adult male cougar's home range.
A cougar chasing down a deere.
In 2010, Bobby Cleveland set a world record for the top speed in a riding lawnmower, hitting 96 mph. This record was set as part of a rivalry with the British lawnmower driver Don Wales.[Really.]
In a blow to its national pride, the US has lost that record. Sometime in the last few years, the magazine Top Gear commissioned Honda to build them an even faster lawnmower. A few months ago, this mower—which shoots flames from the exhaust pipe—broke 100 mph on a test track in France.["First tests of '130mph' lawnmower", BBC News Technology, 17 July 2013] The builders claim it will eventually reach 130 mph. The mower is still capable of cutting grass (using a custom wire mechanism), but when running at top speed the trimmer is removed for safety reasons.
With the Top Gear mower, what's the maximum area we could cut?
Let's set safety aside and assume we can leave the mower's cutting mechanism in place. Let's also assume that the mower can cut a strip two meters wide while running at top speed.
Under those assumptions, if the mower is run for 24 hours a day, seven days a week ...
Since cougars aren't found in Europe, perhaps 'top speed by a rider mower carrying a cougar' is a record that Americans can more reliably dominate.
... it could just about keep one adult male cougar's home range neatly trimmed.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
I was absentmindedly stirring a cup of hot tea, when I got to thinking, "aren't I actually adding kinetic energy into this cup?" I know that stirring does help to cool down the tea, but what if I were to stir it faster? Would I be able to boil a cup of water by stirring?
Will Evans
No.
The basic idea makes sense. Temperature is just kinetic energy. When you stir tea, you're adding kinetic energy to it, and that energy goes somewhere. Since the tea doesn't do anything dramatic like rise into the air or emit light, the energy must be turning to heat.

Am I making tea wrong?
The reason you don't notice the heat is that you're not adding very much of it. It takes a huge amount of energy to heat water; by volume, it has a greater heat capacity than any other common substance.[Hydrogen and helium have a higher heat capacity by mass, but they're diffuse gasses. The only other common substance with a higher heat capacity by mass is ammonia. All three of these lose to water when measured by volume.]
If you want to heat water from room temperature to nearly boiling in two minutes, you'll need a lot of power:
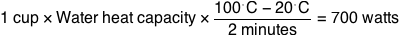
(Note: Pushing almost-boiling water to boiling takes a large burst of extra energy on top of what's required to heat it to the boiling point—this is called the enthalpy of vaporization.)
Our formula tells us that if we want to make a cup of hot water in two minutes, we'll need a 700-watt power source. A typical microwave uses 700 to 1100 watts, and it takes about two minutes to heat a mug of water to make tea. It's nice when things work out![If they didn't, we'd just blame "inefficiency" or "vortices".]
700 watts for two minutes is an awful lot of energy. When water falls from the top of Niagara Falls, it gains kinetic energy, which is converted to heat at the bottom. But even after falling that great distance, the water only heats up by a fraction of a degree.[ ] To boil a cup of water, you'd have to drop it from higher than the top of the atmosphere.
] To boil a cup of water, you'd have to drop it from higher than the top of the atmosphere.

(The British Felix Baumgartner)
How does stirring compare to microwaving?
Based on figures from industrial mixer engineering reports,[Brawn Mixer, Inc., Principles of Fluid Mixing (2003)] I estimate that vigorously stirring a cup of tea adds heat at a rate of about a ten-millionth of a watt. That's completely negligible.[Tea loses heat a much higher rate than this. See: Ben Harden, Tea temperature vs. Time graph]
The physical effect of stirring is actually a little complicated.[In some situations, mixing liquids can actually help keep them warm. Hot water rises, and when a body of water is large and still enough (like the ocean) a warm layer forms on the surface. This warm layer radiates heat much more quickly than a cold layer would. If you disrupt this hot layer by mixing the water, the rate of heat loss decreases.
This is why hurricanes tend to lose strength if they stop moving forward—their waves churn up cold water from the depths, cutting them off from the thin layer of hot surface water that was their main source of energy.] Most of the heat is carried away from teacups by the air convecting over them, and so they cool from the top down. Stirring brings fresh hot water from the depths, so it can help this process. But there are other things going on—stirring disturbs the air, and it heats the walls of the mug. It's hard to be sure what's really going on without data.
Fortunately, we have the internet. StackExchange user drhodes measured the rate of teacup cooling from stirring vs. not stirring vs. repeatedly dipping a spoon into the cup vs. lifting it. Helpfully, drhodes posted both high-resolution graphs and the raw data itself, which is more than you can say for a lot of journal articles.
The conclusion: It doesn't really matter whether you stir, dip, or do nothing; the tea cools at about the same rate (although dipping the spoon in and out of the tea cooled it slightly faster).
Which brings us back to the original question: Could you boil tea if you just stirred it hard enough?
No.
The first problem is power. 700 watts is about a horsepower, so if you want to boil tea in two minutes, you'll need at least one horse to stir it hard enough.

But I can't understand the microwave buttons because they're confusing and I'm a horse.
You can reduce the power requirement by heating the tea over a longer period of time, but if you reduce it too far the tea will be cooling as fast as you're heating it.
Even if you could churn the spoon hard enough—tens of thousands of stirs per second—fluid dynamics would get in the way. At those high speeds, the tea would cavitate; a vacuum would form along the path of the spoon and stirring would become ineffective.
And if you stir hard enough that your tea cavitates, its surface area will increase very rapidly, and it will cool to room temperature in seconds:

At least the teacup wasn't half empty.
No matter how hard you stir your tea, it's not going to get any warmer.
everything we want is possible, that's how well we work
What is the furthest one human being has ever been from every other living person? Were they lonely?
Bryan J. McCarter
It's hard to know for sure!
The most likely suspects are the six Apollo command module pilots who stayed in lunar orbit during a Moon landing: Mike Collins, Dick Gordon, Stu Roosa, Al Worden, Ken Mattingly, and Ron Evans.
Each of these astronauts stayed alone in the command module while two other astronauts landed on the Moon. At the highest point in their orbit, they were about 3,585 kilometers from their fellow astronauts.
From another point of view, this was the farthest the rest of humanity has ever managed to get from those jerk astronauts.
You'd think astronauts would have a lock on this category, but it's not so cut-and-dry. There are a few other candidates who come pretty close!
It's hard to get 3,585 kilometers[Because of the curve of the Earth, you actually have to go 3,619 kilometers across the surface to qualify.] from a permanently inhabited place. The Polynesians, who were the first humans to spread across the Pacific, might have managed it, but this would have required a lone sailor to travel awfully far ahead of everyone else. It may have happened—perhaps by accident, when someone was carried far from their group by a storm—but we're unlikely to ever know for sure.
Once the Pacific was colonized, it got a lot harder to find regions of the Earth's surface where someone could achieve 3,585 kilometer isolation. Now that the Antarctic continent has a permanent population of researchers, it's almost certainly impossible.
During the period of Antarctic exploration, a few people have come close to beating the astronauts, and it's possible one of them actually holds the record. One person who came very close was Robert Scott.
Robert Falcon Scott was a British explorer who met a tragic end. Scott's expedition reached the South Pole in 1911, only to discover that Norwegian explorer Roald Amundsen had beaten him there by several months. The dejected Scott and his companions began their trek back to the coast, but they all died while crossing the Ross Ice Shelf.
The last surviving expedition member would have been, briefly, one of the most isolated people on Earth.[Amundsen's expedition had left the continent by then.] However, he (whoever he was) was still within 3,585 kilometers of a number of humans, including some other Antarctic explorer outposts as well as the Māori on Rakiura (Stewart Island) in New Zealand.
There are plenty of other candidates. Pierre François Péron, a French sailor, says he was marooned on Île Amsterdam in the southern Indian Ocean. If so, he came close to beating the astronauts, but he wasn't quite far enough from Mauritius, southwestern Australia, or the edge of Madagascar to qualify.
We'll probably never know for sure. It's possible that some shipwrecked 18th-century sailor drifting in a lifeboat in the Southern Ocean holds the title of most isolated human. However, until some clear piece of historic evidence pops up, I think the six Apollo astronauts have a pretty good claim.
Which brings us to the second part of Bryan's question: Were they lonely?
After returning to Earth, Apollo 11 command module pilot Mike Collins said he did not feel at all lonely. He wrote about the experience in his book Carrying the Fire: An Astronaut's Journeys:
Far from feeling lonely or abandoned, I feel very much a part of what is taking place on the lunar surface ... I don't mean to deny a feeling of solitude. It is there, reinforced by the fact that radio contact with the Earth abruptly cuts off at the instant I disappear behind the moon.
I am alone now, truly alone, and absolutely isolated from any known life. I am it. If a count were taken, the score would be three billion plus two over on the other side of the moon, and one plus God knows what on this side.
Al Worden, the Apollo 15 command module pilot, even enjoyed the experience:[BBC Future interview with Al Wolden (April 2, 2013)]
There's a thing about being alone and there's a thing about being lonely, and they're two different things. I was alone but I was not lonely. My background was as a fighter pilot in the air force, then as a test pilot–and that was mostly in fighter airplanes–so I was very used to being by myself. I thoroughly enjoyed it. I didn't have to talk to Dave and Jim any more ... On the backside of the Moon, I didn't even have to talk to Houston and that was the best part of the flight.
Introverts understand; the loneliest human in history was just happy to have a few minutes of peace and quiet.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
How close would you have to be to a supernova to get a lethal dose of neutrino radiation?
(Overheard in a physics department)
The phrase "lethal dose of neutrino radiation" is a weird one. I had to turn it over in my head a few times after I heard it.
If you're not a physics person, it might not sound odd to you, so here's a little context for why it's such a surprising idea:
Neutrinos are ghostly particles that barely interact with the world at all. Look at your hand—there are about a trillion neutrinos from the Sun passing through it every second.

Ok, you can stop looking at your hand now.
The reason you don't notice the neutrino flood is that neutrinos hardly interact with ordinary matter at all. On average, out of that massive flood, only one neutrino will "hit" an atom in your body every few years.[Less often if you're a child, since you have fewer atoms to be hit. Statistically, my first neutrino interaction probably happened somewhere around age 10.]
In fact, neutrinos are so shadowy that the entire Earth is transparent to them; nearly all of the Sun's neutrino flood goes straight through it unaffected. To detect neutrinos, people build giant tanks filled with hundreds of tons of material in the hopes that they'll register the impact of a single solar neutrino.
This means that when a particle accelerator (which produces neutrinos) wants to send a neutrino beam to a detector somewhere else in the world, all it has to do is point the beam at the detector—even if it's on the other side of the Earth!
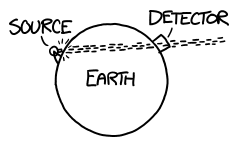
Hey, these ones arrived faster than light! Wait, no.
That's why the phrase "lethal dose of neutrino radiation" sounds weird—it mixes scales in an incongruous way. It's like the idiom "knock me over with a feather" or the phrase "football stadium filled to the brim with ants".[Which would still be less than 1% of the ants in the world.] If you have a math background, it's sort of like seeing the expression "ln(x)e"—it's not that, taken literally, it doesn't make sense, but it's hard to imagine a situation where it would apply.[If you want to be mean to first-year calculus students, you can ask them to take the derivative of ln(x)e dx. It looks like it should be "1" or something, but it's not.]
Similarly, it's so hard to get enough neutrinos to compel even a single one of them to interact with matter, making it hard to picture a scenario in which there'd be enough of them to affect you.
Supernovae["Supernovas" is also fine. "Supernovii" is discouraged.] provide that scenario. The physicist who mentioned this problem to me told me his rule of thumb for estimating supernova-related numbers: However big you think supernovae are, they're bigger than that.
Here's a question to give you a sense of scale:
Which of the following would be brighter, in terms of the amount of energy delivered to your retina:
A supernova, seen from as far away as the Sun is from the Earth, or
The detonation of a hydrogen bomb pressed against your eyeball?

Can you hurry up and set it off? This is heavy.
Applying the physicist rule of thumb suggests that the supernova is brighter. And indeed, it is ... by nine orders of magnitude.
That's why this is a neat question; supernovae are unimaginably huge and neutrinos are unimaginably insubstantial. At what point do these two unimaginable things cancel out to produce an effect on a human scale?
A paper by radiation expert Andrew Karam provides an answer.[Karam, P. Andrew. "Gamma And Neutrino Radiation Dose From Gamma Ray Bursts And Nearby Supernovae." Health Physics 82, no. 4 (2002): 491-499.] It explains that during certain supernovae, the collapse of a stellar core into a neutron star, 1057 neutrinos can be released (one for every proton in the star that collapses to become a neutron).
Karam calculates that the neutrino radiation dose at a distance of one parsec[3.262 light-years, or a little less than the distance from here to Alpha Centauri.] would be around half a nanosievert, or 1/500th the dose from eating a banana.[xkcd.com/radiation]
A fatal radiation dose is about 4 sieverts. Using the inverse-square law, we can calculate the radiation dose:
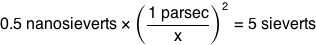
 2.3 AU is a little more than the distance between the Sun and Mars.
2.3 AU is a little more than the distance between the Sun and Mars.
Core collapse supernovae happen to giant stars, so if you observed a supernova from that distance, you'd probably be inside the outer layers of the star that created it.
GRB 080319B was the most violent event ever observed—especially for the people who were floating right next to it with surfboards.
The idea of neutrino radiation damage reinforces just how big supernovae are. If you observed a supernova from 1 AU away—and you somehow avoided being being incinerated, vaporized, and converted to some type of exotic plasma—even the flood of ghostly neutrinos would be dense enough to kill you.
If it's going fast enough, a feather can absolutely knock you over.
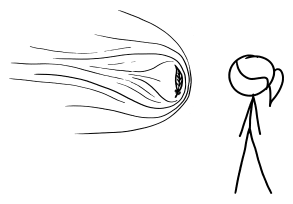
Dude, AGAIN? Can you just pitch like a normal person?
i like you
How much of the Earth's currently-existing water has ever been turned into a soft drink at some point in its history?
Brian Roelofs
0.0000005%.
First, a tiny bit of background: In the beverage industry, "soft drink" technically refers to any non-alcoholic packaged beverage, but it's commonly used to mean carbonated beverages.[In the US, the word people use to refer to a generic carbonated beverage—"soda" vs. "pop" vs. "coke"—strongly depends on where they live.] Carbonated water was first produced in the 1700s, and gained popularity as "tonic water" (carbonated water mixed with quinine powder, which has anti-malaria properties), and in carbonated lemonade.[Shahan Cheong, Taking the Waters: The History of the Modern Soft-Drink, Not Yet Published (blog post)]
The vast majority of all soft drinks ever consumed have been consumed in the last 40 years. Carbonated beverages were fairly popular in the industrialized world throughout the 20th century, but population growth and the spread of companies like Coca-Cola into the developing world mean that the total soda consumption per year has grown relatively fast.
Total soft drink consumption in 2013 was about 188 billion liters. That's 26 liters per person annually, or 70 mL/day.[MarketLine, Carbonated Soft Drinks: Global Industry Guide] (In the US, the average was 170 liters, or about one 16-oz drink per person per day[Dan Check, Matt Dodson, and Chris Kirk, Americans Drink More Soda Than Anyone Else (slate.com)]).

And each soda is a couple of Cadbury eggs.
Over the past several centuries, humans have probably consumed about 6.5 trillion liters of carbonated beverages.[This is a ballpark guess based on population growth and some rough estimates of when soda-drinking became popular in different parts of the world.]
That's a lot, certainly. For example, it's enough to fill every house and apartment in the US to a depth of 12 inches:
BRB, searching Amazon for 'floor-length straw'.
Even if we assume that every soda is made from an entirely new batch of water, and doesn't include any water from previous sodas, it still represents a tiny fraction of the world's fresh water, and an even tinier fraction of the total volume of the oceans.
What if we expand the question to cover all drinking water? What percentage of water molecules have been drunk[Drank? Drinked? Drankéd?] by someone at some point?
Humans have been around for a few hundred thousand years, and the total number of humans who have ever lived is usually estimated to be around 110 billion. The question of how much water we should drink per day is the subject of furious debate—the "8 glasses" thing seems to be a myth—but the amount of water we actually drink per day seems to be about a liter.[EPA, Estimated Per Capita Water Ingestion and Body Weight in the United States–An Update (2004)] This amount varies a little depending on climate, but if we assume the average historical human drank a liter of water per day for 40 years,[This is a rough ballpark estimate; it's lower than the 70 or 80 years you might expect because we have to account for the changing human lifespans throughout history and the decreased water consumption by children.] then our species has drunk about 100 trillion liters of water in total.
100 trillion liters (100 km3) is still very little compared to even the volume of all rivers (1,200 km3). This means that, since our drinking water passes through the water cycle and is quickly diluted by rivers and oceans, the majority of the water molecules we drink have never been drunk by any other human.[On the other hand, it's just about guaranteed that some of the water molecules in any mouthful have been drunk by someone else.]
But we're just one species.
Dinosaurs, as a taxonomic group, have been around[They're still around!] for 230 million years, but their heyday was the mid-to-late Jurassic period. In this period, there were probably around 5 trillion kilograms of dinosaur alive at any given time.[Jerzy Trammer, "Differences in global biomass and energy use between dinosaurs and mammals", Acta Geologica Polonica, Vol. 61 (2011), No. 2, pp. 125–132] (Today, there are probably only a few hundred billion kilograms of living dinosaur,[I haven't been able to find an estimate for total global bird biomass, but I'll take any chance to cite my favorite journal article ever: "How Many Birds Are There?", by Kevin J. Gaston and Tim M. Blackburn, which estimates the total number at about 300 billion. A later paper lowered the estimate to about 80 billion, so unless the average bird weighs 140 lbs, there is far less dinosaur in the world today than in the Jurassic.] 50 billion of it chicken).
If we assume Jurassic dinosaur water requirements were similar to mammal ones,[Animal weights and their food and water requirements] then this suggests dinosaurs drank something like 1022 or 1023 liters of water during the Mesozoic era—more than the total volume of the oceans (1021 liters).
The average "residence time" of water in the oceans—the amount of time a water molecule spends there before moving into another part of the water cycle—is about 3,000 years,[K. L. Schulz, Water in the Biosphere] and no part of the water cycle traps water for more than a few hundred thousand years. This means we can assume that, over timescales of millions of years, Earth's water is thoroughly mixed—and dinosaurs had plenty of time to drink it all many times over.
This means that while the chances are that most of the water in your soda has never been in another soda, almost all of it has been drunk by at least one dinosaur.

::sluuuuuurp:: RRRRRR 'Sorry.'
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
I use one of those old phones where you type with numbers—for example, to type "Y", you press 9 three times. Some words have consecutive letters on the same number. When they do, you have to pause between letters, making those words annoying to type. What English word has the most consecutive letters on the same key?
Stewart Bishop
We can answer that question with the following headache-inducing shell command, which finds all words in a given list which use the same key a bunch of times in a row:
cat wordlist.txt | perl -pe 's/^(.*)\$/\L\$& \U\$&/g' | tr 'ABCDEFGHIJKLMNOPQRSTUVWXYZ' '2223334445556667777888999' | grep -P "(.)\1\1\1\1\1"
The winner, according to this script, is nonmonogamous, which requires you to type seven consecutive letters (nonmono) with the "6" key.[It's actually tied with nonmonotonic. These no doubt both lose to more obscure words which weren't in the wordlists I used.]
Phone Keyboard Sentences
It's rare for a word to have all its letters on the same key; the longest common ones are only a few letters.[Like "tutu".] Nevertheless, using only these words, we can write a high def MMO on TV, a phrase whose words use only one number key each.
Just one more hour.
There are plenty of other phrases like this, although some of them are a bit of a stretch:

Pony up!
Typing issues like this aren't limited to old phone keyboards. For any text input system, you can find phrases which are weird to type.
QWERTY Keyboards
It's a well-known piece of trivia among word geeks that "stewardesses" is the longest common word you can type on a QWERTY keyboard using only the left hand.
In fact, it's possible to write entire sentences with just the left hand. For example, try typing the words We reserved seats at a secret Starcraft fest. Weird, huh?
Let's take a look at a few more sentences—written with the help of some even messier shell commands and Python scripts[I constructed these sentences by searching text logs for sentence fragments that fit a particular constraint, then randomly connecting those groups together using a technique called Markov chaining. You can see the code I used here.]—which follow various constraints:
Left hand only

Totally worth it.

MEET SINGLE FERRETS IN YOUR AREA TONIGHT
Right hand only

How DARE you.

OMG puppy milk!
Home row only

He looked at the contents and immediately fell dead.

She's nice, though!

Crisp, though.
Top row only
Also, we brought some milk!

The worst part is it actually IS really good.
And lastly, if anyone wants to know why you're not more active on social media, you only need the top row to explain that you're ...

Or too pretty to retweet.
we turned to sleep deprived zombies in the streets of frankfurt and kissed for the new year, we had a year ahead just for the two of us, we had a life together
At what point in human history were there too many (English) books to be able to read them all in one lifetime?
Gregory Willmot
This is a complicated question. Getting accurate counts of the number of extant books at different times in history is very hard bordering on impossible. For example, when the Library of Alexandria burned, a lot of writing was lost,[On the other hand, a lot of Egyptian readers were probably excited to get out of overdue book fines.] but how much writing was lost is hard to pin down. Some estimates range from 40,000 books to 532,800 scrolls,[The Great Library of Alexandria] and other writers say that all those numbers are implausible.
Researchers Eltjo Buringh and Jan Luiten van Zanden used historical book catalogs to put together statistics on the number of books (or manuscripts) published annually per region.[Charting the “Rise of the West”: Manuscripts and Printed Books in Europe, A Long-Term Perspective from the Sixth through Eighteenth Centuries ] By their figures, the rate of publication in the British Isles probably passed one manuscript per day in around the year 1075 CE.
Most of the manuscripts published in 1075 weren't in English, or even the variants of English common at the time. In 1075, literature was typically written in some form of Latin or French, even in areas where Old English was commonly spoken on the street.
The Canterbury Tales (written in the late 1300s) were part of a move toward vernacular English as a literary language, although they're not exactly readable to a modern eye:
Wepyng and waylyng, care and oother sorwe
I knowe ynogh, on even and a-morwe,'
Quod the Marchant, 'and so doon oother mo
That wedded been.

If my 9th grade English teacher is reading, ignore this, I TOTALLY understand that verse.
Even if we know how many manuscripts were published per year, in order to answer Gregory's question, we still need to know how long it takes to read a manuscript.
Rather than trying to figure out how long all the lost books and codices are, we can step back and take a longer view of things.
Writing speed
Tolkien wrote Lord of the Rings in 11 years, which means that he wrote at an average pace of 125 words per day, or less than 0.085 word per minute. Harper Lee wrote the 100,000-word To Kill a Mockingbird in two and a half years, for an average of 100 words per day, or 0.075 words per minute. Since To Kill a Mockingbird is her only published book, her lifetime average is 0.002 words per minute, or about three words per day.
Some writers are substantially faster. In the preface to Opus 200, the prolific writer Isaac Asimov estimated that he had published about 15,000,000 words between age 30 and 50. His average over his writing career might have been around 1 word per minute, and at times he was averaging writing several thousand words per day. (Over his entire life, his average dips as low as 0.5 words per minute.) Some pulp writers have even higher averages.
It's reasonable to assume historical writers had a similar range of speeds. You might point out that typing on a keyboard is more than twice as fast as writing a manuscript in longhand. But typing speed isn't a writer's bottleneck. After all, at a typing speed of 70 words per minute, it should only take 24 hours to type out To Kill a Mockingbird.

Well, they say to write what you know.
Typing and writing speeds are so different because the limit on writing speed is how quickly our brains can organize, produce, and edit stories. This "storytelling speed" has probably changed much less over time than our physical writing speed has.
This gives us a much better way to estimate when the number of books became too large to read.
The average person can read at 200-300 words per minute. If the average living writer, over their entire lifetime, falls somewhere between Isaac Asimov and Harper Lee, they might produce 0.05 words per minute over their entire lifetime.
If you were to read for 16 hours a day at 300 words per minute,[For an average of 200 words per minute.] you could keep up with a world containing an average population of 100,000 living Harper Lees or 400 living Isaac Asimovs.
Isaacs Asimov?
If we estimate that during their active periods, writers are producing somewhere between 0.1 and 1 word per minute, then one dedicated reader might be able to keep up with a population of about 500 or 1,000 active writers. The answer to Gregory's question—the date at which there were too many English books to read in a lifetime—happened sometime before the population of active English writers reached a few hundred. At that point, catching up became impossible.
The magazine Seed estimates that the total number of authors reached this point around the year 1500 and has continued rising rapidly ever since.[Seed: A Writing Revolution] The number of active English writers crossed this threshold shortly thereafter, around the time of Shakespeare, and the total number of books in English probably passed the lifetime reading limit sometime in the late 1500s.
On the other hand, how many of them would you want to read? If you go to goodreads.com/book/random, you can see a semi-random sample of what you'd be reading. Here's what came up for me:
So far, I've read ... the Goosebumps book.
To make it through the rest, I might need to recruit some help.

'Can't I skip my OWN books? There are so many of them!' 'No, Isaac. You know the rules.'
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
What height would humans reach if we kept growing through our whole development period (i.e. till late teens/early twenties) at the same pace as we do during our first month?
Maria
Tall.
According to the National Center for Health Statistics, the average newborn's height (length) is approximately 0.5 meters,[or 0.56 meters in heels.] or a quarter of the diameter of the Death Star thermal exhaust port.

Babies are a little less than a quarter of a womp rat long.
From this initial height of 0.5 meters, they grow to about 1.5 or 2.0 meters:
The timing of male and female puberty roughly cancel out, so average height grows steadily throughout the Kidz Bop years.
Babies grow fastest right after they're born. During their first month, infants grow about 4.4 centimeters, ten times their growth rate during their early teenage years.
A chart showing a lower bound for the length of a baby-eating snake versus age of its victims.
In Maria's scenario, this growth rate continues until about age 20:
We're going to need a longer snake.
Let's follow that child's growth over the years.
By its first birthday, the baby would be a meter long:
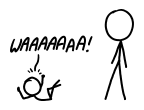
Go get another one-gallon bottle.
At 2 years and 3 months, the kid would reach 169 centimeters (5'7"), the average adult height in the US.
Blends right in!
By age 3, we'd have a 2.08 meter (6'10") toddler, taller than Darth Vader ...

I find the bug you found disturbing.
... and much taller than Yoda:

MMmmmm. An excellent bug this is!
By age 4, the child would be nearly nine feet tall, able to dunk a basketball without jumping.[A 7'8" Harlem Globetrotters player can almost dunk without jumping, so the threshold for a clear no-jump dunk is probably around 8 feet.]

But what I really want to do is play professional baseball.
A few months later, the kid would surpass Robert Wadlow to become the tallest human in history.
At age 5, the child would be $ \pi $ meters tall (10'4"):
I mean, 0.5 tau meters.
At age 7, the child would be 4.2 meters tall, able to stare down a T-rex:
*purrrrr*
By age 10, the child would be 5.8 meters tall (19 feet). If we assume these giants are proportioned like adult humans, this kid would weigh over a metric ton.

Still only about 0.2 tyrannosaurs.
Actual humans wouldn't be able to grow to such heights. Thanks to the square-cube law, our bones would be too thin to support our weight and our hearts would be unable to pump blood around our bodies. Even breathing would be difficult; we might be able to position ourselves to keep our airways opened, but to breathe in a lungful of air would require very high airflow rates; we'd experience tornado winds all the way down our airways.
Our giant would reach a final height of between 10 and 12 meters, assuming growth tapered off around age 20. At that height, they'd be able to comfortably dunk a basketball while keeping one hand on the court outside the three-point line.[A creative NBA 2K3 mod shows us what that player might look like.]

What do you mean 'against the rules'? Your team has a freakin' golden retriever!
In addition to the insurmountable health problems, someone with this rapid growth rate would face another hardship.
To ride roller coasters, you have to be above a certain minimum height. However, they generally also have a maximum height.
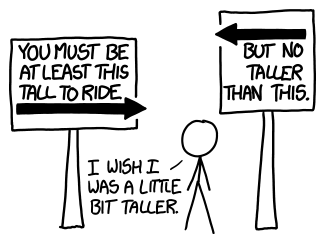
You must have a core temperature between 33°C and 41°C to ride.
Bizarro, a coaster at Six Flags New England, has a minimum height of 137 cm (4'6") and a maximum height of 193 cm (6'4"). Our child would be tall enough to ride Bizarro at age 2 ... and too tall by age 3. Their coaster-riding window would last only 387 days.
It's a sad truth: Roller coasters just aren't for everyone.
That night, the roller coaster's empty cars are all mysteriously lifted from their tracks and smashed to the ground.
and we flew, for each of us, it was the first time we were flying with someone and i couldn't have been happier to be with you
If a T-rex were released in New York City, how many humans/day would it need to consume to get its needed calorie intake?
Tony Schmitz
About half of an adult, or one ten-year old child:
Shoot, I forgot to eat one yesterday. Am I allowed to double up?
Tyrannosaurus rex weighed about as much as an elephant.[This always seemed a little off to me; my mental image of elephants is that they're in the same size range as cars or trucks, whereas T-rex, as Jurassic Park showed, is big enough to stomp on cars. But a Google image search for car+elephant shows elephants looming over cars just like the T-rex in Jurassic Park. So, great, now I'm also afraid of elephants.]
Utahraptor will be so jealous.
No one is totally sure what dinosaur metabolism looked like, but the best guesses for how much food T-rex ate seem to cluster around 40,000 calories per day.[Food calories (kcal). Sources: This and this, and this with some notes from this and distraction from this. ]
If we assume dinosaurs had metabolisms similar to today's mammals, they'd eat a lot more than 40,000 calories each day. But the current thinking is that while dinosaurs were more active (loosely speaking, "warm-blooded") than modern snakes and lizards, very large dinosaurs probably had metabolisms that more closely resembled komodo dragons than elephants and tigers.[For big sauropods, we know this must be the case, because otherwise they would overheat. However, there's a lot of uncertainty surrounding T-rex-sized dinosaurs.]
Next, we need to know how many calories are in a human. This number is helpfully provided, by Dinosaur Comics author Ryan North, on this wonderful t-shirt. Ryan's shirt tells us that an 80-kg human contains about 110,000 calories of energy.
Therefore, a T-rex would need to consume a human every two days or so.[Although a T-rex would likely be willing to eat several days to weeks worth of food in one meal, so if it has the option, it might eat a bunch of people at a time, then go for a while without eating.] The city of New York had 239,736 births in 2011, which could support a population of about 1,000 tyrannosaurs. However, this ignores immigration—and, more importantly, emigration, which would probably increase substantially in this scenario.

I wonder if a tyrannosaur could fit into an MTA subway car.
The 33,000 McDonald's restaurants worldwide sell something like 15 billion hamburger patties per year,[They stopped reporting the "x billions served" number on their signs, but this website has some extrapolations.] for an average of 1,245 burgers per restaurant per day. 1,245 burgers is about 600,000 calories, which means that each T-rex only needs about 80 hamburgers per day to survive, and one McDonald's could support over a dozen tyrannosaurs on hamburgers alone.

One of them sleeps in the ball pit. Tell your kids!
Ands if you live in New York, and you see a T-rex, don't worry. You don't have to choose a friend to sacrifice; just order 80 burgers instead.
And then if the T-rex goes for your friend anyway, hey, you have 80 burgers.

More of an acquaintance, really.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
What if we were to dump all the tea in the world into the Great Lakes? How strong, compared to a regular cup of tea, would the lake tea be?
Alex Burman
Weak, bordering on homeopathic.
The standard cup of tea, as described by the International Organization for Standardization in ISO 3103, contains two grams of tea per 100 mL of water.[Further ISO standards concerning tea include ISO 3720 (black tea), ISO 11287 (green tea), and ISO 14502-2 (the difference between black tea and green tea).] The Great Lakes have a volume of about 22,600 cubic kilometers, which means we would need about 450 billion tons of tea to reach proper strength.
According to the Tea Board of India, one year's global tea harvest totals only about 4.8 million tons,[Using figures from this report extrapolated forward to 2014.] only 1/100,000th of what we'd require to make Great Lake Tea. If we dumped those 4.8 million tons into the lakes, the resulting tea would be about as strong as if we'd dripped two drops of tea in a bathtub.[Technically, calling this kind of tea "homeopathic" is an exaggeration, since substances in homeopathy are diluted way more than this.] Proper bathtub tea, of course, requires one 3-kg bag.
Cue strong opinions about adding sugar to bathtubs.
For better lake tea, we should find a lake with a volume of 240 million cubic meters (0.24 cubic kilometers).
Wular Lake in Kashmir is one candidate. Its volume varies with the seasons, but during the winter it's just about exactly the right size.[Unfortunately, it's shrinking. (For winter volume, see the chart on page 18 of that report.)] India is the world's second-largest tea producer, so it's also conveniently located.
Ullswater, in the UK's Lake District, is another great candidate. With a relatively stable year-round volume of about 0.23 cubic kilometers, it would be an excellent site for brewing a global cup of tea.
Of course, while neither Wular Lake or Ullswater has ever been used as a giant teakettle, something like this was—famously—attempted in my own backyard in Boston. In 1773, a group of colonists disguised as American Indians[They dressed up as American Indians to align themselves politically with the Americas—against Britain—invoking the popular European stereotype of the free and noble savage.
The Mohawk people, the actual Indians who the protesters were mimicking, mistrusted the settlers encroaching on their land, sided with the British during the subsequent war, and afterward were driven from their homes by the Americans and fled to Canada.] boarded three British ships and threw the cargo of tea—around 44 tons of it—into Boston Harbor to protest British-run tax policy.
Boston Harbor has a volume of about 0.44 cubic kilometers, which means that the "tea" brewed in 1773 would have been even more dilute than our Great Lakes tea. The harbor is also somewhat larger[The tidal range in Boston is so large (over three meters) that the harbor's volume at high tide is nearly double what it is at low.] than Wular Lake or Ullswater, so all the tea in the world would still make Boston Harbor slightly too weak.

Although it's a lot better since we built that treatment plant and stopped dumping all our raw sewage in.
There's another problem: Heat. If you wanted to make tea from a lake, such as Ullswater or Wular Lake, you'd have to heat the water up. Is that even possible?
There's clearly enough stored energy in the world to do it. After all, we presumably heat that amount of water for tea every year already; we just do it in small batches around the world.
To heat up Ullswater to 80°C[Lots of people have very strong opinions on what this temperature should be. Please direct any corrections on this matter to What-If Tea-Related Complaints Dep't, c/o Her Majesty The Queen, Buckingham Palace, London SW1A 1AA.] would take 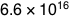 joules of energy—about 20 days worth of British electricity consumption. which is roughly what would be released if you dropped a water bottle full of antimatter in the lake.
joules of energy—about 20 days worth of British electricity consumption. which is roughly what would be released if you dropped a water bottle full of antimatter in the lake.

Not a significant source of riboflavin.
Asking Britain to go without electricity for 20 days just to fill one of their lakes with tea seems like it might be a hard sell. Fortunately, there's an easier solution.
Boiling Lake in Dominica is a volcanic lake about 60 meters across. Its temperature varies, but it's often near boiling at the edges and vigorously boiling in the center. Measuring the depth of the lake is difficult, so it's hard to get an estimate of the total volume.

The fact that it seems to boil away sometimes doesn't help.
Frying Pan Lake in New Zealand, on the other hand, is the largest hot lake in the world. It has a volume of about 200,000 m3, and an average temperature of around 50°C—not quite hot enough for tea, but much closer than Ullswater or Wular Lake.
New Zealanders consume about 600 grams of tea per person,[Kerryn Pollock. 'Tea, coffee and soft drinks', Te Ara - the Encyclopedia of New Zealand, updated 15-Jul-13] for a total of 2,700 tons of tea. If they waited until Frying Pan Lake got particularly hot, then dunked it all in at once ...
We are making a good decision by doing this thing we read on a blog. We are going to have so much tea.
... they could brew a year's worth of tea in minutes.
we went on trying foods and making plans
What if every virus in the world were collected into one area? How much volume would they take up and what would they look like?
Dave
It would be a huge pile, but human viruses would make up only a tiny fraction of it.
HIV, the virus that causes AIDS, has killed tens of millions of people worldwide, and over 30 million people are currently living with HIV. The number of copies of the virus carried in someone's blood can vary dramatically,[Data on viral load—the number of copies of the virus per mL of blood—can be found in this paper.] but across all the people in the world, there probably exists about a spoonful worth of HIV.

You should wash that spoon before you use it again.
The typical healthy human body contains about 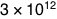 viruses. This is actually not as many as you might expect; by volume, humans are apparently a less friendly environment for viruses than, say, soil.[An area of wetlands in Delaware contains something like four billion viruses per mL of soil, in case you were looking for a fun vacation destination.]
viruses. This is actually not as many as you might expect; by volume, humans are apparently a less friendly environment for viruses than, say, soil.[An area of wetlands in Delaware contains something like four billion viruses per mL of soil, in case you were looking for a fun vacation destination.]
If you gathered together all the viruses in all the humans in the world, they would fill about ten oil drums:

So the world currently has about a 200,000,000,000:1 oil reserve:human virus ratio. I'm sure this number has some economic significance.
These 10 barrels only represent a tiny portion of the global virus community. Most of the world's viruses aren't found in humans. They're found in the sea.
Seawater is full of microorganisms, and we've recently learned that those microorganisms are preyed on by viruses in a big way. Every day, about one in five living cells in the ocean is killed by a virus.[Marine viruses—major players in the global ecosystem] These viruses are found from the surface of the ocean down to the depths.[Oddly, as you go further offshore and further down, the concentration of viruses doesn't decrease as much as the concentration of bacteria, so the virus-to-bacteria ratio is higher in the deep oceans than near the shore. ] Because the sea is so big,[Citation: Go and look at the sea. It's big.] it contains a staggering number of viruses.
If you piled up all these viruses—more than 1030 of them—in one place, they would be the size of a small mountain.
It would be a little smaller than Mount Royal in Montreal.
It's hard to say exactly what the virus mountain would look like, but it would probably resemble something in between pus and meat slurry.[Blame Dave—he's the one who asked.] Regardless of its exact appearance, it would almost certainly be disgusting.
The CDC recommends that to avoid infection, you should pour globs of pure virus into the crook of your arm instead of directly onto your hand.
The pile wouldn't stay mountain-shaped for long, any more than a mountain of any organic secretion would.[If you don't believe me, try building a mountain of earwax or snot. You'll find you can't make it higher than a few inches before your friends and family show up and sit you down for a talk.] To avoid a gigantic flood, it might be better to collect them into some kind of container.
MetLife Stadium, host of Super Bowl XLVIII, has a volume of about 1.5 million cubic meters. Earth's viruses could fill the stadium about 150 times over.
So if you watch the Super Bowl, take a moment to picture all the players floating, suspended, in a sea of yellowish-white secretions.

Belichick has his revenge.
Enjoy the game!
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
Is there any way to fire a gun so that the bullet flies through the air and can then be safely caught by hand? e.g. shooter is at sea level and catcher is up a mountain at the extreme range of the gun.
Ed Hui, London
Yes.
The "bullet catch" is a common magic trick in which a magician appears to catch a fired bullet in mid-flight—often between their teeth. This an illusion, of course; it's not possible to catch a bullet like that.[This was confirmed by Mythbusters in episode 4 of Season 4.]
But under the right conditions, you could catch a bullet. It would just take a lot of patience.[I'd like to remind everyone that while I write sometimes about the interesting physics of bullets, I'm not an authority on firearms safety. I was raised Quaker; I've never held a gun, much less fired one.]
A bullet fired straight up would eventually reach a maximum height.[Don't do this. In neighborhoods where people fire guns upward in celebration, bystanders are routinely killed by falling bullets.] It probably wouldn't stop completely; more likely, it would be drifting sideways at a couple meters per second. At that speed, as long as you were in the right place at the right time, you could snatch it out of the air.
If someone fired a bullet upward ...

Goodnight, Moon.
... and you were hanging out in a hot-air balloon directly above the firing range ...

Hmm. For every bullet I catch, I'll need to drop a tiny sandbag.
... it's possible that you could reach out and snag the bullet at the apex of its flight.
If you succeeded, you might notice something odd: In addition to being hot, the bullet would be spinning. It would have lost its upward momentum, but not its rotational momentum; it would still have the spin given to it by the barrel of the gun.
(We're in the northern hemisphere.)
This effect can be seen, dramatically, when a bullet is fired at ice.[Floor water.] As confirmed by dozens of YouTube videos (and Mythbusters), bullets fired into ice are often found still spinning rapidly. You'd have to grab the bullet firmly; otherwise, it might jump out of your hand.
If you don't have a balloon, you could potentially make this work from a mountain peak. Mount Thor, which you may remember from question #51, features a vertical drop of 1,250 meters. According to ballistics lab Close Focus Research, this is almost exactly how high a .22 Long Rifle bullet will fly if fired directly upward.[Close Focus Research, Maximum Altitude For Bullets Fired Vertically]

Oh, never mind, whoever was shooting just fell into the cotton candy pit.
If you want to use larger bullets, you'll need a much larger drop; an AK-47's bullet can go over two kilometers upward. There are no purely vertical cliffs that are that tall, so you'd need to fire the bullet at an angle, and it would have significant sideways speed at the top of its arc. However, a suitably tough baseball glove might be able to snag it.[In fact, according to Rifle Magazine, a gun writer once claimed that at a thousand yards, he could catch ordinary rifle bullets with a baseball glove. Of course, he was being figurative—you wouldn't see the bullet coming, so you'd be just as likely to catch it with your face as with your glove.]
In any of these scenarios, you'd have to get extraordinarily lucky. Given the uncertainty in the bullet's exact arc, you'd probably have to fire thousands of shots before catching one at exactly the right spot.
And by that point, you may find you've attracted some attention.

He gave my scarecrow friend a prestigious degree that turned out to be TOTALLY USELESS for finding a job!
we wanted to see the world, israel, egypt, india, laos, malaysia, nepal, tunisia
Astrophysicists are always saying things like "This mission to this comet is equivalent to throwing a baseball from New York and hitting a particular window in San Francisco." Are they really equivalent?
Tom Foster
No; the baseball thing is much harder.
How are you even supposed to throw this thing?
To throw something from New York to LA, you have to lob it out of the atmosphere like an ICBM.[Launched by New York at LA, as I'm sure happens now and then.]
Unfortunately, baseballs are too small to punch through the atmosphere. No matter how fast they're going, they'll wind up stopping before they make it to space. If you wanted to hit a window in LA with a baseball, you'd have better luck throwing it at a plane and hoping it gets lodged in the landing gear during takeoff.
The comet-visiting spacecraft Tom's astrophysicists are referring to is probably Rosetta, which is about to orbit the comet 67P/Churyumov–Gerasimenko and send a lander down to its surface.
Note: 67P/Churyumov–Gerasimenko is a mouthful, so for the rest of this article I'm just going to call the comet "Kevin".
Rosetta is currently about to arrive at Kevin, and is about 780 million kilometers from Earth. It's taken a roundabout route:
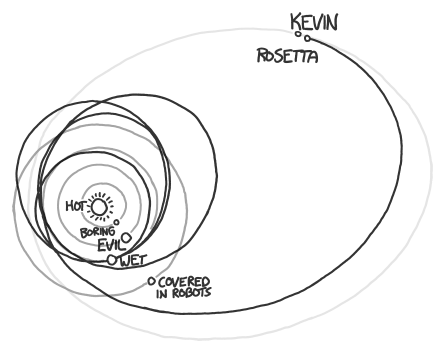
Rosetta got gravitational assists from several flybys of Earth and one of Mars, flew past two asteroids, and—in a maneuver that still has some at ESA confused—became the first spacecraft to do a flyby of itself.
Kevin, Rosetta's target, is about 4 km wide. Since it's 780 million kilometers away. If it were as far away as San Francisco is from New York, the target would be two centimeters wide—even more impressive than the statistic Tom quoted.
So Rosetta hitting its target is like throwing an object from New York and having it hit a particular key[Tilde, if you're curious.] on a keyboard in San Francisco.
I TOLD you to aim for SAVE!
It's not a fair comparison, but you gotta admit, it sounds pretty precise. I once heard an account from someone who worked on the Cassini-Huygens mission, where one of the designers pointed out that their spacecraft traveled to a target a billion kilometers away, and arrived within something like a second and a half of the scheduled time.[Despite searching, I've been unable to track down this interview. If you see it, let me know!]
On the other hand, we could make less flattering comparisons.
Take remote surgery. If a surgeon in New York uses a remote surgery robot in San Francisco to do eye surgery, and the robot aims for the patient's eye with the precision of Rosetta's approach, it will point its laser somewhere around here:
At least it'll help clear my sinuses.
However this isn't a fair comparison either. Both Rosetta and our laser surgeon[I really hope that's what this job is called] will refine their movements as they make their final approaches, achieving very high precision.
When it comes down to it, the two tasks—remote surgery and remote probe-landing—are probably about equally precise, in a distance sense.
Which brings me to something a little different with which I'd like to end this article: A question for you to try to answer. Namely:
Would you rather bet a million dollars on a spacecraft landing engineer's ability to successfully perform eye surgery, or an eye surgeon's ability to land a probe on a comet?I haven't been able to decide.
But don't worry; that's a rare complication, only happening in one in every 20 or 30 procedures.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
If you made a beach using grains the proportionate size of the stars in the Milky Way, what would that beach look like?
Jeff Wartes
Sand is interesting.[Citation needed]
"Are there more grains of sand than stars in the sky?" is a popular question which has been tackled by many people. The upshot is that there are probably more stars in the visible universe than grains of sand on all of Earth's beaches.
When people do those calculations, they often dig up some good data on the number of stars, then do some hand-waving about sand grain size to come up with a number for the sand grains on Earth.[From a practical point of view, geology and soil science are more complicated than astrophysics.] We're not going to tackle that issue today, but to answer Jeff's question, we do need to figure out what the deal with sand is.["i like sand because i don't really know what it is and there's so many of it"
—@darth__mouth] Specifically, we need to have some idea of what grain sizes correspond to clay, silt, fine sand, coarse sand, and gravel, so we can understand how our galaxy would look and feel if it were a beach.[Instead of just containing a bunch of them.]
Fortunately, there's a wonderful chart by the US Geologic Survey that answers all these questions and more. For some reason, I find this chart very satisfying—it's like the erosion geology edition of the electromagnetic spectrum chart.
According to surveys of sand,[There are apparently lots of them.] the grains found on beaches tend to run from 0.2mm to 0.5mm (with the finest layers on top). This corresponds to medium-to-coarse sand in the chart. The individual grains are about this big:
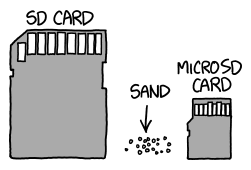
(sandisk)
If we assume the Sun corresponds to a typical sand grain, then multiply by the number of stars in the galaxy, we come up with a large sandbox worth of sand.[I mean, you come up with a bunch of numbers, but imagination turns them into a sandbox.]
However, this is wrong. The reason: Stars aren't all the same size.
There are a number of widely-circulated YouTube videos comparing star sizes. They do a good job of getting across just how staggeringly large some stars are. Although it's easy to get lost in the videos and lose track of scale, it's clear that some of the grains in our sandbox universe would be more like boulders.
Here's how the main-sequence[The stars in the main part of their fuel-burning lifecycle.] star-sand grains look:

These stars are all technically called 'dwarf' stars. Astronomers could learn a thing or two about straightforward nomenclature from the sand-grain geologists.
They mostly fall into the "sand" category, though the larger Daft Punk stars cross the line into "granules" or "small pebbles".
However, that's just the main sequence stars. Dying stars get much, much bigger.
They're almost as big as SD cards!
When a star runs out of fuel, it expands into a red giant. Even ordinary stars can produce huge red giants, but when a star that's already massive enters this phase, it can become a true monster. These red supergiants are the largest stars in the universe.

I have a vague feeling that I shouldn't be looking directly at this rock.
These beachball-sized sand stars would be rare, but the grape-sized and baseball-sized red giants are relatively common. While they're not nearly as abundant as Sun-like stars or red dwarfs, their huge volume means that they'd constitute the bulk of our sand. We would have a large sandbox worth of grains ... along with a field of gravel that went on for miles.

This beach sucks.
The little sand patch would contain 99% of the pile's individual grains, but less than 1% of its total volume. Our Sun isn't a grain of sand on a soft galactic beach; instead, the Milky Way is a field of boulders with some sand in between.
But, as with the real Earth seashore, it's the rare little stretches of sand between the rocks where all the fun seems to happen.
Just to be clear, this image does not update every hour.
and we wanted to find a community in spain
Has humanity produced enough paint to cover the entire land area of the Earth?
—Josh (Bolton, MA)
This answer is pretty straightforward. We can look up the size of the world's paint industry, extrapolate backward to figure out the total amount of paint produced. We'd also need to make some assumptions about how we're painting the ground. Note: When we get to the Sahara desert, I recommend not using a brush.

I hear a film director actually did this once, in the days before digital color correction.
But first, let's think about different ways we might come up with a guess for what the answer will be. In this kind of thinking—often called Fermi estimation—all that matters is getting in the right ballpark; that is, the answer should have about the right number of digits. In Fermi estimation, you can round[Using the formula  , meaning that 3 rounds to 1 and 4 rounds to 10.] all your answers to the nearest order of magnitude:
, meaning that 3 rounds to 1 and 4 rounds to 10.] all your answers to the nearest order of magnitude:

Legs per cat: 10
Let's suppose that, on average, everyone in the world is responsible for the existence of two rooms, and they're both painted. My living room has about 50 square meters of paintable area, and two of those would be 100 square meters. 7.15 billion people times 100 square meters per person is a little under a trillion square meters—an area smaller than Egypt.
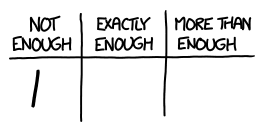
My vote for Lizard People was thrown out.
Let's make a wild guess that, on average, one person out of every thousand spends their working life painting things. If I assume it would take me three hours to paint the room I'm in,[This is probably optimistic, especially if there's an internet connection in the room.] and 100 billion people have ever lived, and each of them spent 30 years painting things for 8 hours a day, we come up with 150 trillion square meters ... just about exactly the land area of the Earth.
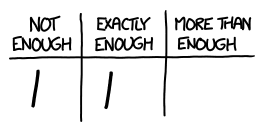
It's a tie!
How much paint does it take to paint a house? I'm not enough of an adult to have any idea, so let's take another Fermi guess.
Based on my impressions from walking down the aisles, home improvement stores stock about as many light bulbs as cans of paint. A normal house might have about 20 light bulbs, so let's assume a house needs about 20 gallons of paint.[These are very rough estimates.] Sure, that sounds about right.
The average US home costs about \$200,000. Assuming each gallon of paint covers about 300 square feet, that's a square meter of paint per \$300 of real estate. I vaguely remember that the world's real estate has a combined value of something like \$100 trillion,[Citation: This really boring dream I had once.] which suggests there's about 300 billion square meters of paint on the world's real estate. That's about one New Mexico.
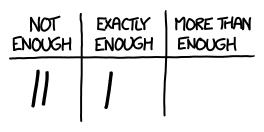
'Lizard People' demands a recount.
Of course, both of the building-related guesses could be overestimates (lots of buildings are not painted) or underestimates (lots of things that are not buildings[EXAMPLES OF THINGS THAT ARE NOT BUILDINGS: Ducks, M&Ms, cars, the Sun, cuttlefish, microchips, Macklemore, lightning, goat blood, zeppelins, tapeworms, pickle jars, those sticks you use to toast marshmallows, alligators, tuning forks, minotaurs, Perseid meteors, ballots, crude oil, sponsored tweets, and catapults that throw handfuls of engagement rings.] are painted) But from these wild Fermi estimates, my guess would be that there probably isn't enough paint to cover all the land.
So, how did Fermi do?
According to the report The State of the Global Coatings Industry, the world produced 34 billion liters of paints and coatings in 2012.
There's a neat trick that can help us here. If some quantity—say, the world economy—has been growing for a while at an annual rate of n—say, 3% (0.03)—then the most recent year's share of the whole total so far is 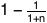 , and the whole total so far is the most recent year's amount times
, and the whole total so far is the most recent year's amount times 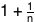 .
.
If we assume paint production has, in recent decades, followed the economy and grown at about 3% per year, that means the total amount of paint produced equals the current yearly production times 34.[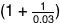 ] That comes out to a little over a trillion liters of paint. At 30 square meters per gallon,["Square meters per gallon" is a pretty obnoxious unit, but I think it's not quite as bad as acre-foot (a foot by a chain by a furlong), which is an actual unit used in technical papers I was trying to read this week.] that's enough to cover 9 trillion square meters—about the area of the United States.
] That comes out to a little over a trillion liters of paint. At 30 square meters per gallon,["Square meters per gallon" is a pretty obnoxious unit, but I think it's not quite as bad as acre-foot (a foot by a chain by a furlong), which is an actual unit used in technical papers I was trying to read this week.] that's enough to cover 9 trillion square meters—about the area of the United States.
So the answer is no; there's not enough paint to cover the Earth's land, and—at this rate—probably won't be enough until the year 2100.
Score one for Fermi estimation.

Two movies called Star Trek, one called Star Trek II, one called Star Trek III, and a BUNCH of movies called Star Trek X.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
Assuming that you have a spaceship in orbit around the Earth, could you propel your ship to speeds exceeding escape velocity by hitting golf balls in the other direction? If so, how many golf balls would be required to reach the Moon?
—Dan (Kanata, Ontario)
It depends how good your swing is.
That sounds glib, but it's sort of true. The answer to this question hinges on exactly how fast you can hit a golf ball.
Sometimes, exact numbers don't matter that much. If my baseball, car, dog, or Zamboni goes a little faster than yours,[$20 says they will!] it will go a little farther. But that's not how it works in rocket golf. The design of our spaceship turns out to involve an equation where the speed of the golf ball is in the exponent. That means a small change in speed can make a big difference.
The equation in question—which might be my favorite in all of physics—the Tsiolkovsky rocket equation:

This equation comes up a lot in What If calculations. I like it both because it says something fundamental about our ability to explore the universe, and because you can use it to get really good at Kerbal Space Program.
With some rearranging, the equation can help us figure out how much of our ship's weight has to be golf balls:
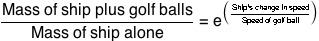
Someone who, like me, has never been golfing before, might—after swinging and missing a few times—manage to hit the ball at 120 mph (50 m/s).[See Trackman's page on ball speed] To get to the Moon from low Earth orbit, you would need enough fuel to add 5,300 m/s to your ship's speed. By putting those numbers into the rocket equation, we can find out how large a sack of golf balls would have to be for the average golfer to reach the Moon. If we plug it in to Wolfram|Alpha ...
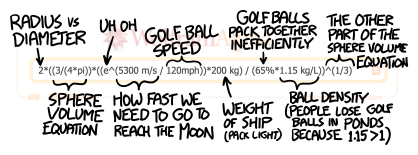
I didn't end up getting banned this time.
... we find that the bag of golf balls will have to be just about exactly 100 billion miles in diameter. That's much, much bigger than our Solar System.[As a Fermi rule of thumb, planets in the inner Solar System are 100 million kilometers away and planets in the outer Solar System are a billion kilometers away. Or miles; either one works.]

Not pictured: Pretty much anything that isn't golf balls.
It would also promptly and violently collapse into a black hole.
Fortunately, we should be able to avert that disaster by making relatively small changes to the "120" in that equation. If we increase the golf ball's speed from 120 mph to 150, it shrinks the answer dramatically, and the required number of golf balls would fit snugly between the Sun and Mars. Still too big to avoid a catastrophic collapse, but we're getting somewhere.
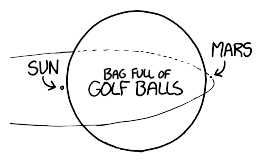
Not pictured: Earth, which is in the bag of golf balls.
Tiger Woods can hit a golf ball at about 180 mph, which means that if he were powering our spaceship, the bag of golf balls would be only twice the diameter of the Sun!

I think it's tennis balls.
According to the Guinness Book of World Records, the record for fastest golf drive is 211 mph, set by Maurice Allen in 2012. This corresponds to a bag of golf balls only 100,000 kilometers across—smaller than Jupiter, but still (obviously) not practical.
However, golfer Ryan Winther claims to have beaten this record, though without Guinness observers there.[And, obviously, it doesn't count unless it's overseen by people from a beer company. If you want to set a world record, hit a golf ball at a radar gun and get it certified by the Mike's Hard Lemonade people.] His ball speed was measured by something called the "Titleist Performance Institute" to be 226.7 mph, and he claims a personal best of 237 mph. If he could consistently hit 237 mph, we could shrink our fuel container down to the size of Earth[Although it would still be large enough to partially collapse under its own gravity, similar to what happened to the mole of moles.]

Golf courses occupy about 1/20,000th of the world's total land area. On a desk globe, they would be about this big: o
This still wouldn't work; even in a high orbit, the massive tides from your ship—which is much more massive than the Moon—would be highly disruptive.
We could probably shrink the fuel tank further by using "illegal" equipment. There are Superball-style balls and "trampoline face" clubs which can hit much farther, and which would not be permitted in tournament play.[On the other hand, we're talking about a sport that brought whites-only clubs with it into the 21st century, and Agusta, host of the Masters, admitted its first woman in 2012. So maybe we shouldn't worry too much about their traditional rules.] A hypothetical 270 mph drive would allow a fuel tank the size of the Moon.
At this point, why are we even using a club?
According to research from the US Air Force Academy and BTG Research,[Oddly, both researchers have the name "Courtney". There are probably about 200,000 people in the US named Courtney (first or last); maybe we should recruit them to all build potato cannons.] a potato cannon fueled by acetylene can launch a potato at 140 m/s (310 mph). If it were capable of launching golf balls at that speed,[We're not factoring in the weight of the acetylene—but then again, we also weren't factoring in the weight of the hamburgers the golfer would need to eat to keep hitting those drives.] our ship would have a diameter of only 150 miles!

LOOK OUT SPACE STATION AHEA-- ... uh, never mind. Oops.
There's the small problem that manufacturing that many golf balls would cost quintillions of dollars. You could bring the size down further by making the potato cannon more and more powerful and efficient, but at that point you're simply building a rocket.
And the potato cannon scenario has an extra perk. If you somehow made the balls durable enough to survive atmospheric entry, and you set up your maneuver so the ejected golf balls covered the middle latitudes evenly, then over the course of this maneuver you would be statistically likely to hit a hole-in-one ... at every golf course in the world.
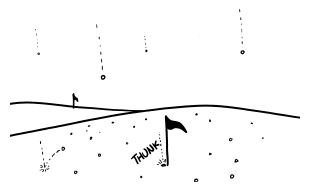
The ones that landed in the water would have enough volume to raise the water level substantially—except on the Dead Sea, where they'd float on the surface.
we were torn between choices, and shredded by the shittiness of ecosea
In terms of human-made objects, has Voyager 1 travelled the farthest distance? It's certainly the farthest from Earth we know about. But what about the edge of ultracentrifuges, or generator turbines that have been running for years, for example?
Matt Russell
Spacecraft go a lot faster than centrifuges.[With a few exceptions, as you'll see in the next footnote.] Spacecraft travel at speeds measured in kilometers per second, and they maintain those speeds constantly. Machine parts rarely move faster than a few hundred meters per second, which means that they probably won't catch up.
But the precise answer to this question depends on what reference frame we're using. Let's go through a few of the options:
Measured relative to the Sun
As far as moving through the Solar System goes, Voyager 1 is one of the slowest manmade objects.[It's not the very slowest—that title might belong to the Galileo spacecraft. On September 6th, 1996 at 10:57 (UT), Galileo's speed relative to the Sun dropped to 276 meters per second (618 mph), making it possibly the slowest manmade object in Solar System history.] It's moving at an average speed of about 16 km/s, which is barely half of the Earth's orbital speed around the Sun.
It might seem a little intuitively weird that Voyager 1, which went fast enough to escape the Solar System, is going slower than Earth, which didn't. But it makes more sense if you think of the Solar System as a furious whirlpool with the planets caught in it. Voyager 1 (partly by pushing off those planets) managed to go fast enough that it was flung from the whirlpool, and is now drifting sedately across the water's surface.[And will continue doing so forever, unless we go get it.]
In other words, every 1977 Plymouth Voyager van has traveled farther than Voyager 1.
And more people have had sex in Plymouth Voyagers than Voyager spacecraft, unless NASA JPL is a wilder place than I thought.
The longest-traveled manmade objects, by this measure, aren't spacecraft at all—they're whatever objects have been on the Earth the longest, and have thus traveled the farthest around the sun. The first known surviving manmade objects are 2.6-million-year-old stone tools from Ethiopia, which have traveled a total of about 250 light-years.
By comparison, the most well-traveled space probe (possibly the defunct Mariner 10, which has been in a relatively tight loop around the Sun for decades) has only traveled a couple of light-days, and the Voyagers have barely logged a dozen light-hours.
Fermi estimation problem for anthropologists: Which is more likely to have struck and killed someone: A random Oldowan stone tool, a random Voyager spacecraft, or a random 77 Plymouth Voyager? I'm guessing it's not the middle one. (Unless there was an accident during assembly.)
Measured relative to the Earth
By this measure, the Ethiopian stone tools win again. They were crafted relatively close to the Equator, so they've spent their millions of years traveling at about 460 meters per second as the Earth rotates, racking up 4 light-years on their odometers.
Speed over the Earth's surface
This rotating frame of reference effectively zeroes out the odometer on the stone tools. It also means that spacecraft far away from the Earth are sort of a weird case, since they "move" over the Earth's surface at the speed at which the planet spins. But that turns out not to matter, because the winner in this category is Vanguard 1, which has been in orbit since 1958, logging about 8.888 billion kilometers over the surface.
Normal speed, without any weird space stuff or Earth rotation or whatever
First, let's think about things that travel in a straight line. There are a lot of those, including a 1966 Volvo in Long Island which has driven 3 million miles. There are other vehicles that travel long distances—long-haul airliners, for example—but the winner in this category might actually be a human.
United Airlines flight attendant Ron Akana traveled about 20 million miles over his 63-year career, which might be the most of any human; even someone who sailed on steamships their whole life would have a hard time traveling that far.[It's not enough to beat the astronauts, though; cosmonaut Valeri Polyakov spent over a year in orbit, which adds up to a life odometer 10 times longer than Ron Akana's.][You could argue that he doesn't qualify as a human-made object, but he was certainly made. And anyway, he may have an object he carried with him for most of those flights. The article mentions he was married, so perhaps his wedding ring qualifies.]
Some train cars—or things used in trains—might push the total a little higher, but it seems unlikely that any kind of vehicle has traveled 100 million miles.
Things that rotate are a different matter.
We'll start with hard drive platters.[If you're reading this in the future, hard drive platters were these things that ... oh, never mind, it's not important.] A 3.5" hard drive at 7200 rpm is moving at about 80 mph. Drives have a limited lifetime—especially if they're run constantly—but it's easy to imagine the edge of a platter somewhere logging millions of miles before it died.
The energy industry has some good candidates. The tips of wind turbines can move faster than cars, and turbines can run for decades. Even if the wind isn't constant, some of them have probably traveled tens of millions of miles.
The discs used in flywheel energy storage are even more promising than wind turbines. Flywheels are designed to spin (usually in a vacuum) for decades at a time, with rotor speeds above Mach 1. There's probably a flywheel somewhere whose rotor rim has traveled a nine-digit number of miles.[Hundreds of millions.]
The edges of centrifuges, especially those used for uranium enrichment, can travel even faster—in fact, they push the very limits of how fast material can rotate.
There's an absolute limit to how fast anything can spin without breaking apart. For the very strongest materials, like carbon fiber and kevlar, the top speed that the outer edge of a spinning cylinder can travel is between 1 and 2 kilometers per second.[Units are weird: The maximum speed the edge of a cylinder of a given material can rotate is equal to the square root of its specific tensile strength (tensile strength over density).] If we assume those materials and the precision techniques to produce them have only existed for the last half-century, then the greatest distance a centrifuge could possibly have traveled is about a billion kilometers—and the actual record is almost certainly much less. This is why uranium enrichment involves titanium centrifuges; the uranium needs to be spun very fast, and only specialized materials are strong enough to hold together at those speeds.
All in all, uranium enrichment centrifuges seem like a likely winner, with total lifetime odometer that might push into the hundreds of millions of miles.
How fast?
So, exactly how far has the longest-operating centrifuge traveled?

¯\(°_o)/¯
I don't know.
Normally I don't give up like this, but if I had a way to estimate exactly how fast and for how long the labs in different countries have been spinning their uranium enrichment centrifuges, I would probably not be blogging about it here.

I also have many facts about meteors, tornadoes, and ice.
In any case, the centrifuges have logged far less total distance than many manmade objects, including (by various measures) the Ethiopian stone tools, the ISS, Mariner 10, and the Voyagers.
And for what it's worth, based on the "every 3,000 miles" rule, the Voyagers have missed several million oil changes each.

That's totally an industry scam. NASA shouldn't change Voyager's oil more than every 5 or 6 thousand miles.
Maybe it's best that we just leave them.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
I've occasionally seen "radar enforced" on speed limit signs, and I can't help but ask: How intense would radio waves have to be to stop a car from going over the speed limit, and what would happen if this were attempted?
—joausc
Radio waves exert force on things.
Not a lot of force. The average cell phone transmitter exerts about a billionth of a newton of pressure on its surroundings. That means that it would take several trillion cell phones to collectively levitate a snowflake; the pressure from one phone wouldn't even measurably slow it down.

Under the right circumstances, the convection from the phone's heat could probably deflect a snowflake.
If the phone did put out enough energy to levitate a snowflake by radiation pressure, the power flowing through the snowflake (a few kilowatts) would quickly cause the snowflake to become a raindrop, which would quickly become water vapor, which would quickly become the least of your problems.

I thought our plan had unlimited snowflake levitation.
The fate of the snowflake hints at what kinds of problems our car will encounter.
If you want to slow down a one-ton car by radiation pressure, your radar gun would need to deliver about two trillion joules worth of radiation—the energy of a small nuclear weapon.[The formula for figuring out that amount out is simple: The energy required is equal to the desired change in speed (say, 20 mph) times the mass of the car times the speed of light.] The radar gun would need to emit even more energy than that, since not all of the radiation will be absorbed (or reflected) by the car.[The fact that some of it is reflected makes things easier, since that doubles the momentum delivered by the radiation. This is why simple solar sails are white and not black. For more on radar reflectivity of materials, you can check out one of the worst scanned PDFs I've ever seen.]
Your radar gun would also vaporize the car. This is a problem, in one sense, but it's also a solution. Even if most of the energy is reflected, the portion that was absorbed would convert the materials in the car into gas or plasma. The expanding cloud would exert a lot more pressure on the car than the radiation itself.[This process, called ablation, is also what got rid of the Moon in the What If #13.] This is convenient—it means that we wouldn't need nearly as much energy to stop the car as we would using radiation pressure alone.
There are even simpler ways to slow down a car with radiation. For example, you could aim a radiation beam at the tires and melt them, or use the electromagnetic radiation to knock out the car's electrical systems. Or just use a laser pointer to blind the driver and hope they reflexively slow down.
Of course, you don't need any of those things. If your goal is to slow down the car—rather than to catch speeders—your radar gun doesn't need any power. You can just stand by the side of the road next to a police car holding a fake radar gun.

He's been waiting his whole life for someone to ask "what's your sign", but nobody has.
In the end, a radar gun capable of slowing cars through radiation pressure would be roughly equivalent to a nuclear weapon, and using nuclear strikes in response to traffic violations is probably overkill. It would work, in the literal sense, but it would also destroy the offender, car, police officer, road, and all other traffic for miles around.[It would also cause fragments of the driver to violate the speed limit in all directions at once.]
Of course, maybe using the apocalyptic radar gun wouldn't be necessary; just the threat of a nuclear strike against drivers would probably deter speeding.
Come to think of it, maybe that's what those other signs you sometimes see are hinting at.

Protip for potential speeders: Since the B-2's stealth technology incorporates radar-absorbing materials, it's particularly vulnerable to radar gun death rays.
we almost split
How much CO2 is contained in the world's stock of bottled fizzy drinks? How much soda would be needed to bring atmospheric CO2 back to preindustrial levels?
Brandon Seah
For most of the history of civilization, there were about 270 parts per million of carbon dioxide in the atmosphere. In the last hundred years, industrial activity has pushed that number up to 400 parts per million.
One "part per million" of CO2 weighs about 7.8 billion tons. A can of soda contains in the neighborhood of 2.2 grams of CO2, so you would need about 450 quadrillion cans of soda. That's enough to cover the Earth's land with ten layers of cans.
Mesosphere, asthenosphere, lithosphere, sodasphere
There's clearly not enough room to do this. Even if we stacked the cans up to the edge of space,[I don't have any hard numbers, but my guess would be that you could probably stack supermarket soda six-pack crates a few hundred meters high before the bottom layer ruptures.] they'd still take up an area the size of Rhode Island.[We shouldn't actually try it, given what happened last time.]
We'd need to add even more cans to keep up with ongoing emissions. We're currently increasing the atmosphere's CO2 concentration by an average of 2 parts per million each year:
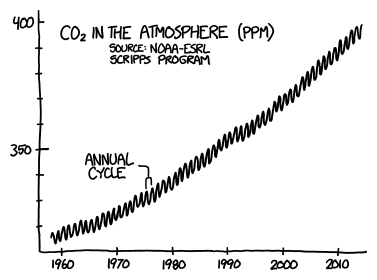
If you squint at some of these graphs, you can see the effect of the fall of the Soviet Union due to abrupt industrial and land use changes.
At that rate, we'd need to add one can of soda per person every 30 seconds, which is about 10,000 times the current consumption rate.[The global average is one can per person every 5 days. In the US, the average is one every 18 hours.] That would add a new layer of cans to the ground every 6[I originally had the wrong number here; thank you to Paulina for catching it!] years or so.
This layer of cans would get pretty annoying.

Following the resurfacing, that soda/coke/pop dialect map will come to define our national political divisions.
Are there any ways out of this predicament?
In some areas, you can turn in soda cans for recycling and receive a small amount of money; in Massachusetts, where I live, it's 5 cents. If you collected one year's worth of soda cans—instead of layering them across the Earth's surface—and emptied them out, you could redeem them for $372 trillion.
With that much money, you could simply buy the world's current reserves[Source: xkcd.com/980, bottom right.] of coal, oil, and natural gas—the source of the whole problem.
Then, you put it all back in the ground and leave it there.
You're never, ever gonna get your wish.
Problem solved.
you are awesome, the most beautiful person i have ever met and you make me happy everyday i spend with you
How far would a tungsten countertop descend if I dropped it into the Sun?
Michael Leuchtenburg
Not very far.
With its high melting point, tungsten is a good[Except that the word "good" implies that you have some kind of goal you're working toward, which—given how strange the thing you're doing is—I'm not sure about.] choice for a sundiving countertop.
The first problem would be sunlight. As the countertop approached the Sun, it would heat up. Tungsten has the highest melting point of any element, but the Sun is one of the meltiest things in the Solar System. When the countertop got within a couple of solar radii, it would liquify.

Assuming it's ever launched, Solar Probe Plus will get within 1/8th of Mercury's orbital distance.
If you protected it with a heat shield of some kind, or dropped it from a sundiving spaceship, it could enter the Sun's atmosphere relatively intact. In this case, some interesting physical effects would destroy it.["Some interesting physical effects would destroy it" summarizes the answers to a large percentage of the questions submitted to this blog.]
Because the Sun is so heavy, anything that falls to its surface will be accelerated to a tremendous speed by its gravity. A falling countertop would reach speeds of over 600 km/s—0.2% of the speed of light. (Our rockets can only accelerate spacecraft to 10-20 km/s.)
From the countertop's point of view, particles from the Sun's atmosphere would be slamming into it at 600 km/s. These particles would pack quite a punch.[From a particle physics point of view, the individual protons would have energy of about 2 keV.] When the countertop got within about a few thousand kilometers[I don't want another unit-related word to mentally keep track of, but it's always seemed a little weird that we don't call thousands of kilometers "megameters".] of the Sun's surface, these collisions would start delivering more energy to the countertop than the sunlight.
The collisions would fling individual tungsten atoms away from the surface—a process called sputtering. Between the sputtering and ordinary heating from the impacts, the countertop would start to absorb a lot of energy very quickly.
If the countertop were larger, it could penetrate into the Sun's photosphere—the first layer beneath the "surface"—and potentially trigger a solar flare.[For a scientific discussion of this, see the article Impacts of comets onto the Sun and coronal mass ejections. For a science fiction discussion of this, see Stephen Baxter and Arthur C. Clarke's 2005 novel Sunstorm.] But as it is, it wouldn't even make it through the Sun's atmosphere—it would be vaporized somewhere in the Sun's chromosphere.
Goodbye, faithful countertop. I'm not sure what your mission was, but I'm sure you've performed it well.
This brings us around to a key question:
Who the hell has tungsten countertops?
Sure, it has good heat tolerance. But I'd be nervous about using tungsten as a food-preparation surface.
In September of 1994, a French soldier drank wine from a rifle barrel. Fifteen minutes later, he started having seizures. He was rushed to the hospital and treated for "acute tungsten intoxication"—the first known case in medical history. He reportedly made a full recovery, although concentrations of tungsten were present in all his body tissues for weeks.
The lesson here is to use normal materials. Michael, just make your countertops out of granite and don't drop them in the Sun.
And if you're a French soldier, please just drink wine like a normal person.
Close enough.
i'm finishing this text in koh kong, you are lying in front of me, reading your book. we came back yesterday from our adventure in the montains brought back by the red cross. we went to the market this morning to try out things (fried bananas and cane juice). i feel filled with you. you are beautiful. i love you.